在这篇博文中,我们将简要介绍以下主题,为您提供机器学习的基本介绍:
- 什么是机器学习
- 训练机器学习模型
- 优化参数
- 神经网络
如果您不是专家,请不要担心 — 这篇博文所需的唯一知识是基础高中数学。
什么是机器学习?
牛津词典将机器学习定义为:“计算机从经验中学习的能力”。
机器学习的目标是提出可以学习如何基于示例数据执行特定任务的算法。举个例子:假设我们要编写一个程序来玩围棋游戏。我们可以通过手动定义如何玩游戏的规则来编写这个程序。我们可能会编写一些开局策略和决策规则——例如,从棋盘中心开具会比较好。
但是有一个问题。手动编写这些规则意味着它们会很快变得非常复杂,并且受到我们作为程序员可以想出的策略的限制。更好的解决方案是构建机器学习算法。机器学习可以根据示例和经验学习如何下围棋,就像人类一样。这就是 DeepMind 对他们的AlphaGo程序所做的,这是一种基于深度学习的机器算法,结果非常好,它战胜了(人类)围棋世界冠军。
训练机器学习模型
机器学习算法基于标记数据的示例训练模型。机器学习算法通常定义具有可调参数的模型和优化算法,如下图所示。该模型以数据 ( x )的形式接受输入,并根据输入数据及其参数生成输出 ( y )。优化算法试图找到参数的最佳组合,以便在给定示例x的情况下,模型的输出y尽可能接近预期输出。经过训练的模型将表示给定x产生输出y的特定函数f。所以:y=f(x)。
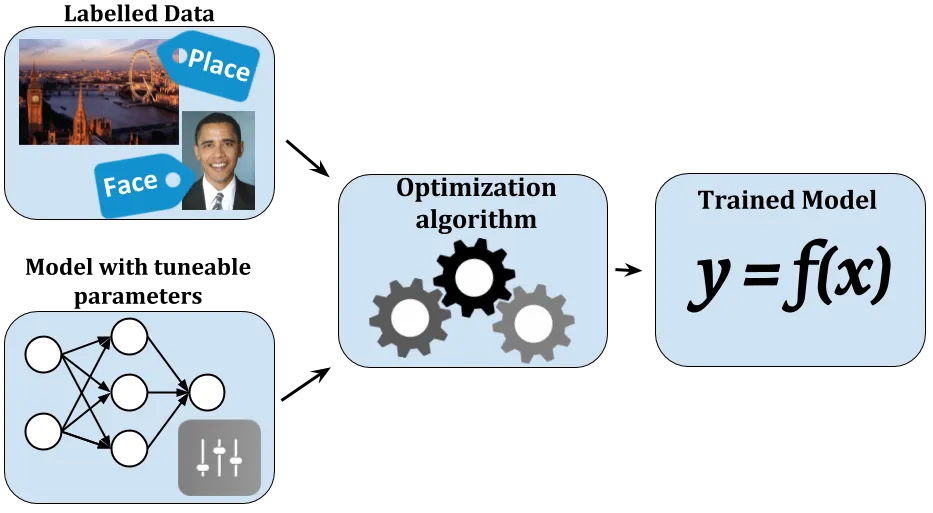
优化
有很多方法可以找到最佳参数组合,使模型f的输出y尽可能接近给定输入x的预期输出。一种方法是尝试所有可能的参数组合,然后选择能提供最佳结果的组合。如果只有有限数量的参数组合,这可能会奏效,但对于具有数千甚至数百万个参数的典型机器学习模型,这是完全不切实际的。幸运的是(并感谢 17 世纪数学家牛顿的发明),有一种更好的方法可以为某些类型的模型找到最优解, 这就是导数(通常也称为梯度)。函数的导数表示函数相对于其参数之一如何变化,并指向函数增加的方向。如果我们有一个具有参数p的函数f,那么函数f相对于参数p的变化dp的变化 df记为df(p)/ dp。
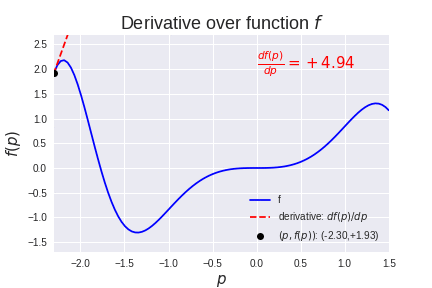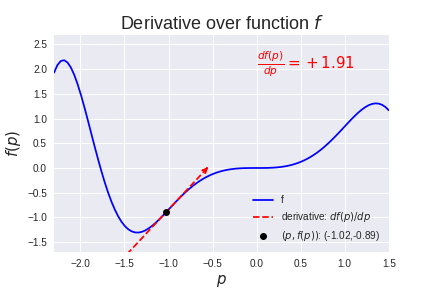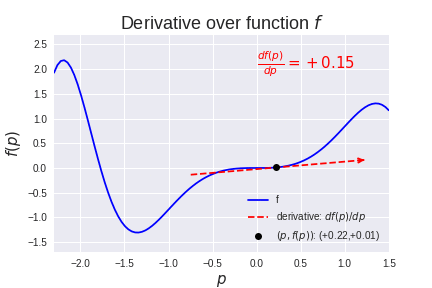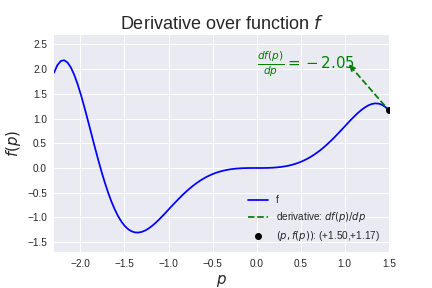
那么如何使用这个导数来让模型的优化更高效呢?假设我们有一些数据(x, t)以便输入x对应于目标t。此数据绘制如下:
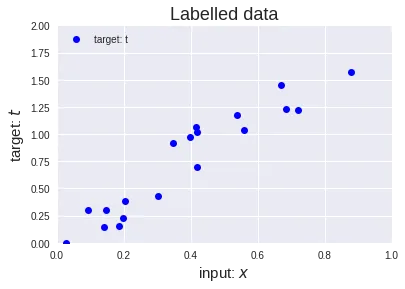
如果我们现在想要为所有给定示例创建一个模型,该模型最接近给定输入x的目标t,那么我们可以尝试通过原点拟合一条直线(这也称为线性回归)。这条直线可以用函数y=f(x)表示,其中f(x)=p⋅x其中p是模型的唯一参数(注意p表示直线的斜率)。该模型可以直观地表示为:

为了找到参数p使y=x⋅p对于所有给定的示例(x,t)都尽可能接近t,我们必须以数学方式定义“接近度”的度量。此度量也称为成本函数。此问题的典型成本函数是对所有示例(x,t)的目标t和模型输出y之间的所有绝对差值的平方求和:|ty|²。最终成本函数变为∑|t - (x⋅p)|²,其中 sigma 表示总和。因为这个例子非常简单,我们实际上可以很容易地将所有参数p的成本函数可视化:
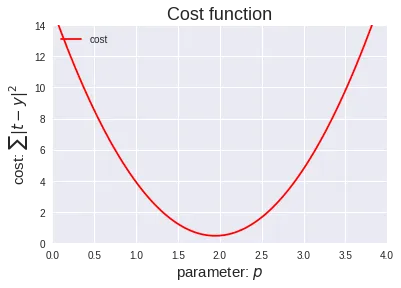
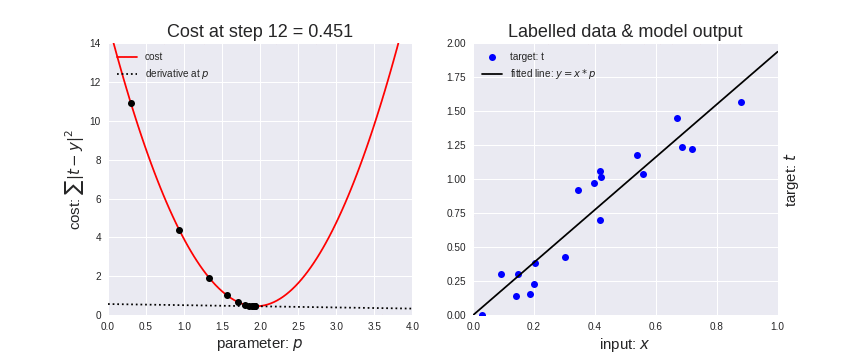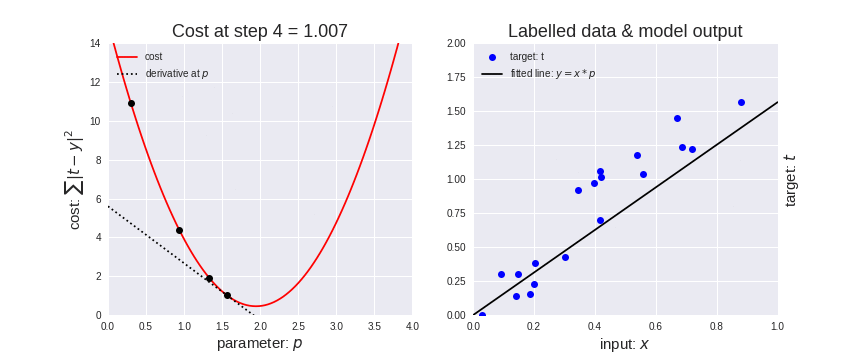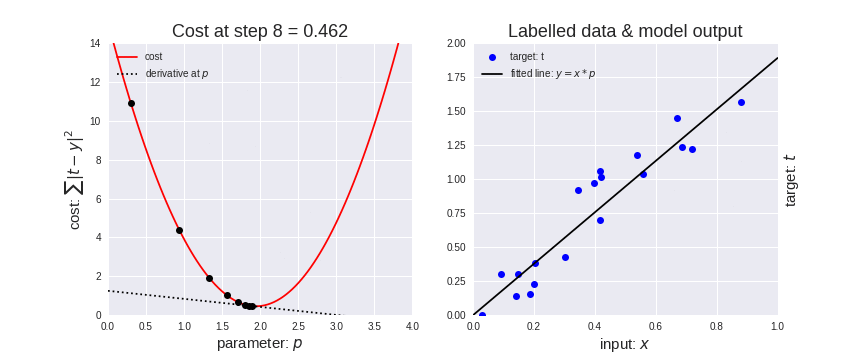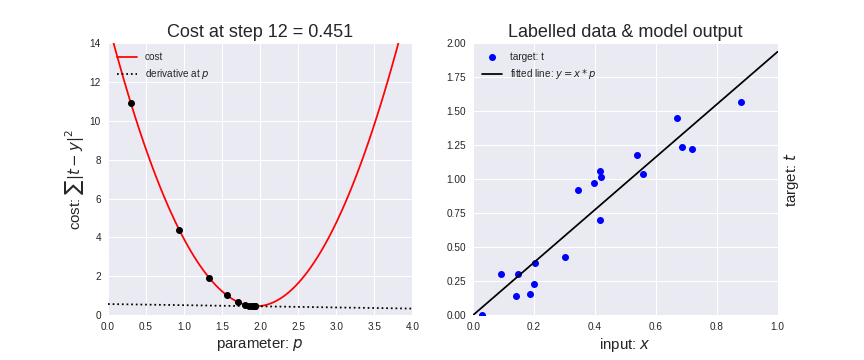
为了找到最佳参数p,我们需要最小化代价函数。请记住,我们的模型有一个参数p,接受输入x并产生输出y。我们可以将此模型写为y=x⋅p。由于成本是∑|ty|²我们可以替换y,并将成本函数写为∑|t - (x⋅p)|²。如果我们想最小化这个函数并使输出y尽可能接近目标t ,我们可以为每个输入样本(x,t)尝试所有可能的p值并选择p的值其中所有输入样本的成本总和最低。在这种情况下尝试p的所有可能值是可能的,但模型具有的参数越多,很快就会变得不可行。这就是衍生品发挥作用的地方。有了导数,我们可以简单地为p选择一个随机起始参数值,然后开始沿相反方向跟随导数以找到成本函数的最低点。这种随着导数(梯度)下降的过程也称为梯度下降。该过程如下图所示,我们从p=0.3开始并按照梯度进行 12 步,同时提高模型对数据的拟合度(右图拟合的线)。当成本不再下降太多时,我们停止拟合模型,因此找到的最终参数p为1.94,成本为0.451。请注意,最后一行比初始行更适合数据(x,t) 。
神经网络
从本质上讲,如果我们训练神经网络模型,就会发生这种情况。然而,更典型的神经网络模型由比我们的y=x⋅p模型复杂得多的函数组成。神经网络模型种类繁多,但通常它们都是可微分的,并且可以使用梯度下降法进行优化,正如我们在这篇博文中所说明的那样。
例如,用于计算机视觉的典型神经网络将由多个层组成。每层都有成百上千个参数,后面跟着一个非线性函数。在神经网络中拥有多层是“深度学习”一词的来源。在模型中使用多层的好处是每一层都可以使用在前一层中提取的信息来构建更复杂的数据表示。正因为如此,神经网络才被证明如此强大,成功训练以多种复杂模型以解决实际应用场景。关于神经网络的知识,我们会在下一篇详细介绍。











