并查集是在各个不相交集合中查找某元素存在否，可以接近常数级查找例如，图的连通性，最近公共祖先等问题。一般用森林 数组实现。

一般有2个操作，查找(find)和合并(union)

查找：从集合中查找元素x是否存在。

合并：如果2个集合不想交则可以合并操作，一般方法是高度低的合并到高度高的。

初始化每个元素都可以是一个单独的集合，然后不断引入关系来合并他们

问题引入：

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。 规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

简单地看是2个元素xy在这个庞大的关系网络中是否有是亲戚关系，每个成员都可以看做是一个元素，常规的图论做法深度搜索 代价比较大。

并查集很适合这种情况下的查找判断

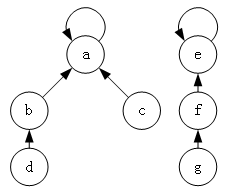
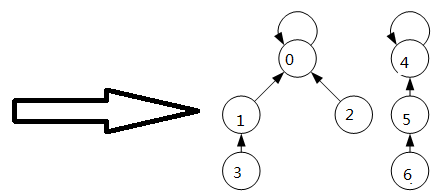
可以通过hash来简化这个过程，元素按照1234567 来区分，对应数组0123456下标，存储的内容就是父节点，表达的意思是和其父节点是亲戚关系。

初始化，数组初始存储值是其本身，表示没有关系

初始数组0123456，其中456为第二个集合

输入ab，数组变为0023456，1的父节点是0表示他们是亲戚关系

输入bd，数组变为0021456，3的父节点是1他们是亲戚关系

输入ac，数组变为0001456,2的父节点是0

第一组集合输入完毕，对于第二组集合

输入ef，数组变为0001446

输入fg，数组变为0001445

上述输入是关于数组的合并操作，对应代码