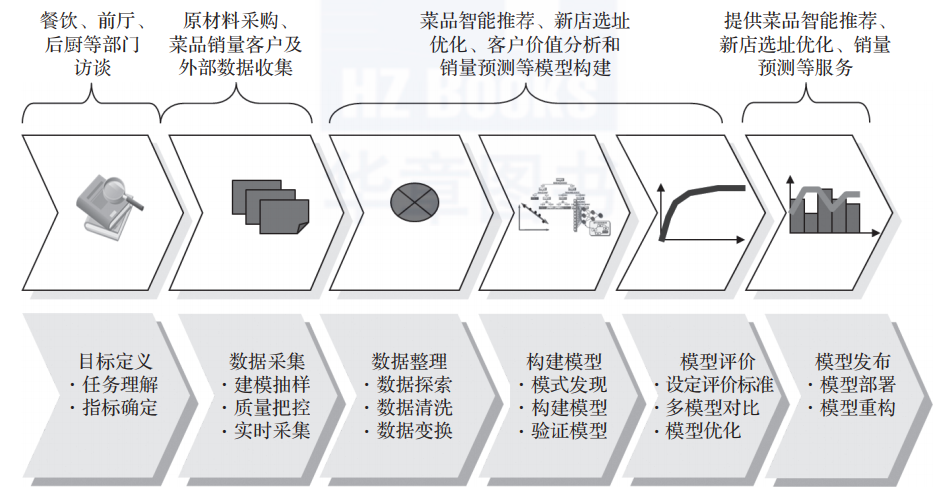
想要了解聚类算法并对其进行区别与比较的话，最好能把聚类的具体算法放到整个聚类分析的语境中理解。

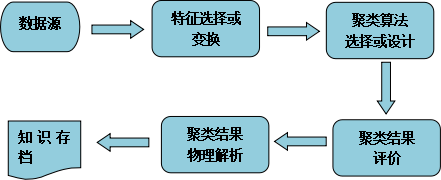
聚类分析是一个较为严密的数据分析过程。从聚类对象数据源开始到得到聚类结果的知识存档，共有四个主要研究内容

聚类分析过程：

1984年，Aldenderfer等人提出了聚类分析的四大功能: 一是数据分类的进一步扩展; 二是对实体归类的概念性探索; 三是通过数据探索而生成假说; 四是一种基于实际数据集归类假说的测试方式。

在很多情况下，样本数据集并没有分类，即每一个数据样本都没有分类标签。一般而言，聚类指将没有分类标签的数据集，分为若干个簇的过程，是一种无监督的分类方法。实际上，很难对聚类下一个明确的定义。

2001 年，Everitt 等人甚至指出提出聚类的正式定义不仅困难而且也没有必要，因为聚类分析本身是一种建立在主观判断基础上的相对行之有效的方法。Hansen 也已经作了数学上的阐述，给定一个数据样本集:

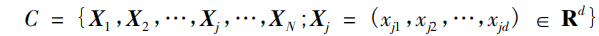
这里，Xj表示一个向量，称为样本点或者样本; Xjd表示一个变量，通常称为属性、特征、变量或维等。

划分聚类将数据集分为 K 个簇，需满足:

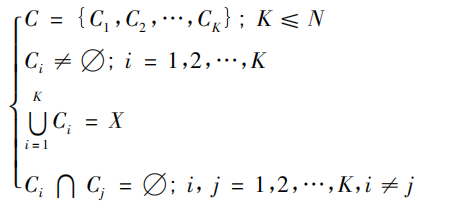
而层次聚类是将数据集构建成一种树状的结构，即:

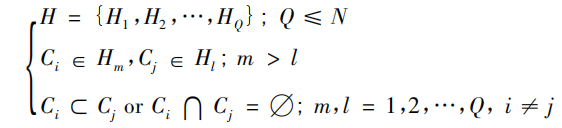
由于聚类分析属于一个交叉研究领域，融合了多个学科的方法和技术，故可以从多种角度、多个层次来分析现有的聚类分析算法。

Agarwal 关于数据聚类的经典长文从统计模式识别的视角总结了 1999 年之前的经典模式聚类方法；Qian Zhou从聚类标准、聚类表示及算法框架角度分析了多个流行的聚类算法；Grabmeier 和 Rudolph从数据挖掘的角度(如相似度和距离度量的严格区分、应用到聚类中的相 关优化标准等)分析了一些聚类方法，还讨论了 IBM 公司的智能挖掘器(Intelligent Miner)中聚类算法的使用演示等等。

传统的聚类算法大致可以分为划分聚类方法、层次聚类方法、密度聚类方法、网格聚类方法、模型聚类方法等。近年来，量子聚类方法、谱聚类方法、粒度聚类方法、概率图聚类方法、同步聚类方法等也流行起来。

聚类算法的研究已经开展了几十年，迄今为止，已公开发表了近千种聚类算法，但没有一种聚类算法敢声称是通用的、普适的。

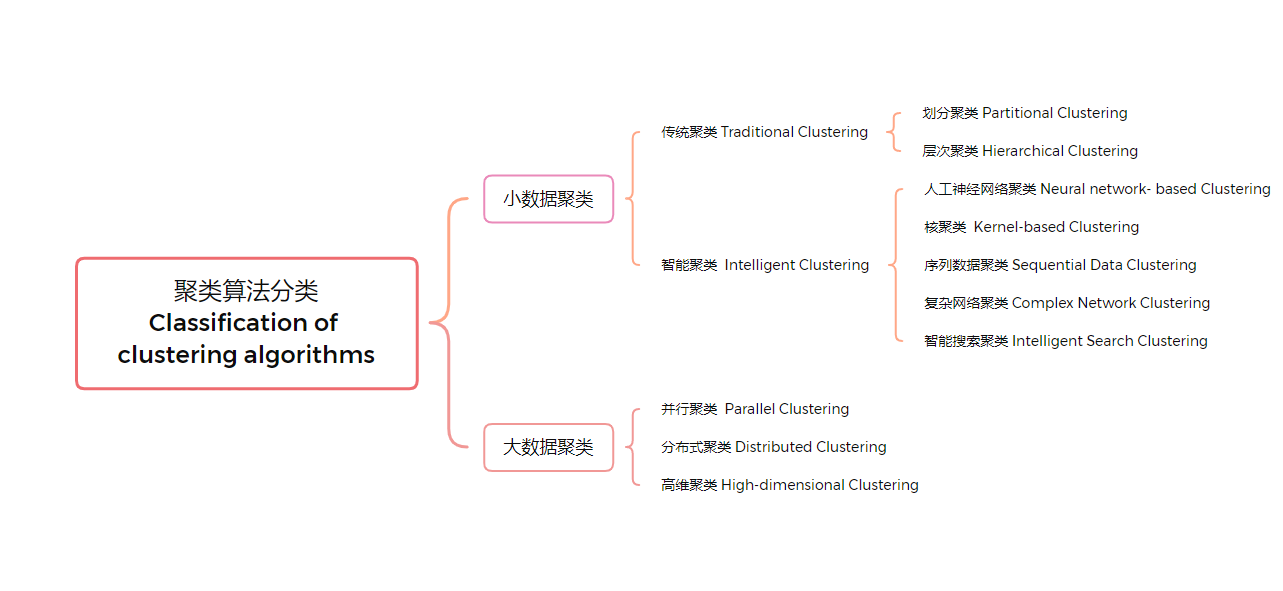
聚类算法的分类

聚类算法一般可以用基于划分、基于层次、基于密度、基于网格、基于模型、基于图等方式来进行分类。

基于划分的聚类算法

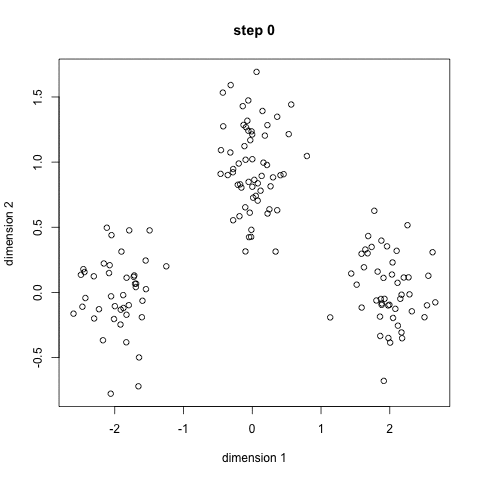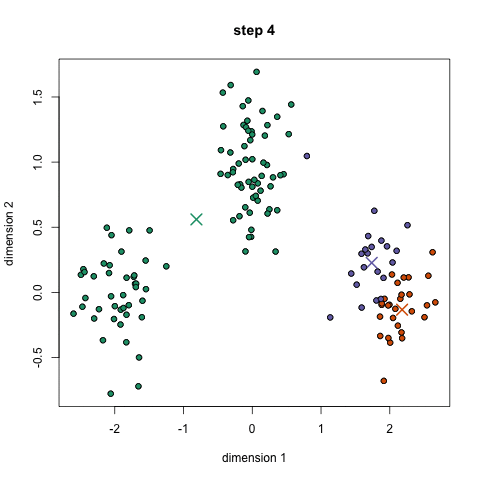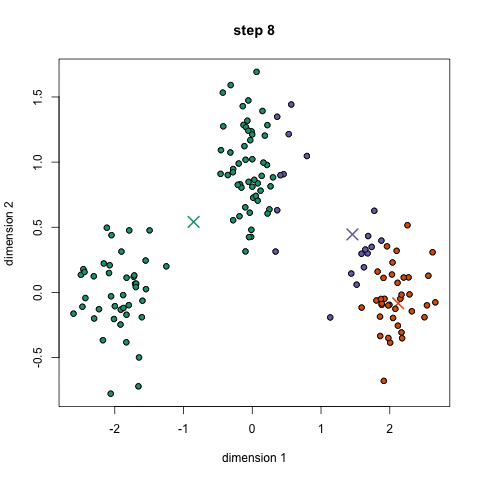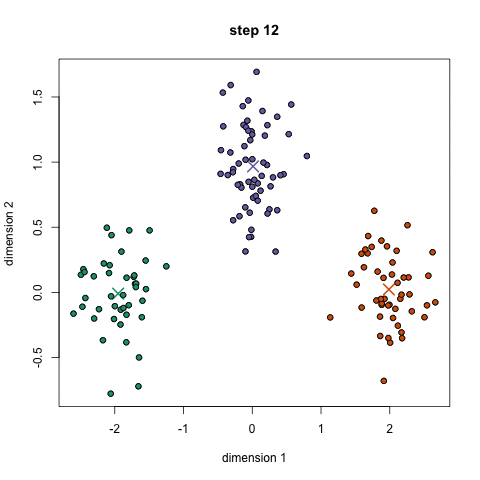
基于划分的聚类算法通过构造一个迭代过程 来优化目标函数，当优化到目标函数的最小值或极小值时，可以得到数据集的一些不相交的子集，通常认为此时得到的每个子集就是一个聚类。多数基于划分的聚类算法都是非常高效的，但需要事先给定一个在聚类分析前难以确定下来的聚类数目。k-means算法和 FCM(Fuzzy C Means)算法是该类型中最著名的两个算法。

基于层次聚类算法

层次聚类方法使用一个距离矩阵作为输入，经过聚类后得到一个反映该数据集分布状况的聚类层次结构图，其时间复杂度至少为 T＝O(n2logn)。

层次聚类算法通常分为两种：

第一种是凝聚的层次聚类算法，它首先把每个数据点看作是一个聚类，然后以一种自底向上的方式通过不断地选择最近邻居聚类对的合并操作，最终可以构造出一 棵代表着该数据集聚类结构的层次树。

第二种是分裂的层次聚类算法，它首先把所有的数据点看作是一个聚类，然后以一种以自顶向下的方式通 过不断地选择最松散簇进行分裂操作，最终可以 构造出一棵代表着该数据集聚类结构的层次树。

基于密度的聚类算法

基于划分的聚类算法通常更适合于发现凸形聚类簇，但对于任意形状的聚类簇，它就显得有些力不从心了。基于密度的聚类算法试图通过稀疏区域来划分高密度区域以发现明显的聚类和孤立点，主要用于空间型数据的聚类。 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)算法就是一个最为著名的基于密度的聚类算法。

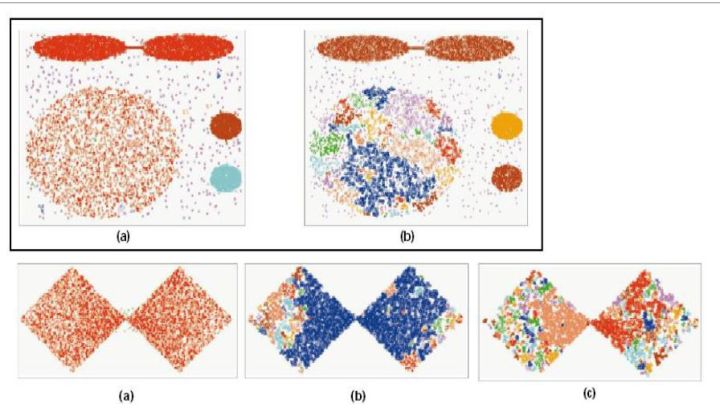
DBSCAN对参数设置的敏感表现

基于网格的聚类算法

基于网格的聚类算法是一种基于网格的具有多分辨率的聚类方法。它首先将数据集的分布空 间划分为若干个规则网格(如超矩形单元)或灵活 的网格(如任意形状的多面体)，然后通过融合相 连的带数据概要信息的网格来获得明显的聚类。显然，几乎所有的基于网格的聚类算法都属于近似算法，它们能处理海量数据。这类算法的优点是处理时间与数据点的数目无关、与数据的输入顺序无关，可以处理任意类型的数据。其缺点是处理时间与每个维度上所划分的单元数相关，一定程度上降低了聚类的质量和准确性。STING(STatistical INformation Grid)算法和CLIQUE(CLustering In QUEst)是基于网格的聚类算法的典型代表。

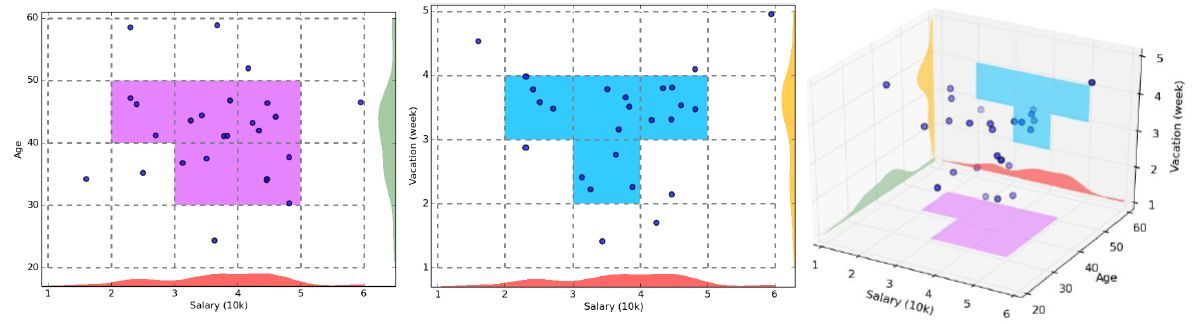
基于模型的聚类算法

基于模型的聚类算法借助于一些统计模型来获得数据集的聚类分布信息。该方法假定数据集是由有限个概率分布模型共同作用生成的。在这种方法中，多变量的高斯分布混合模型应用最为广泛。其中，Fish提出的 COBWEB、 Gennarim 提出的 CLASSI、 Cheeseman 和 Stutz提出的 AutoClass 是较为有名的几个模型聚类方法。

在实际应用中，有时使用基于模型的聚类算法或其他聚类算法来获取数据集的聚类中心点集，然后再用学习向量化方法来构造分类器。

基于图的聚类算法

采用图聚类方法进行聚类分析时，首先是建立与具体问题相适应的图。图的结点代表被分析数据的基层单元，图的边代表基层单元数据之间的相似性度量(或相异性度量)。通常，每个基层单元数据之间都会有一个度量表达，这样可以保持数据集的局部分布特性。图聚类方法是以数据集的局部连接特征作为聚类的主要信息源，因而易于处理局部数据的特性。Karypis 提出的变色龙算法也可看作是一种图聚类算法。

小数据聚类和大数据聚类

然而，在大数据时代背景下，随着数据量的不断增加及其数据形态的日益多样化，聚类算法的应用更加广泛; 同时对算法本身也提出了更高的要求。ZHANG Yonglai，ZHOU Yaojian依据有效数据量10字节为阈值，将聚类算法分为小数据聚类和大数据聚类两大类。小数据聚类主要体现的是聚类的基本思想，而大数据聚类的思想主要体现在理念、体系结构与架构等几个方面，至于底层聚类的具体实现算法，其实与小数据聚类算法并没有本质上的差别。换言之，大数据聚类的具体实施算法依然采用小数据聚类技术。

21世纪是一个信息化、数据化和知识化的时代，信息技术正改变着人类社会的方方面面。随着数据挖掘的兴起，聚类方法开始用于分析实际问题中经常出现的具有多种类型属性和复杂分布结构的数据集。现如今，聚类研究及其应用领域非常广泛，已经应用到多个领域，如机器学习、模式识别、图像处理、信息检索、IP地址定位等。

聚类算法是伴随着统计学、计算机学与人工智能等领域的发展而逐步发展起来的科学，因此，当这些领域有比较快速的发展进程时，势必会促进聚类算法的快速发展与应用。比如机器学习领域的人工神经网络与支持向量机的发展就促生了基于神经网络的聚类方法与核聚类方法。目前，基于人工神经网络的深度学习( 如与职业九段棋手李世石、世界排名第一的世界围棋冠军柯洁对战的AlphaGo ) 也必将推动聚类分析方法的进一步发展。