目录
1 正弦波
1.1 调整顶点
1.2 调整Y
1.3 振幅
1.4 波长
1.5 速度
1.6 法线向量
1.7 Mesh分辨率
1.8 阴影
2 格斯特纳波（Gerstner）
2.1 来回移动
2.2 法线向量
2.3 防止循环
2.4 相速度
3 波方向
3.1 方向向量
3.2 法线向量
4 多重波
4.1 单参数向量
4.2 两个波
4.3 循环动画
4.4 循环波
4.5 三个波
收起
本文重点：
1、顶点动画
2、创建格斯特纳波浪（Gerstner ）
3、控制波浪方向
4、合并多波浪
这是有关流体材质的第三篇教程。前两篇的内容都是如何处理纹理动画，这个章节我们讲如何通过顶点位置动画来产生波浪。
本教程是CatLikeCoding系列的一部分，原文地址见文章底部。“原创”标识意为原创翻译而非原创教程。
教程使用Unity2017.4.4f1创建。
（让我们一起来浪吧）
1 正弦波
设置纹理动画可以创建运动表面的错觉，但网格表面本身保持静止。这对于较小的波纹很好，但不能代表较大的波浪。在大片水域（如大湖海洋）上，风会产生大波浪，并能持续很长时间。为了表示这些风浪，我们将使用正弦波函数制作新的着色器，在垂直方向移动网格顶点。
1.1 调整顶点
创建一个名为Waves的新表面着色器。让片段表面功能保持不变。添加另一个函数vert来调整顶点数据。此函数具有单个顶点参数，用于输入和输出。我们将使用Unity的默认顶点数据结构appdata_full。
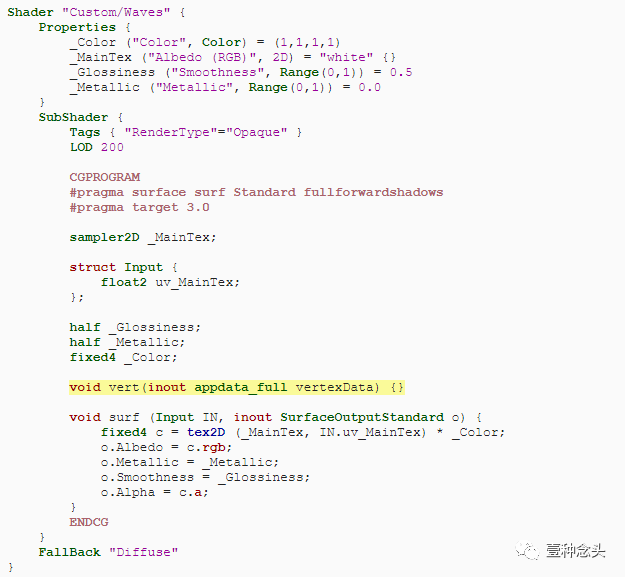
若要指示表面着色器应使用vertex函数，请将vertex：vert添加到surface pragma指令。
创建一个使用此着色器的新Waves材质。我给它提供了与其他两种材质相同的albedo和smoothness。
（Wave材质）
因为我们要置换顶点，所以这次不能使用四边形。而是通过GameObject 3D Object Plane创建一个默认平面，并使用Waves材质。这使我们可以使用10×10的四边形网格。
（Waves 平面, wireframe视角下）
1.2 调整Y
忽略Z维度，将每个顶点的位置定义为 P = [x，y]，其中P是其最终位置，x是原始X坐标，而y是原始Y坐标，两者 都是在对象空间中。要创建波，我们必须调整P 的Y分量。生成波的最简单方法是使用基于x 的正弦波，因此 y = sinx。那么最后，该点是P = [x，sinx]。
（单个波）
结果是沿X方向的正弦波，沿Z方向恒定。平面的四边形具有单位大小，因此整个平面覆盖以其本地原点为中心的10×10区域。因此，我们最终看到正弦波的10/2π≈1.59周期。
1.3 振幅
正弦波的默认振幅为1，但我们不能局限于此。向着色器添加一个属性，以便我们可以使用 Py = asinx代替，其中a是振幅。
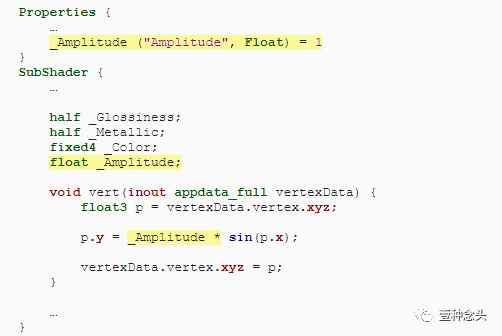
（振幅设置为2）
1.4 波长
这个例子中是sinx，正弦波的总长度为 2 π ≈ 6.28 2π≈6.28。这是波长，我们也可以对其进行配置。
为了轻松控制波长，我们首先用2π乘以X然后除以所需的波长。所以我们最后得到 （ 2 π X /λ ） sin（2πx/λ），其中 λ （λ）是波长。
2π除以λ被称为波数k =2π/λ。我们可以将其用作shader属性，因此不需要在shader中执行除法。这是一个有用的优化，但是在本教程中，我们将坚持使用对开发者更加友好的波长。
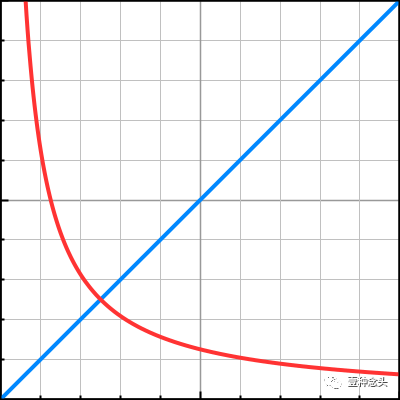
（λ （从0到10线性）和 k）
在着色器中，我们将显式使用波数，因此最终得到 Py = asin（kx）。
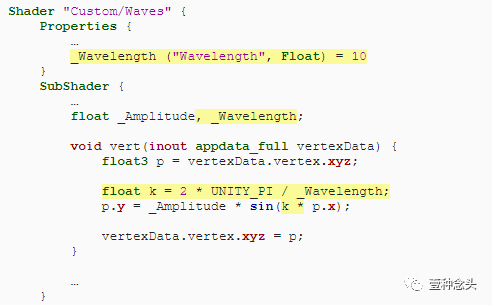
（波长为10 振幅为1）
1.5 速度
波浪需要移动，因此我们必须定义速度。使用相位速度c最为方便，该速度定义了整个波以每秒单位的速度移动。这是通过使用时间偏移量kct来完成的。为了使波向正方向移动，我们必须从kx中减去它，因此我们得出Py = sin（kx-kct ）= sin（k（x-ct））。
（速度设置为5）
1.6 法线向量
我们的曲面是弯曲且移动的，但灯光仍然是静止的平面。那是因为我们还没有改变顶点法线。让我们直接查看X维度T上的表面切向量，而不是直接计算法线向量。对于平坦表面 T = [x'，0] = [1，0 ]，它对应于原始平面的切线。但是对于我们的波，我们必须使用T = P'= [x'，asin（k（x-ct））']。
正弦的导数是余弦，所以 sin'x = cosx。但是在我们的例子中，正弦的论点本身就是一个函数。我们可以说我们有 Py = asinf，其中 f = k（x-ct）。
我们必须使用链式规则，（Py）'= f'acosf。f'= k，因此我们得出T = [1，kacosf]。这是有道理的，因为更改波长也会更改波的斜率。为了在着色器中获得最终的切向量，我们必须归一化T。
法线向量是两个切向量的叉积。由于我们的波在Z维度上是恒定的，因此双法线始终是单位矢量并且可以忽略，因此我们得到 N = [-kacosf，1]。我们只需要在对它们进行归一化之后就可以获取它们。
（正确的法向量）
1.7 Mesh分辨率
当使用10波长时，我们的波看起来不错，但对于小波长而言，效果却不佳。例如，波长为2时会产生锯齿波。
（波长为2 速度为1）
波长为1根本不产生波，而是整个平面均匀地上下波动。其他小的波长会产生更加丑陋的波，甚至可以向后移动。
此问题是由我们的平面网格的有限分辨率引起的。由于顶点之间相隔一个单位，因此无法处理2个或更小的波长。通常，必须保持波长大于网格中三角形边缘长度的两倍。你不想将他们剪得太近，因为由两个或三个四边形组成的波浪看起来并不好。
可以使用更大的波长，也可以提高网格的分辨率。最简单的方法是只使用另一个网格。这是一个替代平面网格，由100×100个四边形组成，而不仅仅是10×10。每个四边形仍为1×1单位，因此您必须缩小波形属性并将其乘以10才能获得与以前相同的结果。
（大的平面 波的设置全部x10，并且放大）
1.8 阴影
尽管我们的表面看起来不错，但尚未与阴影正确交互。它仍然像平面一样，可以投射和接收阴影。
（不正常的阴影）
解决方案是将addshadow包括在Surface编译指示中。这指示Unity为我们的着色器创建一个单独的阴影投射器通道，该通道也使用我们的顶点位移功能。
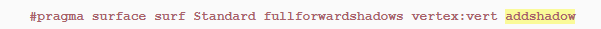
阴影现在是正确的，波浪也可以正确地自阴影化。由于我们现在正在大的缩放下工作，因此可能必须先增加阴影距离，然后阴影才会出现。
（正确的阴影，阴影距离为300）
在本教程的其余部分中，我会禁用阴影。
2 格斯特纳波（Gerstner）
正弦波很简单，但它们与实际水波的形状不匹配。大风引发的波浪实际上是由斯托克斯（Stokes ）波函数建模的，但它相当复杂。相反，Gernster波通常用于水面的实时动画。
Gerstner波以发现它们的Franti?ek Josef Gerstner的名字命名。它们也被称为摆线波，以其形状命名，或周期性的表面重力波，描述其物理性质。
2.1 来回移动
当波浪在水表面上移动时，基本的观察结果是，水本身并不会随之移动。在正弦波的情况下，每个表面点都会上下移动，但不会水平移动。
但是实际的水不仅仅只有表面。下面还有更多的水。当表面的水向下移动时，其下方的水会怎么运动？当表面向上移动时，什么填充了其下面的空间？事实证明，表面点不仅向上和向下移动，而且也向前和向后移动。它们有一半的时间与波一起移动，而另一半则沿相反的方向移动。表面以下的水也是如此，但越深，运动就越少。
具体来说，每个表面点都绕一个固定的锚点绕圆周运动。随着波峰的接近，该点向其移动。波峰经过后，它会向后滑动，然后出现下一个波峰。结果是水在波峰中聚拢，并在波谷中散布开来，我们的顶点也会发生同样的情况。
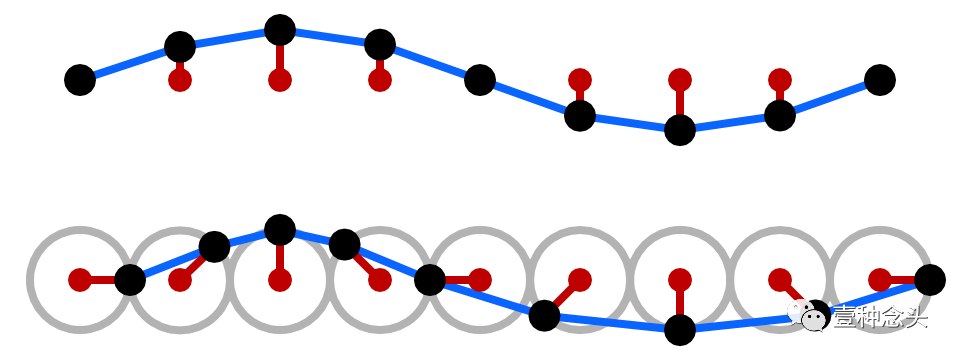
（正弦波与格斯特纳波）
实际上，表面点确实会漂移并且不是完美的圆，但是Gerstner Wave并不是对此进行建模的。我们把原始顶点位置用作锚点。
我们可以通过使用P = [acosf，asinf]将正弦波变成一个圆，但这会将整个平面折叠成一个圆。相反，我们必须将每个点锚定在其原始X坐标上，因此我们需要 P = [x + acosf，asinf]。
（Gerstner波，振幅10，波长100，速度50）
结果是，与常规正弦波相比，其波峰和波谷更平坦
Gersner Wave不是应该该用SinX和 cosY？
这是定义它们的常规方法，但是正如我们已经使用sin Y，那么X就直接用Cos了。其他方法相比唯一的不同是，波的周期偏移了四分之一。
2.2 法线向量
由于我们更改了表面函数，因此其导数也发生了变化。T的X分量曾经是x'= 1，但现在有点复杂了。余弦的导数为负正弦，因此我们得出T = [1-kasinf，kacosf]。
（正确的法线向量）
2.3 防止循环
尽管产生的波浪看起来不错，但并非总是如此。例如，将波长减小到20却将幅度保持在10会产生奇怪的结果。
（波循环，波长20）
因为振幅相对于波长而言非常大，所以表面点过调并在表面上方形成回路。如果这是真实的水，那么海浪会破裂并散开，所以我们无法用格斯特纳海浪来表示。
通过观察当 ka大于1时Tx可以变为负数，我们可以从数学上看到为什么发生这种情况。这种情况下，切向量最终指向后方而不是向前。当 ka为1时，我们得到的切线向量指向正上方。
实际上，在波峰两侧之间的角度超过120°的情况下，我们就不会得到完整的波浪了。Gerstner波没有这个限制，但是我们不想低于0°，因为那样就会产生表面循环。
波长和波幅之间存在关系。我们可以使用 a = ekb/k，其中b与表面压力有关。压力越大，波浪越平坦。在零压力的情况下，我们最终得到a = 1k，这将产生0°的波峰，这是循环之前最尖的。我们可以改用a = s/k，其中s是陡度的度量，介于0和1之间，更易于使用。那么我们有P = [x + s/k cosf，s/k sinf]，这简化了我们与T = [1-ssinf，scosf]的切线。
（陡度替代振幅。）
2.4 相速度
实际上，波没有任意相位速度。它与波数有关
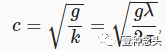其中g是引力，在地球上约为9.8。深水中的波浪确实如此。在浅水中，水深也起着一定的作用，但我们在这里不做介绍。尽管我们可以使用正确的材质属性，但在着色器中进行计算更加方便。
现在我们可以消除速度属性。
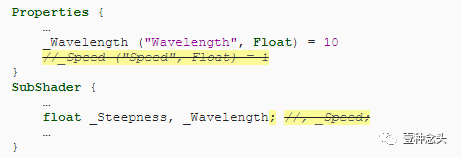
注意，这种关系意味着更长的波具有更高的相速度。同样，重力越强，运动速度就越快。
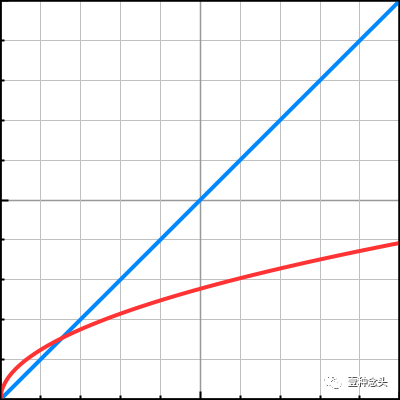
（λ（线性，从0到100）和 C）
3 波方向
到目前为止，我们的波只在X维度上移动。现在，我们将删除此限制。这使得我们的计算更加复杂，因为构造最终波及其切向量需要同时使用X和Z。
3.1 方向向量
为了指示波的传播方向，我们将引入方向矢量 D = [Dx，Dz]。这纯粹是方向的指示，所以它是单位长度的向量， || D || = 1。
现在，x 对波函数的贡献由D 的X分量调制。因此我们得到f = k（DxX-ct）。但是z 现在也以相同的方式发挥作用，导致f =f = k（DxX + DzZ-ct）。换句话说，我们使用DD与原始X和Z坐标的点积。因此，我们最终得到f = k（D?[x,z] -ct）。
将方向属性添加到我们的着色器，并将其合并到我们的函数中。它应该是一个单位长度的向量，但是为了使其更易于使用，我们将在着色器中对其进行标准化。请注意，所有矢量属性均为4D，因此只需忽略Z和W分量。
我们还必须调整Px和 Pz的水平偏移，以使其与波方向对齐。因此，不仅要将偏移量添加到x 上，我们还必须将偏移量也添加到z 上，在两种情况下都由D 的适当分量进行调制。因此最终的计算成为
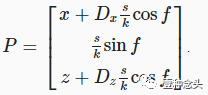
（方向设置为 [0,1] 和[1,1]）
3.2 法线向量
再一次，我们必须调整切线的计算，而不仅仅是调整X尺寸。现在，我们还必须计算Z维上的切线，即双法线向B．
X方向上f 的偏导数为fx'= kDx。在Tx和Ty的情况下，这仅意味着我们将Dx再乘一次。除此之外，我们还必须加上Tz，因为它不再为零。最终切线为：
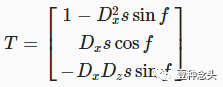
双重法线相同，除了 fz'= kDz，我们乘以Dz，以及X和Z组件的角色互换。所以B=
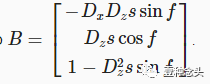
现在我们确实需要采取适当的叉积来找到法线向量。
（正确的法线向量）
注意 Tz ＝ Bx。我们不需要为此进行优化，因为着色器编译器会处理此问题，就像正弦和余弦仅计算一次一样。
4 多重波
实际上，很少会发现只有一个均匀的波在水面上传播。取而代之的是，有许多波以大致相同的方向传播。我们也可以通过累积多个波来改善效果的真实感。
合并多个波只是添加所有偏移即可。数学上，对于P的X分量，我们得到
这是和以前相同的公式，只是增加了总和。P 的其他分量和切线也是如此。
4.1 单参数向量
每个单独的波都有其自己的属性。为了使此操作更易于管理，让我们将wave的所有属性合并到一个着色器属性中。我们可以将它们拟合为单个4D向量，其中X和Y表示方向，Z表示陡度，W表示波长。使用此技巧为我们的第一个浪潮A浪定义一个属性。
（波A的设置）
用新的波矢替换旧变量。
然后将波动代码移至新的GerstnerWave函数。此功能将波浪设置作为参数，后跟原始网格点。同时给它输入切线和双法线的输入输出参数，这样我们就可以对其进行累加。它返回其点偏移量。
因为它会累积偏移量，所以请保留 X 和 Z部分超出结果。因此，也应从导数中省略它们，并消除1。最后，不会对每个单独的波进行归一化。
波浪现在相对于平面。因此，我们从原始网格点以及默认的切线和双法线向量开始，然后调用GerstnerWave并将其结果添加到最终点。之后，通过叉积和归一化创建法线向量。
4.2 两个波
要添加对第二个wave的支持，我们要做的就是添加另一个wave属性并再次调用GerstnerWave。我没有在浪B的标签上重复数据描述，因为它与浪A相同。
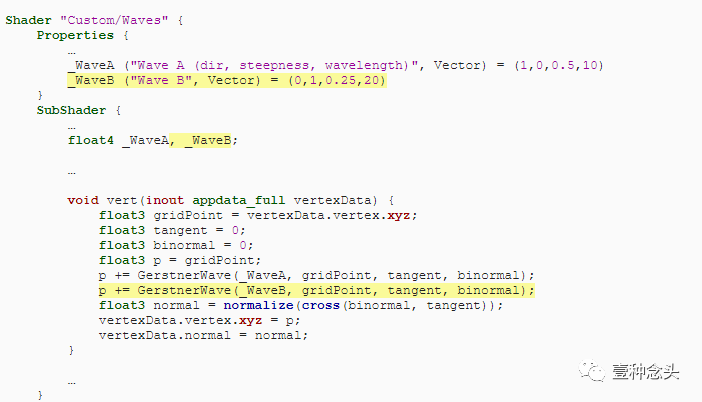
（两个波浪）
4.3 循环动画
现在我们有了两个波，你可以观察到波长较长的波的确比短波长的波快。但是相速度和波长之间的关系是非线性的，因为
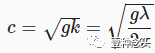
当你要创建具有多个波形的循环动画时，他们是相关的。对于两个波，你必须找到两个波长，它们产生的相速度为 ac1 = bc2，其中a和b 是整数。你可以通过对波长使用2的偶次幂来做到这一点。
比如，
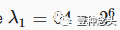
并且
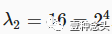
那么
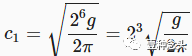
观察到
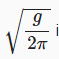
是常数，因此我们可以将其定义为q，并使用
和
。因此 c1 = 2c2，这意味着每次大波重复一次，小波重复两次。循环持续时间等于大波的周期，即
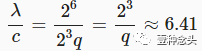
秒。
（方向 [1，0]，陡度?，波长64和16）
你也可以重写数学，以便直接控制相速度并从中得出波长。
4.4 循环波
另一个重要的观察结果是，我们可以再次得到循环波。如果偏导数之和超过1，则会形成循环。为了防止产生波动，你必须确保所有波动的陡度总和不超过1。
（具有两个波的循环 陡度为1）
你可以通过规范化着色器的steepness 来实施此限制。这意味着，如果更改一个波的陡度，它将影响所有其他波。或者，你可以将所有陡度值除以波浪数，但这会限制每个波浪的陡度。你也可以在着色器中不设置任何限制，而是通过材质检查器提供反馈和选项。对于本教程，我们没有设置任何限制。
4.5 三个波
最后，我们增加了对另一波的支持。添加的波越多，我们的着色器就越复杂。你可以根据波的数量进行着色器变化，但我们将固定数量设为三个。
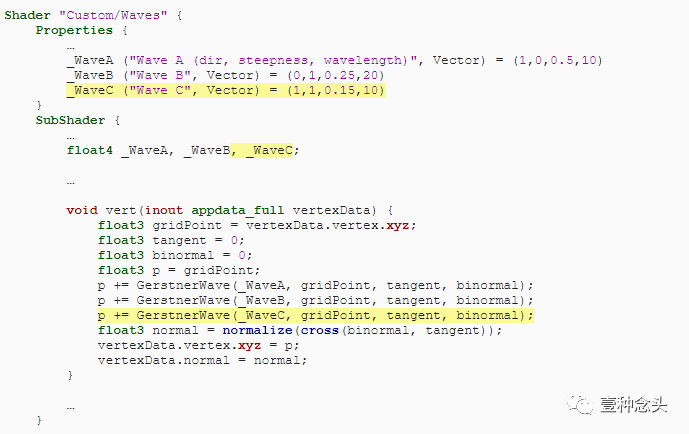
（三个波）
欢迎扫描二维码，查看更多精彩内容。点击 阅读原文 可以跳转原教程。
本文翻译自 Jasper Flick的系列教程
原文地址：
https://catlikecoding.com/unity/tutorials
本文分享自微信公众号 - 壹种念头（OneDay1Idea）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。
