应用场景

1. 图像识别与检索
2. 人脸识别
3. 性别/年龄/情绪识别
4. 物体检测
5. 视频处理
6. 语音分析

概述

一般一个卷积神经网络由多个卷积层构成，在卷基层内部通常会有如下几个操作：

1. 图像通过多个卷积核滤波，添加偏置，提取局部特征每个卷积核会映射出一个新的2D图像。
2. 卷积核的滤波结果输出到激活函数中，激活函数通常选ReLU
3. 对激活函数的结果进行池化操作，池化就是对图像分割成不同的小区域后取平均值或最大值。一般取最大值。

上述几个步骤就构成了最常见的卷积层。在池化的后面还可以加上batch normalization等操作。

一个卷积层中可以有不同的卷积核，而每一个卷积核都对应一个滤波后映射出的新图像，同一个新图像的每一个像素都来自完全相同的卷积核。这种卷积核的权值共享可以有效降低模型负责度，减轻过拟合，减少计算量。

卷积神经网络结构

建立卷积神经网络对手写数字识别问题进行优化，构建由两个卷积层（包含池化层），两个全连接层构成的卷积神经网络。输入图像是28×28的单通道数据，输出是10×1的one_hot编码的向量。

第一层：卷积核大小是[5,5]，输入通道1，输出通道32，padding选择SAME模式，激活函数为relu。
第二层：池化层，池化核大小是[2,2]，步长[2,2]。
第三层：卷积核大小是[5,5]，输入通道32，输出通道64，padding选择SAME模式，激活函数为relu。
第四层：池化层，设置同上。
第五层：全连接层，首先将图像数据矩阵flatten化，变成1维向量，输出维度是1024， 之后dropout掉一定的数据防止过拟合
第六层：全连接层，输出维度10，激活函数为softmax

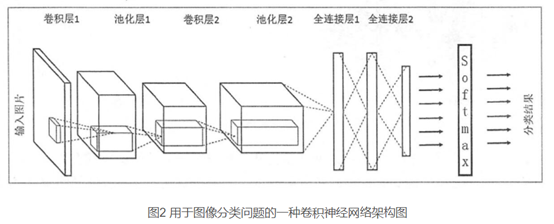
一个卷积神经网络主要由以下五种结构组成：
（1）输入层 输入层是整个神经网络的输入，在处理图像的卷积神经网络中，它一般代表了一张图片的像素矩阵。从输入层开始，卷积神经网络通过不同的神经网络结构将上一层的三维矩阵转化为下一层的三维矩阵，直到最后的全连接层。
（2）卷积层 前一层的特征图与卷积核进行卷积运算，运算的结果再加偏置，经过激活函数后形成这一层的神经元，每个神经元的输入与前一层局部感知野 (receptive field)相连接，并提取该局部特征。一单该局部特征被提取，它与其他特征之间的位置关系就被确定。卷积层中每一个节点的输入只是上一层神经网络的一小块，这个小块(也叫过滤器，滤波器，卷积核，权重)常用的大小有3×3或5×5。卷积层试图将神经网络中的每一小块进行更加深入地分析从而得到抽象程度更高的特征。一般通过卷积层处理过的节点矩阵会变得更深。

卷积神经网络有两种神器可以降低参数数目。
　　第一种神器叫做局部感知野，一般认为人对外界的认知是从局部到全局的，而图像的空间联系也是局部的像素联系较为紧密，而距离较远的像素相关性则较弱。因而，每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部的信息综合起来就得到了全局的信息。
　　第二种神器，即权值(权重或卷积核或过滤器)共享。

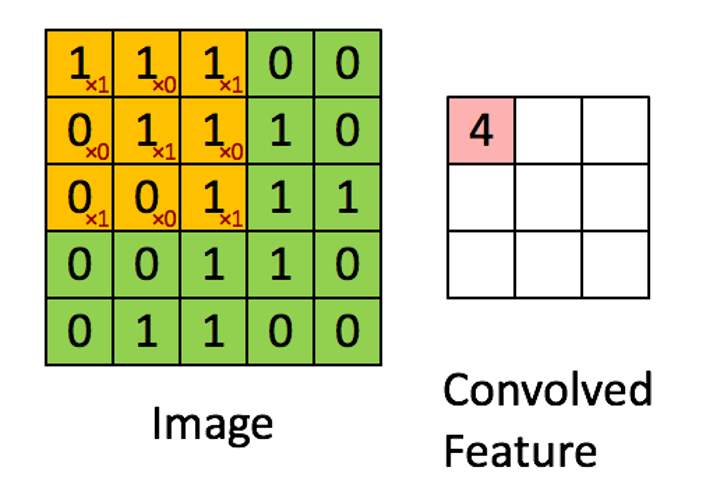
上述操作处理图像得到新图像的操作称为卷积, 在图像处理中卷积核也被称为过滤器(filter).

卷积得到的结果矩阵通常用于表示原图的某种特征(如边缘), 因此卷积结果被称为特征图(Feature Map).

每个卷积核可以包含一个偏置参数b, 即对卷积结果的每一个元素都加b作为输出的特征图.

（3）池化层
池化层神经网络不会改变三维矩阵的深度，但可以缩小矩阵的大小。池化操作可以认为是将一张分辨率较高的图片转化为分辨率较低的图片。通过池化层，能进一步缩小最后全连接层中的节点数，达到减少整个神经网络中参数的目的。这层利用图像局部相关性的原理，对图像进行子抽样，可以减少数据处理量同时保留有用信息，相当于图像压缩。

用16个小方阵的均值组成一个4x4方阵便是均值池化, 类似地还有最大值池化等操作. 均值池化对保留背景等特征较好, 最大值池化对纹理提取更好. 随机池化则是根据像素点数值大小赋予概率(权值), 然后按其加权求和.

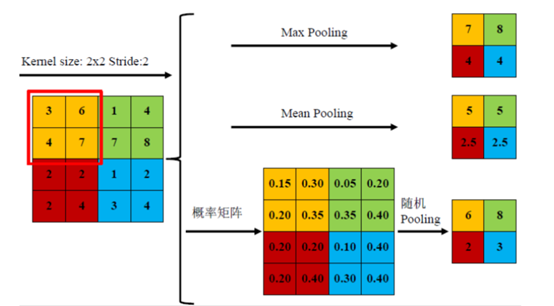
池化操作用于减少图的宽度和高度, 但不能减少通道数。

（4）全连接层
输入信号经过多次卷积池化运算后，输出为多组信号，经过全连接运算，将多组信号一次组合为一组信号。可以将卷积层和池化层看成自动图像特征提取的过程。在特征提取完成后，需要使用全连接层来完成分类任务。

（5）Softmax层
用于分类问题，得到当前样例属于不同种类的概率分布情况。

卷积操作细节，输入输出维度的思维训练

"""
卷积神经网络 解决全连接神经网络参数过多的问题。
tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)
input： 需要做卷积的图像，是一个tensor，形状是 [batch, in_height, in_width, in_channels].具体含义是：
      “训练一个batch的图片数量，图片高度，图片宽度，图片通道数”，注意这是一个四维的tensor。要求类型为float32或float64.
filter: 相当于CNN的卷结核，是一个tensor，具有[filter_height, filter_width, in_channels, out_channels]具体含义是：
        "卷积核的高度，滤波器的宽度，图像通道数，滤波器个数"，要求类型与input相同。有一个地方需要注意，第三维in_channels,就是
        input的第四维。
strides: 卷积时在图像每一维的步长，这是一个一维的向量，长度 4
padding: 定义元素边框与元素内容之间的空间。值为“VALID”表示边缘不填充，“SAME”表示填充到滤波器可以到达图像边缘。
use_cudnn_on_gpu： bool类型，是否使用cudnn加速，默认使用。
返回值：是一个tensor,即 feature map.

"""
import tensorflow as tf

# [batch, in_height, in_width, in_channels] [训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]
# 定义三个输入变量，来模拟输入图片。分别是 5x5大小 1个通道的矩阵。。。并将里面的的值统统赋值为1
input = tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 1]))
input2 = tf.Variable(tf.constant(1.0, shape=[1, 5, 5, 2]))
input3 = tf.Variable(tf.constant(1.0, shape=[1, 4, 4, 1]))

# [filter_height, filter_width, in_channels, out_channels] [卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]
# 定义5个卷积核变量, 每个卷积核都是2x2的矩阵, 只是输入，输出的通道数有差别.
filter1 = tf.Variable(tf.constant([-1.0, 0, 0, -1], shape=[2, 2, 1, 1]))
filter2 =  tf.Variable(tf.constant([-1.0,0,0,-1,-1.0,0,0,-1],shape = [2, 2, 1, 2]))
filter3 =  tf.Variable(tf.constant([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1],shape = [2, 2, 1, 3])) # 输入1通道，输出3通道。
filter4 =  tf.Variable(tf.constant([-1.0,0,0,-1,
                                    -1.0,0,0,-1,
                                    -1.0,0,0,-1,
                                    -1.0,0,0,-1],shape = [2, 2, 2, 2]))
filter5 =  tf.Variable(tf.constant([-1.0,0,0,-1,-1.0,0,0,-1],shape = [2, 2, 2, 1]))

# 定义卷积操作
# padding的值为‘VALID’，表示边缘不填充, 当其为‘SAME’时，表示填充到卷积核可以到达图像边缘
op1 = tf.nn.conv2d(input, filter1, strides=[1, 2, 2, 1], padding='SAME')  # 1个通道输入，生成1个feature map， 步长为2x2
op2 = tf.nn.conv2d(input, filter2, strides=[1, 2, 2, 1], padding='SAME')  # 1个通道输入，生成2个feature map， 步长为2x2
op3 = tf.nn.conv2d(input, filter3, strides=[1, 2, 2, 1], padding='SAME')  # 1个通道输入，生成3个feature map， 步长为2x2

op4 = tf.nn.conv2d(input2, filter4, strides=[1, 2, 2, 1], padding='SAME') # 2个通道输入，生成2个feature
op5 = tf.nn.conv2d(input2, filter5, strides=[1, 2, 2, 1], padding='SAME') # 2个通道输入，生成一个feature map

vop1 = tf.nn.conv2d(input, filter1, strides=[1, 2, 2, 1], padding='VALID') # 5*5 对于pading不同而不同
op6 = tf.nn.conv2d(input3, filter1, strides=[1, 2, 2, 1], padding='SAME')
vop6 = tf.nn.conv2d(input3, filter1, strides=[1, 2, 2, 1], padding='VALID')  #4*4与pading无关

init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    # print("op1:\n",sess.run([op1, filter1]))# 1-1  后面补0
    # print("------------------")
    #
    print("op2:\n",sess.run([op2,filter2])) #1-2多卷积核 按列取
    print("op3:\n",sess.run([op3,filter3])) #1-3
    # print("------------------")

    # print("op4:\n",sess.run([op4,filter4]))#2-2    通道叠加
    # print("op5:\n",sess.run([op5,filter5]))#2-1
    # print("------------------")


    print("op1:\n",sess.run([op1,filter1]))#1-1
    print("vop1:\n",sess.run([vop1,filter1]))
    print("op6:\n",sess.run([op6,filter1]))
    print("vop6:\n",sess.run([vop6,filter1]))

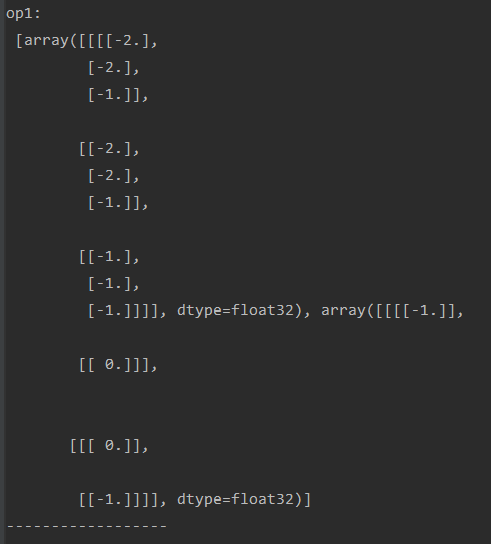
结果可以看出： 5x5 矩阵通过卷积操作生成了 3X3矩阵，对padding的补0情况是在后面和下面，所以会在矩阵的右边和下边生成-1.

结果可以看出：
对于 op1和vop1的比较可以看出， 5x5 矩阵在padding 模式为 'SAME'时生成 3x3 矩阵，而在 'VALID' 时生成 2x2.