java HashMap hash方法分析 - HelloWorld开发者社区

下面分别分析下，JDK1.7 与 JDK1.8 中 hash方法的运算过程，并且左后结合JDK1.8 中 hash方法来进行详细说明。

JDK1.7 中HashMap 中hash table 定位算法：

int hash = hash(key.hashCode());

int i = indexFor(hash, table.length);

其中indexFor和hash源码如下：

/** * Applies a supplemental hash function to a given hashCode, which * defends against poor quality hash functions. This is critical * because HashMap uses power-of-two length hash tables, that * otherwise encounter collisions for hashCodes that do not differ * in lower bits. Note: Null keys always map to hash 0, thus index 0. */ static int hash(int h) { // This function ensures that hashCodes that differ only by // constant multiples at each bit position have a bounded // number of collisions (approximately 8 at default load factor). h ^= (h >>> 20) ^ (h >>> 12); return h ^ (h >>> 7) ^ (h >>> 4); }

/** * Returns index for hash code h. */ static int indexFor(int h, int length) { return h & (length-1); }

indexFor这个方法论坛中已有人分析过，这里就不再分析。

现在分析一下hash算法：

Java代码

h ^= (h >>> 20) ^ (h >>> 12);

return h ^ (h >>> 7) ^ (h >>> 4);

假设key.hashCode()的值为：0x7FFFFFFF，table.length为默认值16。
上面算法执行如下：

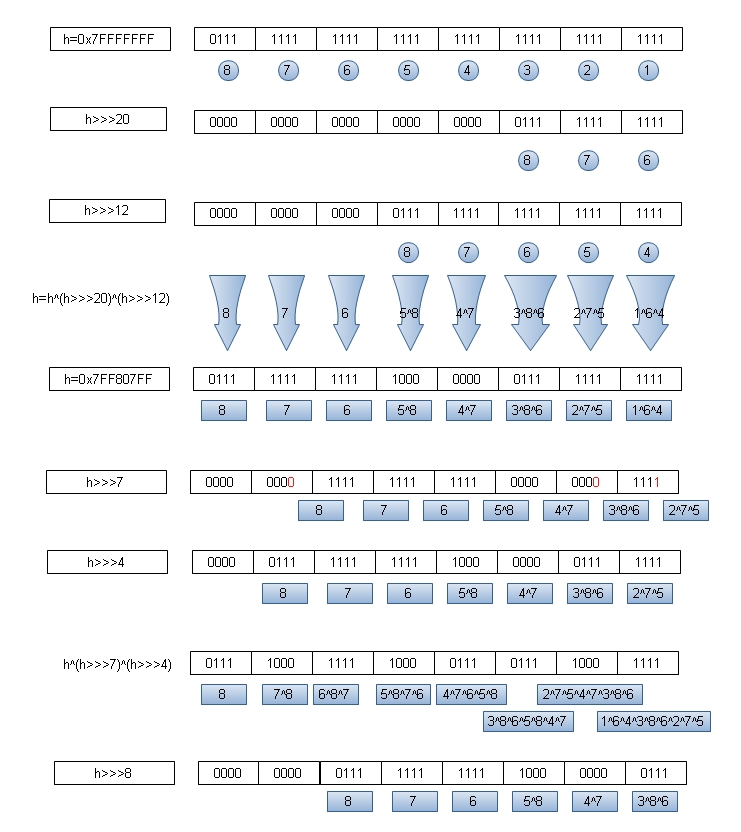
java HashMap hash方法分析

得到i=15

其中h^(h>>>7)^(h>>>4) 结果中的位运行标识是把h>>>7 换成 h>>>8来看。

即最后h^(h>>>8)^(h>>>4) 运算后hashCode值每位数值如下：
8=8
7=7^8
6=6^7^8
5=5^8^7^6
4=4^7^6^5^8
3=3^8^6^5^8^4^7
2=2^7^5^4^7^3^8^6
1=1^6^4^3^8^6^2^7^5
结果中的1、2、3三位出现重复位^运算
3=3^8^6^5^8^4^7     ->   3^6^5^4^7
2=2^7^5^4^7^3^8^6   ->   2^5^4^3^8^6
1=1^6^4^3^8^6^2^7^5 ->   1^4^3^8^2^7^5

算法中是采用(h>>>7)而不是(h>>>8)的算法，应该是考虑1、2、3三位出现重复位^运算的情况。使得最低位上原hashCode的8位都参与了^运算，所以在table.length为默认值16的情况下面，hashCode任意位的变化基本都能反应到最终hash table 定位算法中，这种情况下只有原hashCode第3位高1位变化不会反应到结果中，即：0x7FFFF7FF的i=15。

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

JDK1.8中hash方法已经得到了简化

static final int hash(Object key) { int h; return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); }

并且针对HashMap中的hash算法，大家看的一脸懵逼。这段代码叫“扰动函数”。

我们知道，HashMap通过 (length - 1) & hash 的方式获取table数组的下标，并且table的长度必须为2 ^ n，因为这样前面的公式就相当于取模。

如果我们对key的hash不进行扰动，“与”操作的结果就是hashcode的高位全部归0，只保留低位的值用来做数组下标访问。以初始长度16为例，16 - 1 = 15。2进制表示是00000000 00000000 00001111。和某散列值做“与”操作如下，结果就是借去了最低位的四位。

10100101 11000100 00100101

& 00000000 00000000 00001111

---------------------------------------------

00000000 00000000 00000101 // 高位全部归0，只保留末四位

但这个时候问题就来了，这样就算我的hashcode散列值再怎么松散，要是只取最后几位的话，碰撞也会很严重。更要命的是如果散列本身做的不好，分布上成等差数列的漏洞，恰好使最后几个低位呈现规律性重复，就无比蛋疼。

这时候扰动函数的价值就体现出来了，我们根据图来分析JDK1.8 的hash方法如何扰动的

java HashMap hash方法分析