Spark 系列（六）Spark - HelloWorld开发者社区

写在前面： 我是「nicedays」，一枚喜爱做特效，听音乐，分享技术的大数据开发猿。这名字是来自world order乐队的一首HAVE A NICE DAY。如今，走到现在很多坎坷和不顺，如今终于明白nice day是需要自己赋予的。
白驹过隙，时光荏苒，珍惜当下~~
写博客一方面是对自己学习的一点点总结及记录，另一方面则是希望能够帮助更多对大数据感兴趣的朋友。如果你也对 大数据与机器学习感兴趣，可以关注我的动态 https://blog.csdn.net/qq_35050438，让我们一起挖掘数据与人工智能的价值~

Spark GraphX 图算法：

一：PageRank模型：

每个网页为一个点

A到B的链接抽象为一条有向边

整张网页链接抽象成一份有向图

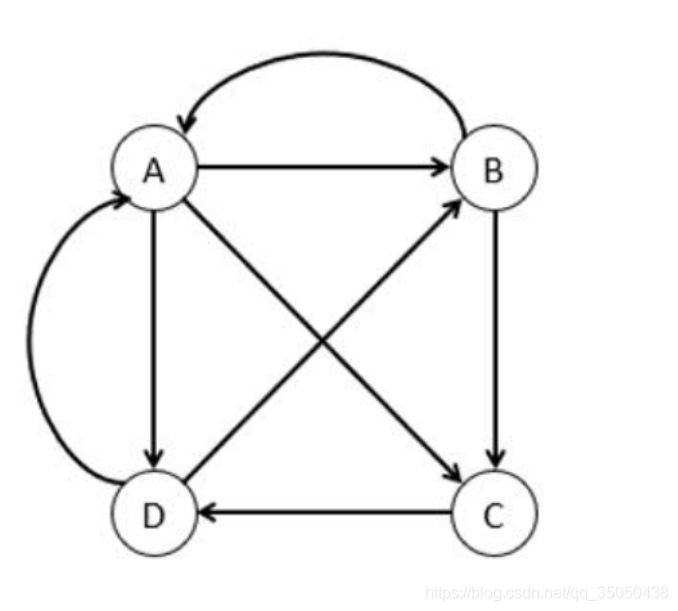
Spark 系列（六）Spark

接下来我们通过一个转移矩阵来表示用户从页面i到页面j的可能性

M = [ 0 1 2 0 1 2 1 3 0 0 1 2 1 3 1 2 0 0 1 3 0 1 0 ] M = \begin{bmatrix}0 & \frac{1}{2} & 0 & \frac{1}{2} \\\frac{1}{3} & 0 & 0 & \frac{1}{2} \\\frac{1}{3} & \frac{1}{2} & 0 & 0 \\\frac{1}{3} & 0 & 1 & 0\end{bmatrix} M=⎣⎢⎢⎡03131312102100001212100⎦⎥⎥⎤

这个矩阵的每一列代表一个具体网页的出链，简单地说就是当前网页向其他网页的链接，第一列为A-A,A-B,A-C,A-D
矩阵的每一行代表一个具体网页的入链，简单地说就是其他网页向当前网页的链接,第一行为A-A,B-A,C-A,D-A

Rank值：

不加权重的话，本意是当前页面点击一次后停留在自己页面的概率

初始时用户访问每个页面的概率均等，假设一共有 N 个网页，每个网页的初始 PR 值 = 1 / N。我们可以将这些网页的初始 PR 值保存到一个向量中。

P 0 = [ 1 4 1 4 1 4 1 4 ] T P_0 = \begin{bmatrix}\frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\\end{bmatrix}^T P0=[41414141]T

现在我们需要求根据当他点击一次继续停留在当前页面的概率

如果初始状态为B页面来说，当他点击一次继续停留在A页面的概率我们应该这样考虑：

情况一：B页面是从A走到B的，同时点击一次继续留在该页面，

两个事件必须同时发生，第一个事件发生概率为1/3,第二个事件发生概率为1/4
P ( A B ) = P ( A ) P ( B ) P(AB) = P(A)P(B) P(AB)=P(A)P(B)

所以情况一概率为1/12
情况二：B页面是从D走到B的，同时点击一次继续留在该页面，

两个事件必须同时发生，第一个事件发生概率为1/2,第二个事件发生概率为1/4,同理情况二概率为1/8

总概率为两个情况之和：5/24

所有的页面停留概率可以用矩阵相乘来得到：
P 1 = M ∗ P 0 = [ 0 1 2 0 1 2 1 3 0 0 1 2 1 3 1 2 0 0 1 3 0 1 0 ] ∗ [ 1 4 1 4 1 4 1 4 ] = [ 1 4 5 24 5 24 1 3 ] P_1 = M*P_0=\begin{bmatrix}0 & \frac{1}{2} & 0 & \frac{1}{2} \\\frac{1}{3} & 0 & 0 & \frac{1}{2} \\\frac{1}{3} & \frac{1}{2} & 0 & 0 \\\frac{1}{3} & 0 & 1 & 0\end{bmatrix}*\begin{bmatrix}\frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \end{bmatrix}=\begin{bmatrix}\frac{1}{4} \\ \frac{5}{24} \\ \frac{5}{24} \\ \frac{1}{3} \\ \end{bmatrix} P1=M∗P0=⎣⎢⎢⎡03131312102100001212100⎦⎥⎥⎤∗⎣⎢⎢⎡41414141⎦⎥⎥⎤=⎣⎢⎢⎡4124524531⎦⎥⎥⎤
每乘以1/4的向量相当于我计算每点击一次继续停留在该页面的概率，在不断点击迭代后，由于马尔科夫性，最终会收敛到一个值。

二：终止点问题：

先前所举的例子是一个理想状态：

假设所有网页组成的有向图是强连通的，即从一个网页可以到达任意网页。但实际的网络链接环境没有这么理想，有一些网页不指向任何网页，或不存在指向自己的链接。
Spark 系列（六）Spark

如果存在没有出度的点，那么当我们不断迭代上面的矩阵方程时，最终一定会收敛于0，也就是最后大家都会跳到那个没有出度的点上。

三：陷阱问题：

陷阱指的是只有指向自身链接的网页

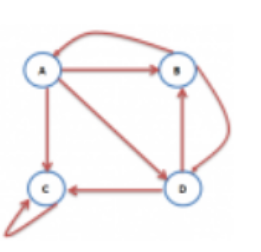
Spark 系列（六）Spark

上网者浏览到 C 网页将陷入无休止的循环之中
M = [ 0 1 2 0 0 1 3 0 0 1 2 1 3 0 1 1 2 1 3 1 2 0 0 ] M = \begin{bmatrix}0 & \frac{1}{2} & 0 & 0 \\\frac{1}{3} & 0 & 0 & \frac{1}{2} \\\frac{1}{3} & 0 & 1 & \frac{1}{2} \\\frac{1}{3} & \frac{1}{2} & 0 & 0\end{bmatrix} M=⎣⎢⎢⎡03131312100210010021210⎦⎥⎥⎤
根据公式
P n = M ⋅ P n − 1 = M n ⋅ P 0 P_n=M⋅P_{n−1}=M^n⋅P_0 Pn=M⋅Pn−1=Mn⋅P0
迭代计算出 PR 值向量。

四：阻尼系数：

我们可以通过阻尼系数来解决陷阱问题和孤立点问题了。

随即浏览模型：

假定一个上网者从一个随机的网页开始浏览，此时有两种选择：

通过点击当前页面的其他链接开始下一次浏览。
通过在浏览器的地址栏输入新的地址以开启一个新的网页。

由此，上网者从点击链接来跳转的概率变为d，此时PageRank模型变为：在每一个页面，用户都有d概率点击链接，1-d概率输入地址栏跳转，而输入地址栏跳转到任一页面的概率为1/N（N为页面）。
P n = d ∗ [ 0 1 2 0 1 2 1 3 0 0 1 2 1 3 1 2 0 0 1 3 0 1 0 ] ∗ [ 1 4 1 4 1 4 1 4 ] + ( 1 − d ) ∗ [ 1 4 1 4 1 4 1 4 ] P_n = d*\begin{bmatrix}0 & \frac{1}{2} & 0 & \frac{1}{2} \\\frac{1}{3} & 0 & 0 & \frac{1}{2} \\\frac{1}{3} & \frac{1}{2} & 0 & 0 \\\frac{1}{3} & 0 & 1 & 0\end{bmatrix}*\begin{bmatrix}\frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \end{bmatrix} + (1-d)*\begin{bmatrix}\frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \frac{1}{4} \\ \end{bmatrix} Pn=d∗⎣⎢⎢⎡03131312102100001212100⎦⎥⎥⎤∗⎣⎢⎢⎡41414141⎦⎥⎥⎤+(1−d)∗⎣⎢⎢⎡41414141⎦⎥⎥⎤

而阻尼系数d我们经过实验测算一般归纳为0.85

五：PageRank in GraphX

PageRank（PR）算法
- 用于评估网页链接的质量和数量，以确定该网页的重要性和权威性的相对分数，范围为0-10
- 从本质上讲，PageRank是找出图中顶点（网页链接）的重要性
- GraphX提供了PageRank API用于计算图的PageRank

Spark实现PageRank：

import org.apache.spark.HashPartitioner
 
val links = sc.parallelize(List(("A",List("B","C")),("B",List("A","C")),("C",List("A","B","D")),("D",List("C")))).partitionBy(new HashPartitioner(100)).persist()
 
var ranks=links.mapValues(v=>1.0)
 
for (i <- 0 until 10) {
val contributions=links.join(ranks).flatMap {
case (pageId,(links,rank)) => links.map(dest=>(dest,rank/links.size))
}
ranks=contributions.reduceByKey((x,y)=>x+y).mapValues(v=>0.15+0.85*v)
}
 
ranks.sortByKey().collect()

PageRank 算法缺点

主题漂移问题：PageRank 算法仅利用网络的链接结构，无法判断网页内容上的相似性；且算法根据向外链接平均分配权值使得主题不相关的网页获得与主题相关的网页同样的重视度，出现主题漂移。
没有过滤广告链接和功能链接：例如常见的“分享到微博”，这些链接通常没有什么实际价值，前者链接到广告页面，后者常常链接到某个社交网站首页。
对新网页不友好：一个新网页的入链相对较少，即便它的内容质量很高，但要成为一个高 PR 值的页面仍需要很长时间的推广。