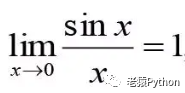一、极限的定义及四则运算
极限:某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值A不断地逼近而“永远不能够重合到A”(“永远不能够等于A,但是取等于A‘已经足够取得高精度计算结果)的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近A点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值A叫做“极限值”
ε-δ(epsilon-delta)语言:epsilon-delta语言是用来描述函数极限的语言,其描述如下:
对于任意ε>0,存在δ>0,当0<丨x-x0丨<δ时,有丨f(x)-L丨<ε。即x无限靠近x0时则函数f(x)的极限为L,记为: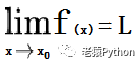
ε-N语言:用于描述数列的极限,其描述如下:
所谓xn→x,就是指:“如果对任何ε>0,总存在自然数N,使得当n>N时,不等式|xn-x|<ε恒成立”。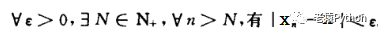
极限的四则运算

无穷小的运算

极限的复合运算
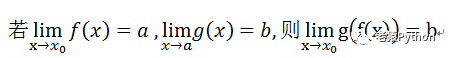
等价无穷小

- 需要熟记的几个函数极限
※ limC = C,C为常数
※ limCf(x) = Clim f(x),C为常数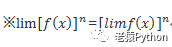
二、级数
级数是指将数列的项依次用加号连接起来的函数,级数理论是分析学的一个分支;它与另一个分支微积分学一起作为基础知识和工具出现在其余各分支中。二者共同以极限为基本工具,分别从离散与连续两个方面,结合起来研究分析学的对象,即变量之间的依赖关系──函数;
级数是指将数列Un的项U1、U2 ,…,Un,…依次用加号连接起来的函数,是数项级数的简称。这些项的和简写为ΣUn,Un称为级数的通项。如果当n→∞ 时 ,数列Un有极限,则说级数收敛,并以 S为其和,记为 ΣUn= S;否则就说级数发散。
级数1/n是发散的,级数n的a次方(a为大于1的整数)之一(即通项的分母是n的a次方)是收敛的 ;
在n和a为大于1的整数情况下,下来通项对应的级数的大小及收敛、发散性排列如下:
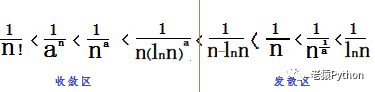
上图红线左边的级数是收敛的,右边的级数是发散的,当然红线两边的级数之间还可以在两区插入更多符合条件的级数。
三、函数的连续性
3.1、定义
连续函数是指函数y=f(x)当自变量x的变化很小时,所引起的因变量y的变化也很小。对于这种现象,因变量关于自变量是连续变化的,连续函数在直角坐标系中的图像是一条没有断裂的连续曲线。由极限的性质可知,一个函数在某点连续的充要条件是它在该点左右都连续。
一个函数在开区间(a,b) 内每点连续,则为在(a,b) 连续,若又在 a点右连续, b点左连续,则在闭区间[a,b]连续,如果在整个定义域内连续,则称为连续函数。由极限的性质可知,一个函数在某点连续的充要条件是它在该点左右都连续。如果x在x0处的左极限和右极限不相等,则f(x)在x0处不连续。一切连续函数在其定义区间内的点都连续。
3.2、间断点

3.3、连续函数法则
定理一 在某点连续的有限个函数经有限次和、差、积、商(分母不为0) 运算,结果仍是一个在该点连续的函数
定理二 连续单调递增 (递减)函数的反函数,也连续单调递增 (递减)
定理三 连续函数的复合函数是连续的。
3.4、重要特性
有界性:闭区间上的连续函数在该区间上一定有界,所谓有界是指,存在一个正数M,使得对于任意x∈[a,b],都有|f(x)|≤M
最值性:闭区间上的连续函数在该区间上一定能取得最大值和最小值,所谓最大值是指,[a,b]上存在一个点x0,使得对任意x∈[a,b],都有f(x)≤f(x0),则称f(x0)为f(x)在[a,b]上的最大值。最小值可以同样作定义,只需把上面的不等号反向即可。
介值性:若f(a)=A,f(b)=B,且A≠B。则对A、B之间的任意实数C,在开区间(a,b)上至少有一点c,使f( c )=C。它包含了两种特殊情况:
(1)零点定理。
也就是当f(x)在两端点处的函数值A、B异号时(此时有0在A和B之间),在开区间(a,b)上必存在至少一点ξ,使f(ξ)=0。
(2)闭区间上的连续函数在该区间上必定取得最大值和最小值之间的一切数值。一致连续性:闭区间上的连续函数在该区间上一致连续。
所谓一致连续是指,对任意ε>0(无论其多么小),总存在正数δ,当区间I上任意两个数x1、x2满足|x1-x2|<δ时,有|f(x1)-f(x2)|<ε,就称f(x)在I上是一致连续的。反函数连续性:如果函数f在其定义域D上严格单调且连续,那么其反函数g也在其定义域f(D)(即f的值域)上严格单调且连续
写博不易,敬请支持:
如果阅读本文于您有所获,敬请点赞、评论、收藏,谢谢大家的支持!
更多人工智能数学基础的介绍请参考专栏《人工智能数学基础 》
本文转转自微信公众号老猿Python原创https://mp.weixin.qq.com/s/EXaKB14FQ-2mxCJBpsCXAw,如有侵权,请联系删除。