作者:京东零售 周佳慧
背景
大家在做实验时有没有遇到过以下的问题?
实验分流不太稳定,多次分流以后,发现随机分组历史数据指标波动特别大 实验结果不符合预期,在去掉几个特殊用户后结果变化较大、甚至正负反转 不同的业务场景设置的指标过滤规则不同,例如A场景过滤掉了成单超过100单的用户、但B场景没有过滤,实验指标应该选择哪个
这里实验者大概率是遇到了实验中的异常值问题,我们接下来会讨论在互联网AB实验场景中,应该如何进行处理?
概念解析
从严格的学术角度来看,异常值并没有一个统一的定义和划分标准,在不同的领域会根据使用目的和数据特点有不同的定义逻辑和检验方法。即我们可以得到“在一个样本或集合中,与其余样本均有较大差异的样本点就是异常值”这样一个通用、模糊的概念,但具体差异较大的判定标准是什么,检测差异的方法有哪些,场景之间各不相同。
举个例子,很多人都听说过的3sigma原则指的是:如果一个样本取值超过了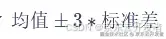
这个范围,那么就属于异常值。但这个标准通常假设了样本的分布属于正态分布或者近似正态分布,对于互联网公司的幂律分布指标适用性较差,我相信大家都能感受到“JD大盘Top1%的用户成单GMV都是异常值”这个结论有多么的离谱。
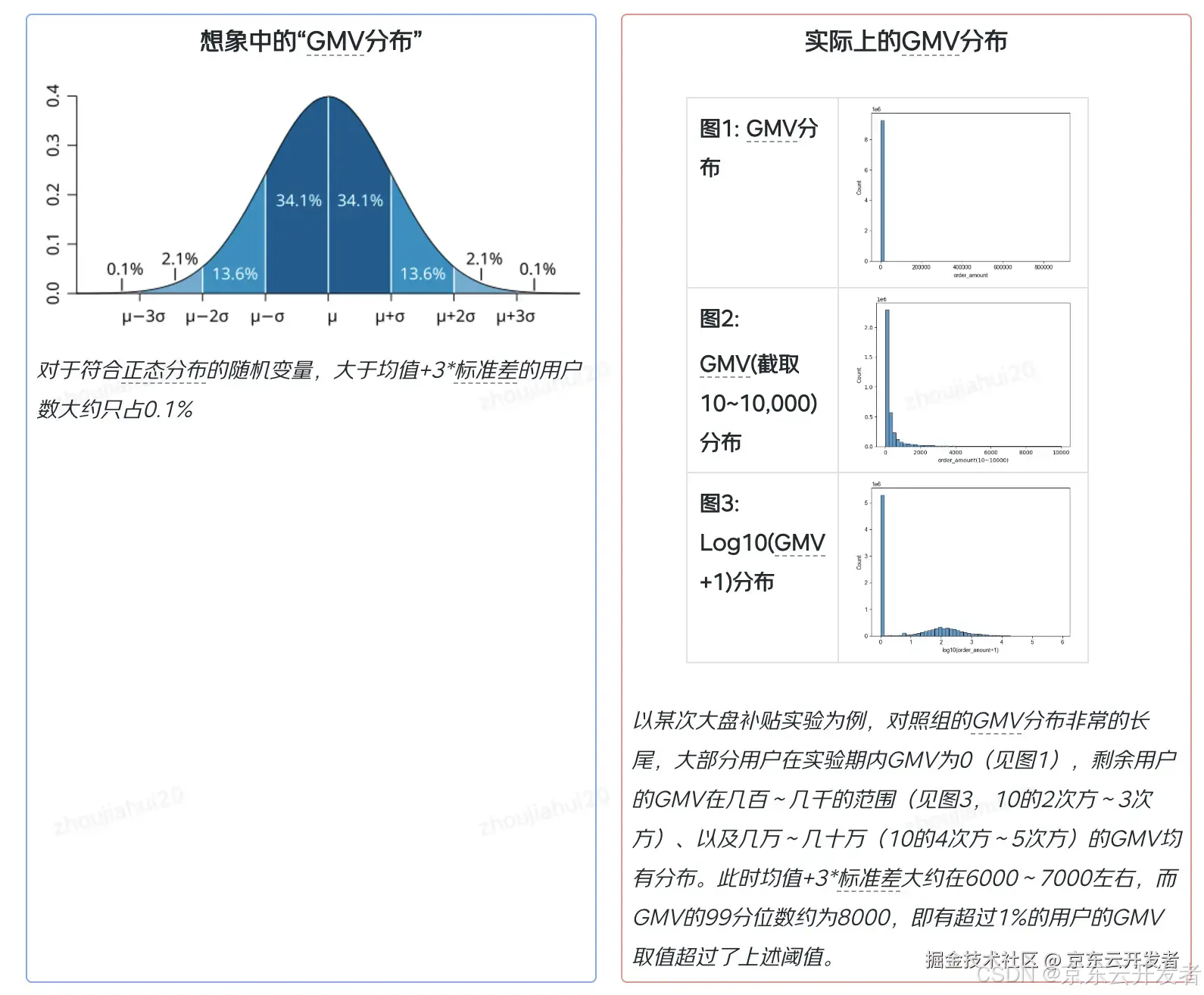
基于上述思考,后续研究中我们会着重研究在大样本、幂律分布等和互联网AB实验面临状况比较相似的情况,并参考比如调研分析、社会学等直接收集人类社会经济活动数据的学术分枝统计方法,以及新兴的算法方向的异常值检测、处理方法。
异常值产生的基本原因
•数据收集过程中的测量误差(工具误差)
•群体中个体的差异性(抽样带来的随机性)
•数据造假、作弊(刷单)
•收集的样本来源于不同的群体(比如京东App中有很多背后是B端的用户)
AB实验中异常值剔除的作用与局限性
1.为什么AB实验需要进行异常值处理?
•有一小部分异常用户,由于数据分布非常异常,造成了分流时无法将这一批用户每一次都很完美的均匀分布在实验组、对照组,异常用户在哪、哪个组就会出现AA不均匀的情况
•由于异常用户的指标值较大,造成了整体指标的波动性较大,让实验的精度变差、样本量需求变大,原本可以观测的实验效果就会被淹没在噪音中(指标方差较大带来实验最小提升量-MDE较大)
2.异常值剔除方案的局限性
•做不到的:无法识别业务逻辑中认定的异常值以及异常用户(比如xx用户命中了xx风控规则,所有数据不可信),无法识别指标统计错误(比如某用户1天内在一个页面的停留时长超过24H)
•能做但做不好的:降低指标的波动性,但同时可能会去掉了部分有效样本和有效数据,会让样本产生偏差(bias)。此时需要用更多的样本才能进行更灵敏的实验,或使用ANCOVA、CUPED等方差缩减的方法。
传统统计学方法的应用—— trim & winsorize方法对于补贴实验的效果对比
1.什么是trim方法与winsorize方法,为什么选择这些方法?
这两种方法其实源自于上个世纪的调研分析方法,当年的统计学家除了会遇到样本量不足的问题外,也会遇到在样本收集、统计过程中发生错误而导致的异常值。在当年各种算法技术、算力限制的情况下,统计学家会通过观察、处理当前数据指标分布的方式,对样本进行更加稳健的估计。具体来看
◦Winsorizing(或缩尾法):当样本点的取值超过样本的特定分位数后,将取值直接替换为分位数值
◦Trimming(或去尾法):当样本点的取值超过样本的特定分位数后,将样本点直接丢弃
2.数据表现
•我们使用异常值处理后对样本均值、标准差的影响作对比,可以发现在同样的分位数下,trimming方法通常会有更大的效果。
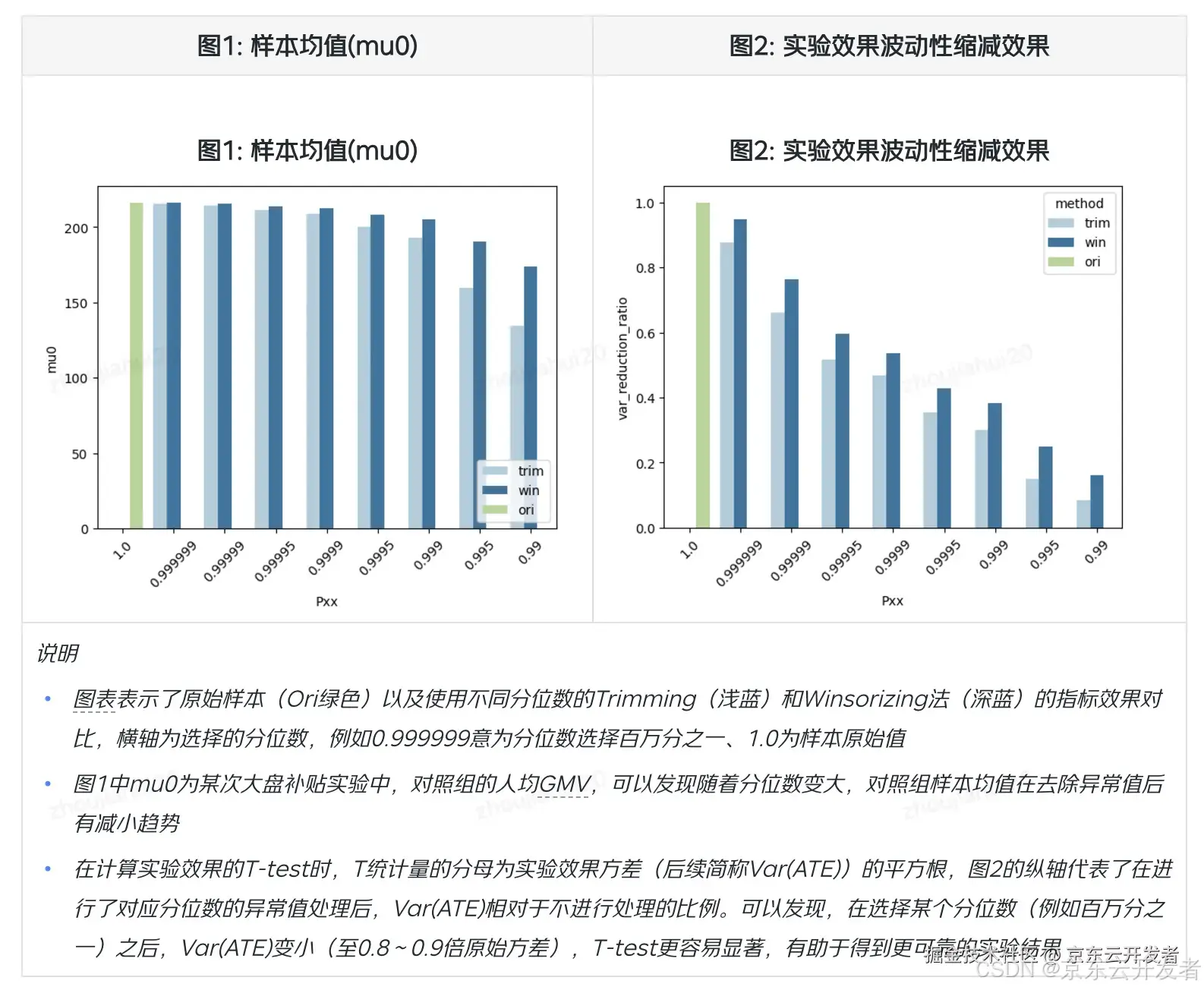
•但如果我们忽略掉具体的分位数选择,直接对比方法的损失(横轴,均值估计偏差)与收益(纵轴,方差缩减效果),可以发现winsorize方法更具有优势,即在相同的均值估计偏差下,有更大的方差缩减效果(即下图中,左下角更好)。
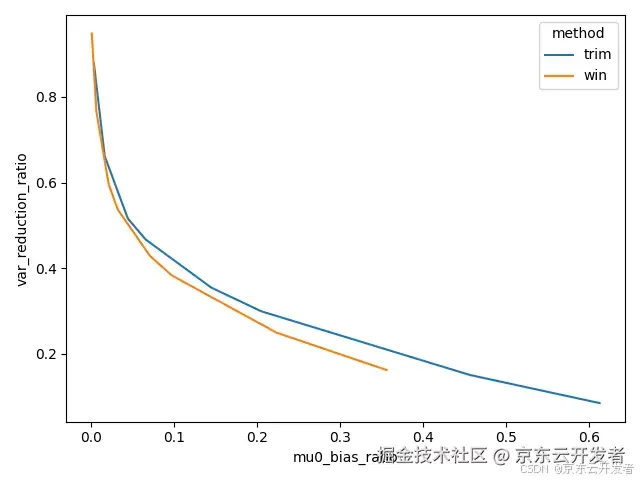
•方法对于实验的一类、二类错误影响如下👇
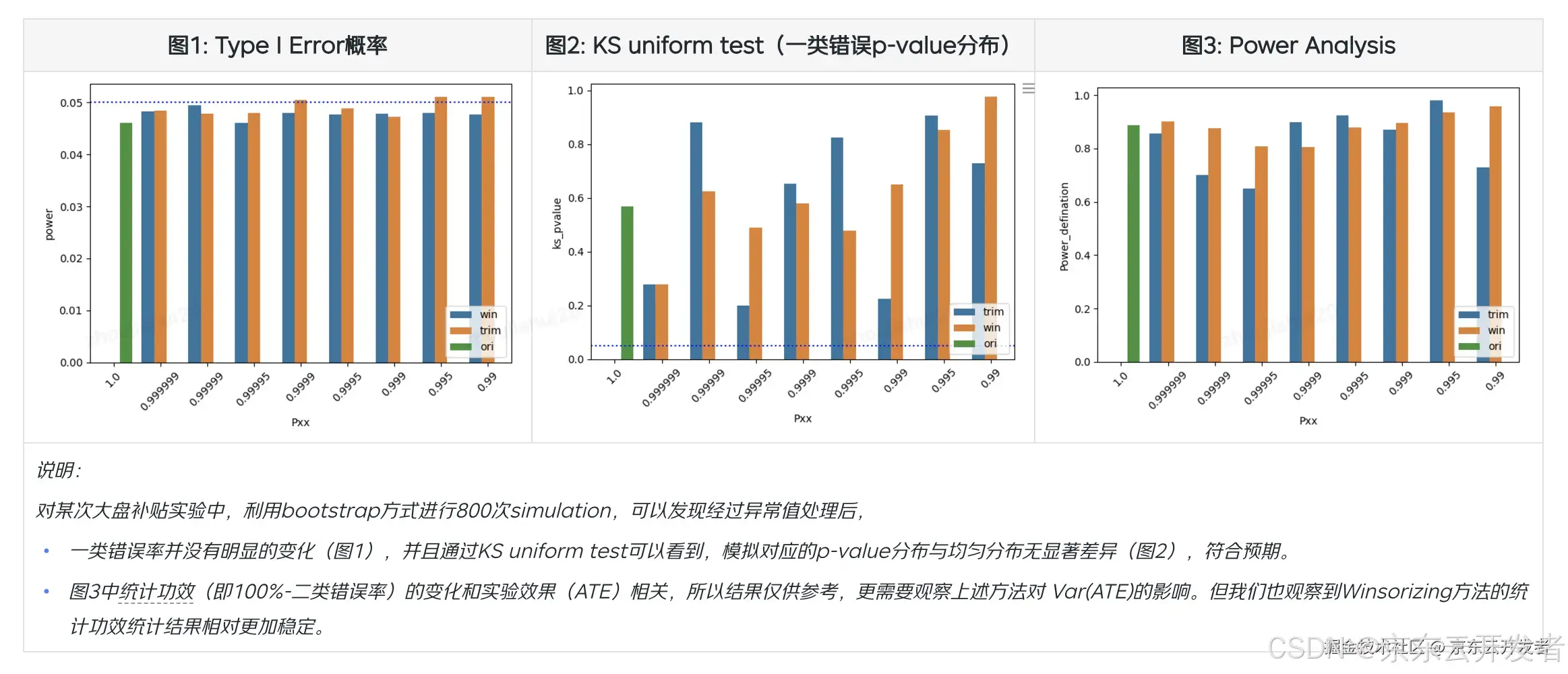
3.方案原理、效果对比
•在我们认为实验收集到的样本基本都是正常数据,只是分布比较分散时,不要轻易丢弃样本点,以防止损失样本对应的信息,此时Winsorizing(或缩尾法)相对是一个更加稳健的做法
•当样本中包含了很多脏数据和异常用户时(例如作弊、刷单用户),他们带来的信息会将会影响到样本的分布状态,那么使用trimming方法去掉他们会尽可能减弱此类影响
•在没有很多的业务输入情况下,可以根据数据的分布特征,并用winsorizing方法进行相对保守的异常值处理。
4.业务落地建议
•对于不同场景、不同类型的指标,业务需要根据自身场景特点,尽量排除脏数据、刷单作弊数据等异常情况
•对于本场景的重点指标,可以由分析人员进行一次性的分析,在得到合理的处理方案后可以尝试固化在实验平台
风控模型的应用
风控模型在内容时长指标异常值处理的应用👇
例:某实验在2024-09-30对照组出现人均时长指标异常增加的情况,影响实验观测。
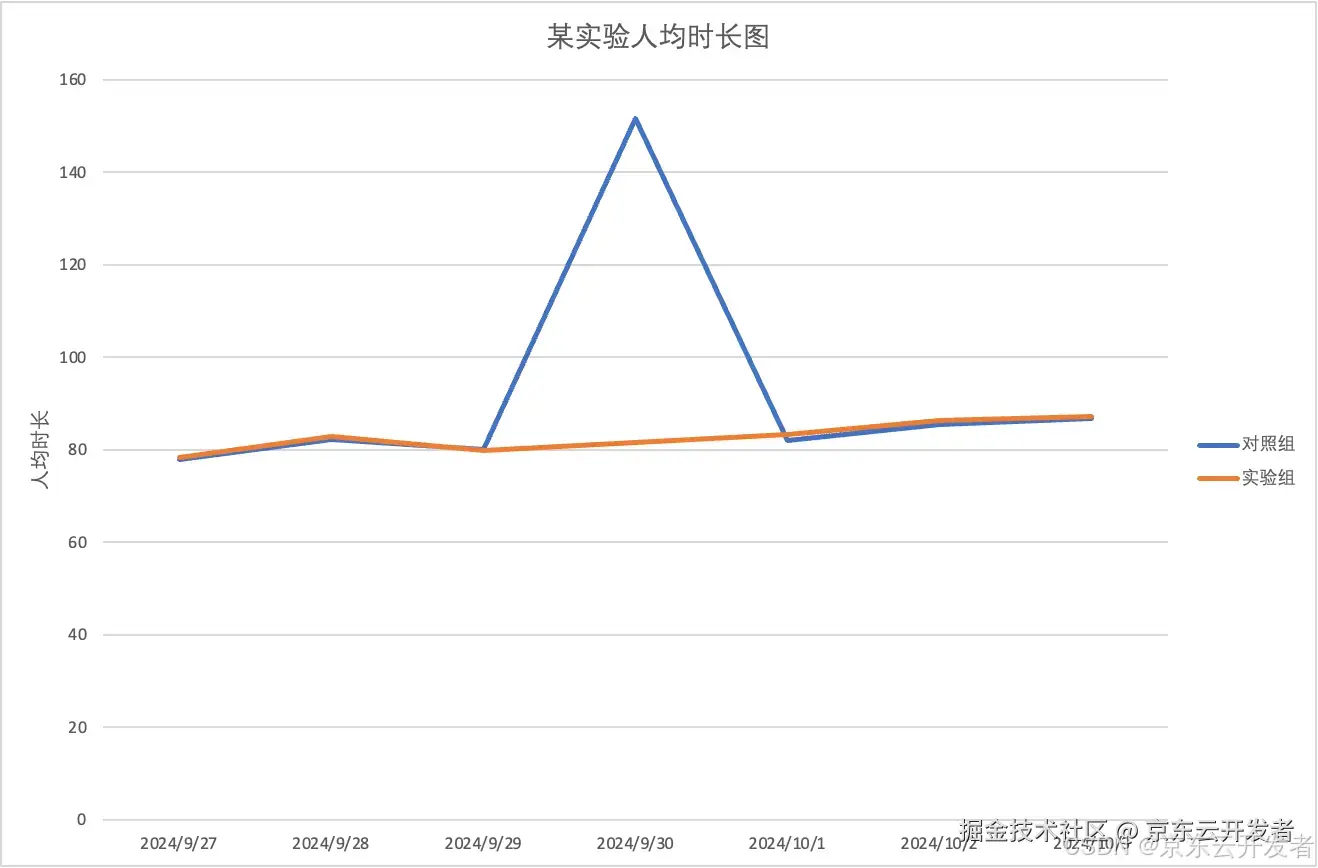
注:数据已经做脱敏处理
通过排查发现若干异常用户的作弊行为,反馈风控团队进行剔刷。剔刷后,作弊用户数据有效减少。另一方面,从实验信息上报的角度,采用服务端上报也可以从一定程度避免异常用户进入实验,减少异常值,让实验数据更可靠。
一些异常值检测方法的介绍
从实验平台功能建设上,往往采用计算量较小的较为通用的方案;一种适用于实验平台的异常值检测方法:当峰度大于某个阈值时,取 top x%极大值作为异常样本。其核心思想是根据数据分布判断是否需要进行异常值处理,然后通过分位数划定异常样本范围。
•峰度:对实值随机变量的概率分布的尾部的度量,峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。峰度计算公式如下: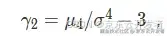 )其中
)其中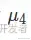 表示四阶矩。
对于特定的数据,Z-score等简单方法效果不佳时,我们也可以使用较为复杂的方法进行处理。下面是一些异常值检测方法的简单
表示四阶矩。
对于特定的数据,Z-score等简单方法效果不佳时,我们也可以使用较为复杂的方法进行处理。下面是一些异常值检测方法的简单
| 方法 | 基本原理 | 优点 | 缺点 | |
|---|---|---|---|---|
| 统计和概率模型 | 箱线图 | 基于1.5倍IQR划定异常值阈值。 | 直观、简便。 | 自适应较差,对于部分数据分布会完全失效。 |
| Z-score方法 | 基于数据标准化变换得到Z-score。正态分布可基于3sigma原则判断;一般分布可基于Chebyshev不等式;样本有界可基于Hoeffding不等式;对于高维空间,可基于样本与均值的马氏距离计算Z-score。 | 直观、简便。 | 样本统计量的估计受异常值影响;3sigma原则要求总体需服从正态分布;Chebyshev不等式需要合理选取阈值;高维空间需要矩阵求逆,计算量较大。 | |
| Grubbs方法 | 基于样本的均值、最大值和最小值进行异常值检验。 | 避免方差受异常值干扰的影响。 | 通常只适用于小样本。 | |
| 基于方差贡献 | 寻找样本子集,使得样本在移除该子集前后基于方差定义的损失函数。 | 直观、简便。 | 直接计算子集无法在多项式时间内求解, 需要启发式算法,计算量较大。 | |
| EM算法 | 可基于给定先验分布和群数计算各样本点分布的概率密度,基于概率密度判断异常值。 | 能够解决一般方法的打分阈值难选择的问题。 | 需要比较强的先验假设,计算量较大。 | |
| 绝对离差中位数 | 计算绝对离差。取其中位数,衡量异常值。 | 由于使用中位数,可以有效对抗异常值带来的影响。 | 自适应较差,对于部分数据分布会完全失效。 | |
| 基于机器学习算法 | ODIN/LOF/LOCI | 基于距离或者密度估计的异常值检测方法。 | 有一定的自适应性,能够根据相对疏密程度判断异常值 | 计算量较大。 |
| 直方图/Parzen窗函数概率密度估计 | 使用给定的分布计算各个样本点附近生成概率,加和构成估计的概率密度函数。 | 直观,简便,没有对分布的先验假设。 | 窗宽度是一个超参数,计算量较大。 | |
| 基于回归残差 | 基于先验知识拟合特征间的回归曲线,并基于拟合残差判定异常值,有时为了避免异常值对拟合结果产生影响,可以进行抽样。 | 直观,简便,在先验知识正确的前提下,检测结果较好。 | 需要较强的先验假设,异常值对回归拟合可能产生较大影响。 | |
| PCA | 将n维数据投影至k维平面上,在中心化的数据中,剩余k维向量范数较大的样本被判定为异常值。 | 可处理高维流行空间的异常值问题。 | 超参数k难以选择,如果需要使用PCA,核函数的选择需要先验知识。 | |
| 矩阵分解 | 将原矩阵分解为两个低秩矩阵,并将原数据用这两个低秩矩阵表出,将残差较大的样本判定为异常值。PCA本质上也可以理解为一种矩阵分解方法。 | 能够处理数据缺失问题。 | 仅适用于线性情况。 | |
| autoencoder | 使用给定数据训练自编码器,其编码器部分可以视作非线性降维方法,通过比较autoencoder的输入和输出差异,进行异常值判别。 | 引入非线性,通过自监督方式解决异常值检测缺乏训练标签的问题。 | 计算量较大。 | |
| One-Class SVM | 将所有样本视为1类,基于软间隔最大化训练支持向量机,并将跨过分隔平面的样本判定为异常值。 | 可通过核函数引入非线性。 | 核函数计算量较大。 | |
| Isolation Forest | 通过无监督方法构造一颗或多棵树,通过节点深度衡量异常程度。 | 通过抽样方法构建子树,使方法具有很高的效率。通过峰度系数选择特征,可以进一步提升子空间选择效率。 | 阈值的选择通常较为困难,且对不同的情况需要选择不同的阈值。 | |
| Robust Random Cut Forest | 改进Isolation Forest,对于特征选择概率依赖于各个维度的range。 | 相比改进Isolation Forest,对于特征选择的效率更高。 | 阈值的选择通常较为困难,且对不同的情况需要选择不同的阈值。 |
附录
实验波动性和实验精确度的关系:在计算实验效果时,利用实验组、对照组的均值、方差、样本量可以进行实验效果的假设检验,公式如下:

其中,
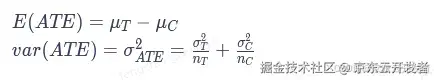
可以看到,如果实验的波动性(var(ATE))越大,在实验效果(E(ATE))不变的情况下,那T统计量就越小,实验就越不容易显著(精度较差);此时就需要减小var(ATE),即通过改变样本方差和样本量来减小样本波动性。