什么是索引?
索引是对数据库表中一列或多列的值进行排序的一种结构,使用索引可快速访问数据库表中的特定信息。
比如想从字典中查询某一个字,我们可以通过偏旁、或者拼音来快速定位到要找的页码,这种方式也可以被理解为一种索引。
Mysql常用的索引类型
类型
说明
Normal(普通)
普通索引,没任何限制。
Unique(唯一)
唯一索引要求健值不能重复。
Fulltext(全文)
针对比较大的数据,如商品详情,可以解决like查询效率低的问题。
索引的存储模型推演
索引是一种数据结构,那它到底是一种什么数据结构,才能实现数据的高效检索呢?
1. 二分查找
在给定一个有序数组中,如何以最快的方式找出给定的值? 有一点开发经验的第一个一定会想到使用二分查找方法进行查找。 比如有1到100的有序数组。另一个在中间想一个数,你猜的时候会告诉你高了,还是低了。
- 50? 高了
- 25?低了
- 37? 以上就是二分查找的一种思想,我们每次说一个数,就可以把结果范围缩小一半。如果数据是有序的话,这种方式效率比较高。
有序数据的等值查询和比较查询效率非常高,但是更新数据的时候会出现一个问题,可能要挪动大量的数据(改变Index),所以只适合静态数据。
为了支持频繁的修改,如插入,我们可以采用链表,但他的查找效率不够高。
所以有没有可以使用二分查找的链表呢?
2.二叉查找树(BST Binary Search Tree)
左子树所有的节点都小于父节点,右子树所有的节点都大于父节点。投影到平面以后,就是一个有序的线性表。 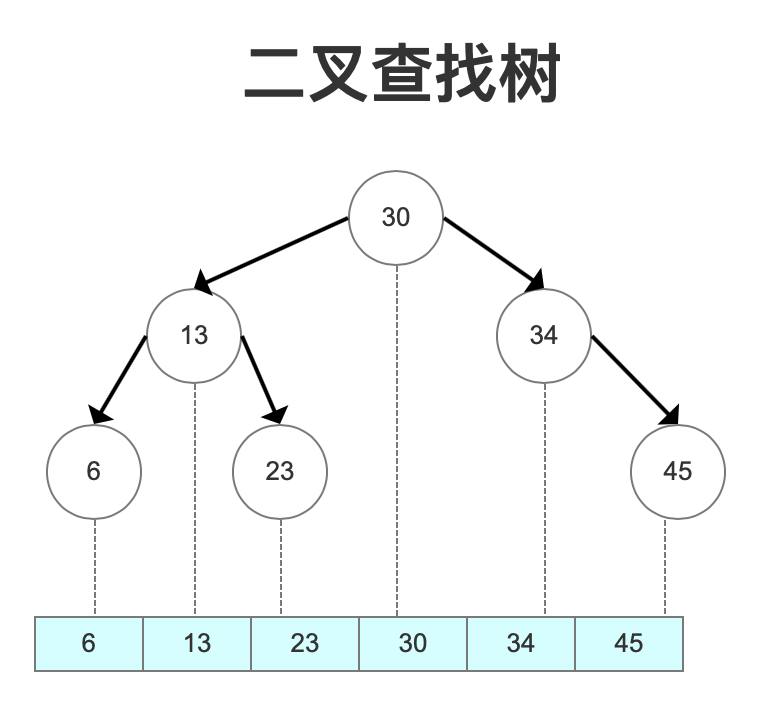
二叉树的特点:
左子树节点 < 父节点
右子树节点 > 父节点
二叉查找树既能够实现快速查找,又能够实现快速插入。
但是二叉查找树有一个问题:
就是它的查找耗时是和这棵树的深度相关的,在最坏的情况下时间复杂度会退化成O(n)。
什么情况是最坏的情况呢?
可以使用下边地址模拟:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
用上边的数据按6、13、23、30、34、45有序输入,就会发现这时候二叉树变成了一个《斜树》,这种情况下和顺序查找效率是没区别的。
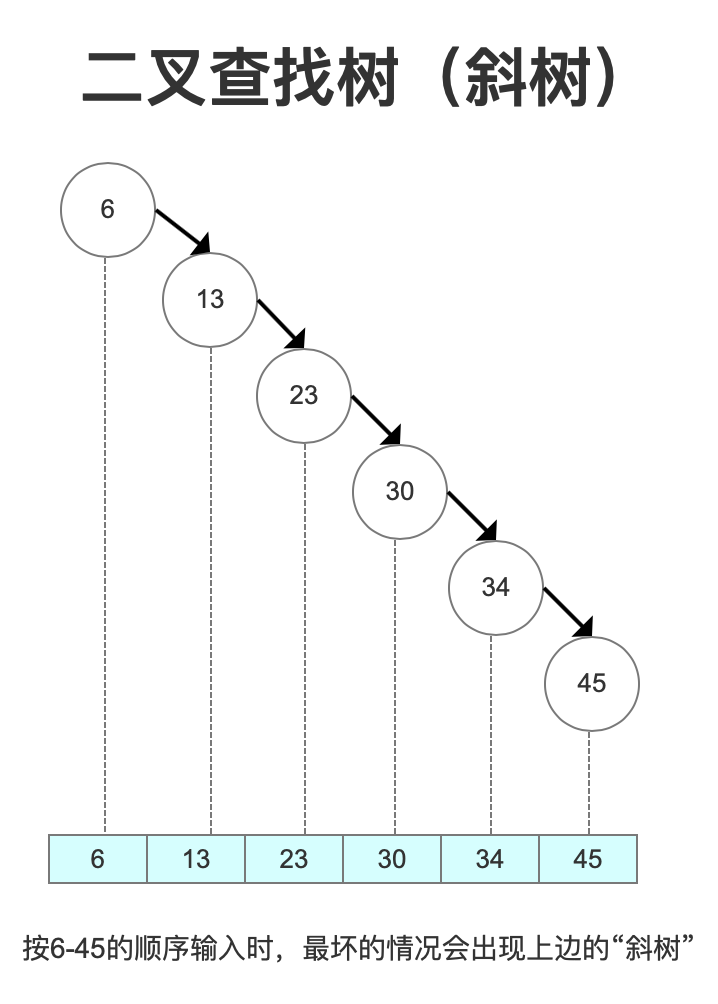
因为左右子树深度差太大,这棵树的左子树根本没有节点——也就是它不够平衡。
3. 平衡二叉树(AVL Tree)
平衡二叉树的定义:左右子树深度差绝对值不能超过1。
什么意思呢?比如左子树的深度是2,右子树的深度只能是1或者3。
还用上边的数据按6、13、23、30、34、45有序输入,一定不会再变成一棵《斜树》。
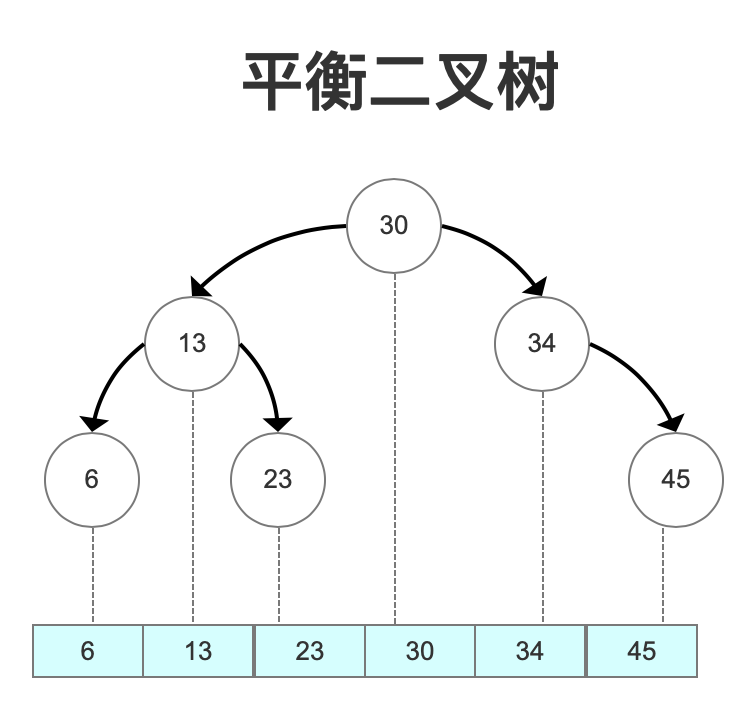
平衡的问题我们解决了,那么平衡二叉树作为索引怎么查询数据?
在平衡二叉树中,一个节点,它的大小是一个固定的单位,作为索引应该存储什么内容?
它应该存储三块的内容:
- 是索引的键值。比如我们在id上面创建了一个索引,我在用whereid=1的条件查询的时候就会找到索引里面的id的这个键值。
- 是数据的磁盘地址,因为索引的作用就是去查找数据的存放的地址。
- 因为是二叉树,它必须还要有左子节点和右子节点的引用,这样我们才能找到下一个节点。比如大于26的时候,走右边,到下一个树的节点,继续判断。
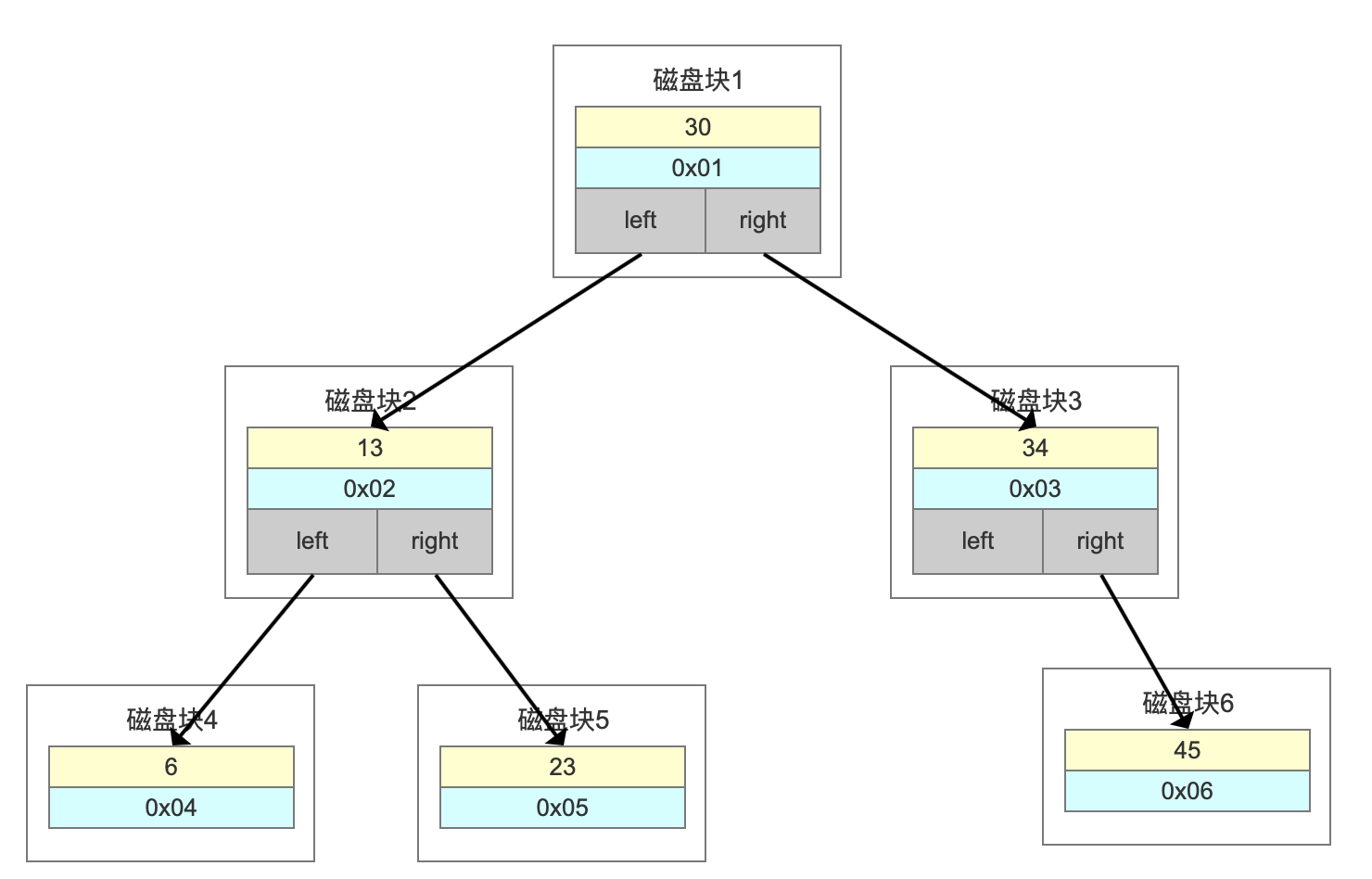
如果是这样存储数据的话,我们来看一下会有什么问题。
在分析用AVL树存储索引数据之前,我们先来学习一下InnoDB的逻辑存储结构。
InnoDB 逻辑存储结构
MySQL的存储结构分为5级:表空间、段、簇、页、行。
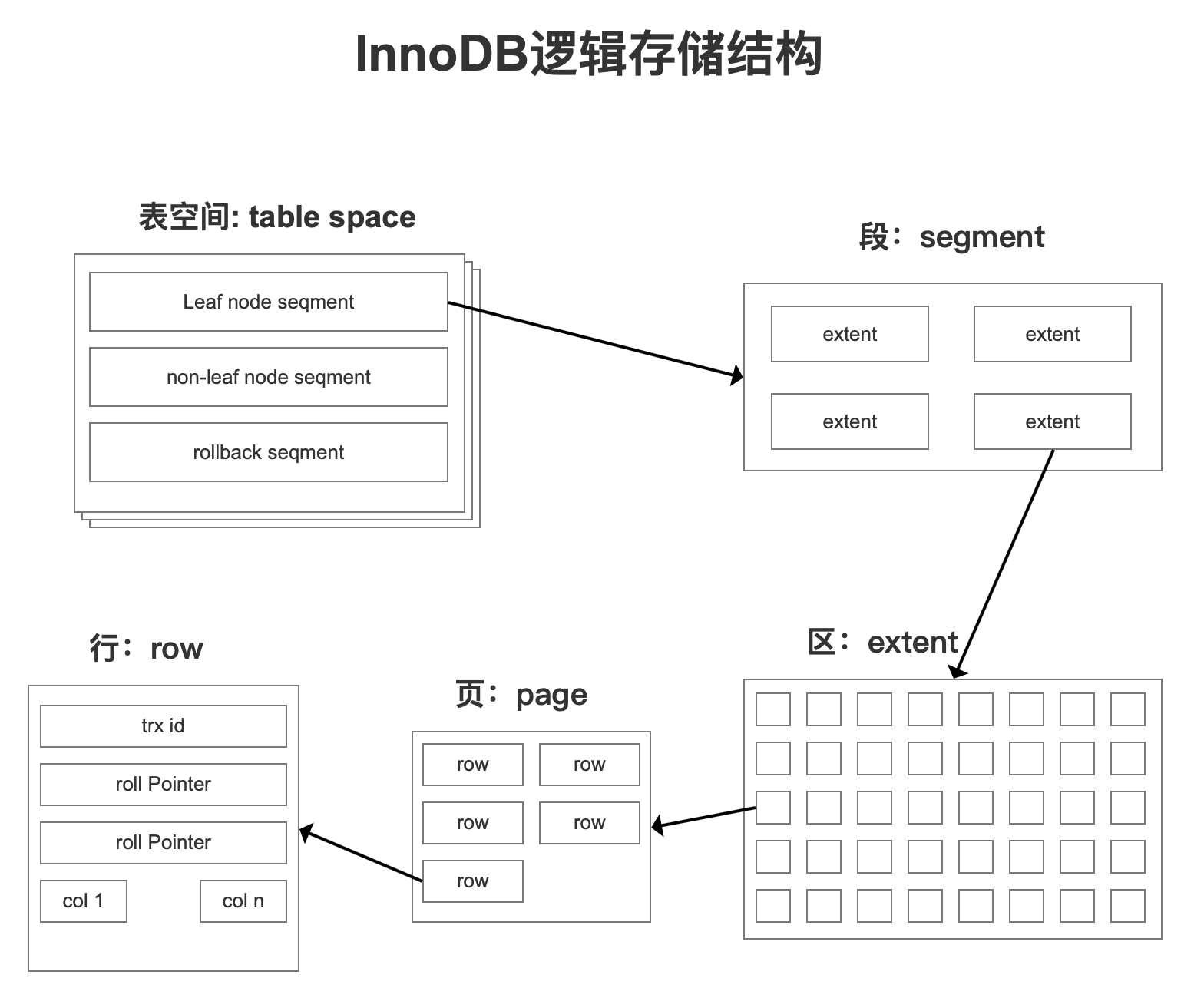
表空间 TableSpace
上一章讲磁盘结构的时候讲过了,表空间可以看做是InnoDB存储引擎逻辑结构的最高层,所有的数据都存放在表空间中。分为:系统表空间、独占表空间、通用表空间、临时表空间、Undo表空间。
段 Segment
表空间是由各个段组成的,常见的段有数据段、索引段、回滚段等,段是一个逻辑的概念。一个ibd文件(独立表空间文件)里面会由很多个段组成。
创建一个索引会创建两个段,一个是索引段:leaf node segment,一个是数据段:non-leaf node segment。索引段管理非叶子节点的数据。数据段管理叶子节点的数据。也就是说,一个表的段数,就是索引的个数乘以2。
簇 Extent
一个段(Segment)又由很多的簇(也可以叫区)组成,每个区的大小是1MB(64个连续的页)。
每一个段至少会有一个簇,一个段所管理的空间大小是无限的,可以一直扩展下去,但是扩展的最小单位就是簇。
页 Page
https://dev.mysql.com/doc/refman/5.7/en/innodb-row-format.html
为了高效管理物理空间,对簇进一步细分,就得到了页。簇是由连续的页(Page)组成的空间,一个簇中有64个连续的页。(1MB/16KB=64)。这些页面在物理上和逻辑上都是连续的。
跟大多数数据库一样,InnoDB也有页的概念(也可以称为块),每个页默认16KB。页是InnoDB存储引擎磁盘管理的最小单位,通过innodb_page_size设置。
一个表空间最多拥有2^32个页,默认情况下一个页的大小为16KB,也就是说一个表空间最多存储64TB的数据。
注意,文件系统中,也有页的概念。操作系统和内存打交道,最小的单位是页Page。文件系统的内存页通常是4K。
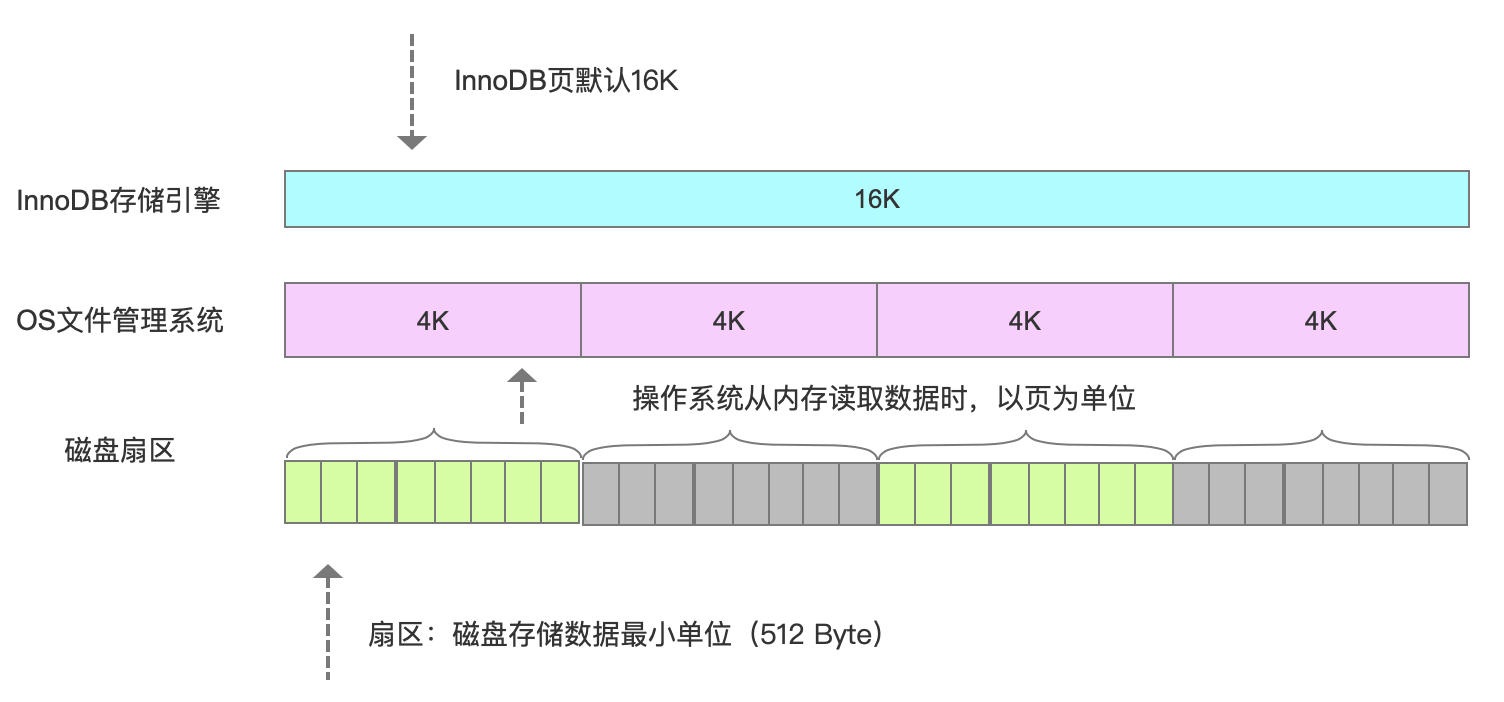
假设一行数据大小是1K,那么一个数据页可以放16行这样的数据。
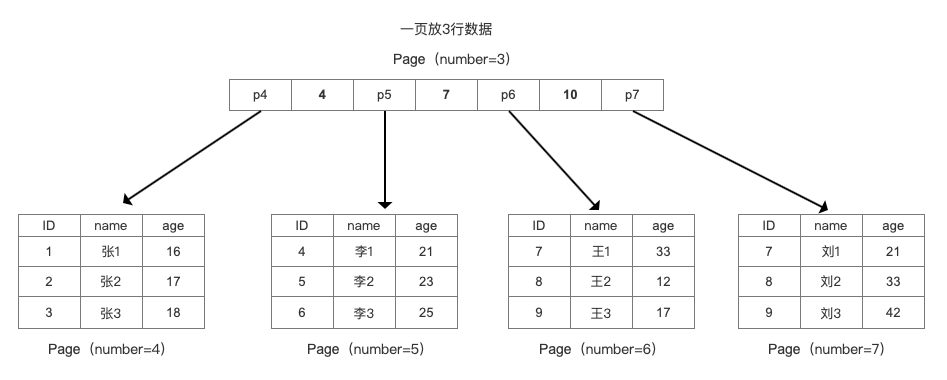
往表中插入数据时,如果一个页面已经写完,产生一个新的叶页面。如果一个簇的所有的页面都被用完,会从当前页面所在段新分配一个簇。
如果数据不是连续的,往已经写满的页中插入数据,会导致叶页面分裂:
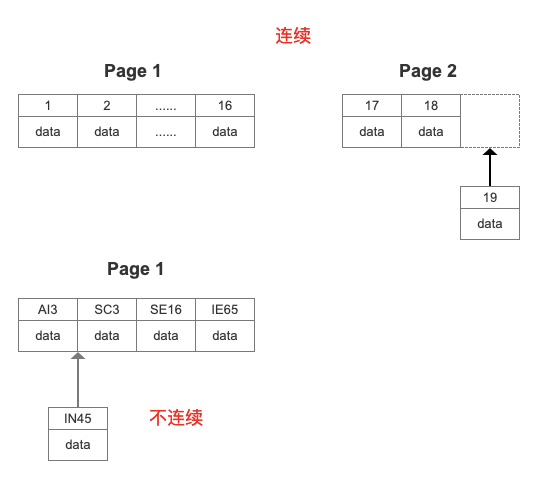
行 Row
InnoDB存储引擎是面向行的(row-oriented),也就是说数据的存放按行进行存放。
Antelope[ˈæntɪləʊp](羚羊)是InnoDB内置的文件格式,有两种行格式:
REDUNDANT[rɪˈdʌndənt] Row Format COMPACT Row Format(5.6默认)
Barracuda[ˌbærəˈkjuːdə](梭子鱼)是InnoDB Plugin支持的文件格式,新增了两种行格式:
文件格式
行格式
描述
Antelope(Innodb-base)
ROW_FORMAT=COMPACT
Compact和redumdant的区别在就是在于首部的存存内容区别。compact的存储格式为首部为一个非NULL的变长字段长度列表。
--
ROW_FORMAT=REDUNDANT
redundant的存储格式为首部是一个字段长度偏移列表(每个字段占用的字节长度及其相应的位移)。在Antelope中对于变长字段,低于768字节的,不会进行overflowpage存储,某些情况下会减少结果集IO.
Barracuda (innodb-plugin)
ROW_FORMAT=DYNAMIC
这两者主要是功能上的区别功能上的。另外在行里的变长字段和Antelope的区别是只存20个字节,其它的overflowpage存储。
--
ROW_FORMAT=COMPRESSED
另外这两都需要开启innodb_file_per_table=1
innodb_file_format在配置文件中指定;
row_format则在创建数据表时指定。
# 在创建表的时候可以指定行格式。
CREATE TABLE tableName1
( id int PRIMARYKEY)
ROW_FORMAT = COMPRESSED
KEY_BLOCK_SIZE = 8;
# 查看表的行格式
show table status like 'tableName1';
AVL树用于存储索引数据
当我们用树的结构来存储索引的时候,访问一个节点就要跟磁盘之间发生一次IO。InnoDB操作磁盘的最小的单位是一页(或者叫一个磁盘块),大小是16K(16384字节)。
那么,一个树的节点就是16K的大小。
如果我们一个节点只存一个键值+数据+引用,例如整形的字段,可能只用了十几个或者几十个字节,它远远达不到16K的容量,所以访问一个树节点,进行一次IO的时候,浪费了大量的空间。
所以如果每个节点存储的数据太少,从索引中找到我们需要的数据,就要访问更多的节点,意味着跟磁盘交互次数就会过多。
如果是机械硬盘时代,每次从磁盘读取数据需要10ms左右的寻址时间,交互次数越多,消耗的时间就越多。
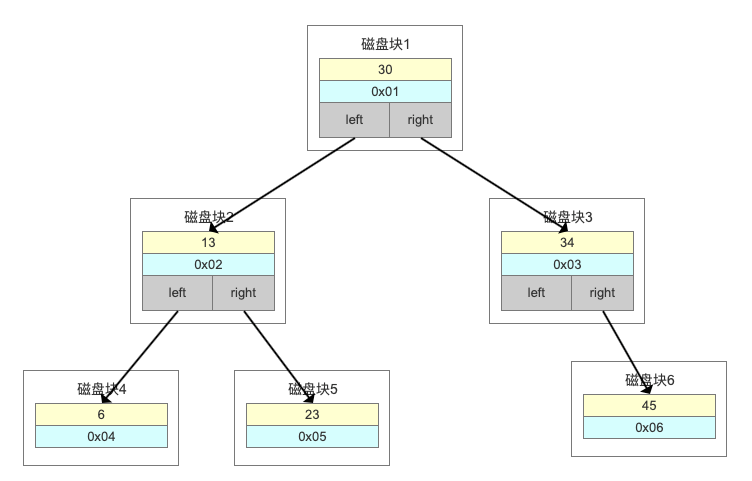
比如上面这张图,我们一张表里面有6条数据,当我们查询id=23的时候,要查询两个子节点,就需要跟磁盘交互3次,如果我们有几百万的数据呢?这个时间更加难以估计。
所以我们的解决方案是什么呢?
第一个就是让每个节点存储更多的数据。
第二个,节点上的关键字的数量越多,我们的指针数也越多,也就是意味着可以有更多的分叉(我们把它叫做“路数”)。
因为分叉数越多,树的深度就会减少(根节点是0)。
这样,我们的树是不是从原来的高瘦高瘦的样子,变成了矮胖矮胖的样子?
这个时候,我们的树就不再是二叉了,而是多叉,或者叫做多路。
4. 多路平衡查找树(BTree)(分裂、合并)
Balanced Tree这个就是我们的多路平衡查找树,叫做BTree(B代表平衡)。
跟AVL树一样,B树在枝节点和叶子节点存储键值、数据地址、节点引用。
它有一个特点:分叉数(路数)永远比关键字数多1。比如我们画的这棵树,每个节点存储两个关键字,那么就会有三个指针指向三个子节点。
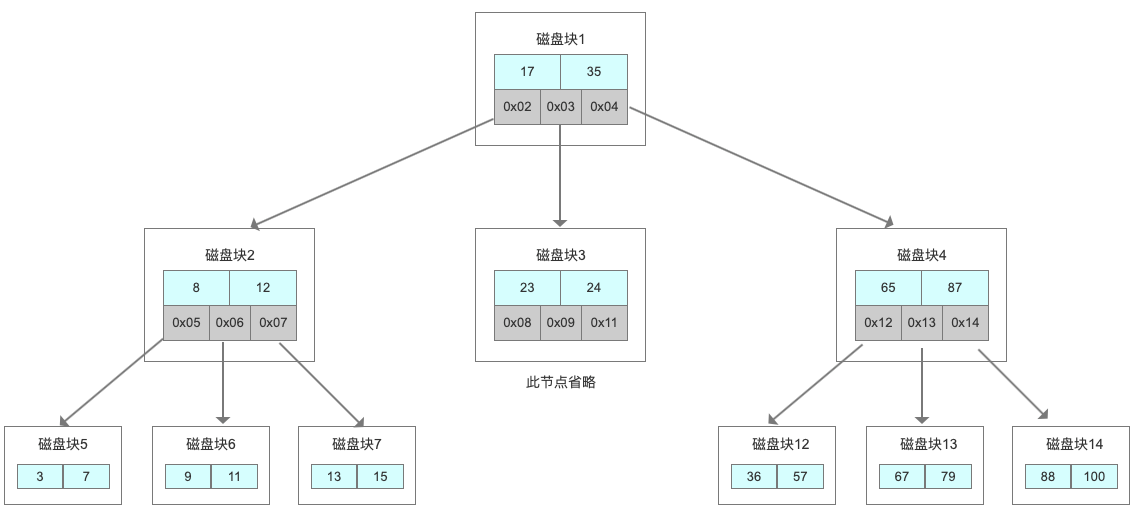
B Tree的查找规则是什么样的呢?
比如我们要在这张表里面查找15。
因为15小于17,走左边。
因为15大于12,走右边。
在磁盘块7里面就找到了15,只用了<3>次IO。
这个是不是比AVL树效率更高呢?那BTree又是怎么实现一个节点存储多个关键字,还保持平衡的呢?跟AVL树有什么区别?
https://www.cs.usfca.edu/~galles/visualization/BTree.html
比如MaxDegree(路数)是3的时候,我们插入数据1、2、3,在插入3的时候,本来应该在第一个磁盘块,但是如果一个节点有三个关键字的时候,意味着有4个指针,子节点会变成4路,所以这个时候必须进行分裂。把中间的数据2提上去,把1和3变成2的子节点。
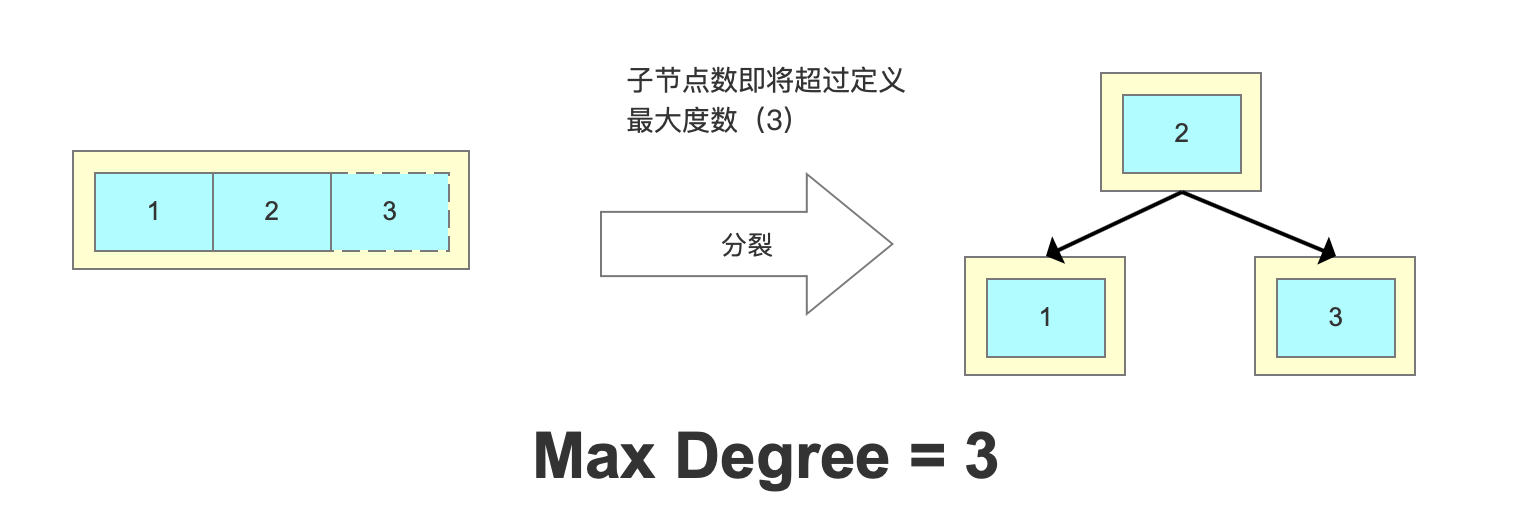
从这个里面我们也能看到,在更新索引的时候会有大量的索引的结构的调整,所以解释了为什么我们不要在频繁更新的列上建索引,或者为什么不要更新主键。
节点的分裂和合并,其实就是InnoDB页的分裂和合并。
5. B+树(加强版多路平衡查找树)
BTree的效率已经很高了,为什么MySQL还要对BTree进行改良,最终使用了B+Tree呢?
总体上来说,这个B树的改良版本解决的问题比BTree更全面。
我们来看一下InnoDB里面的B+树的存储结构:
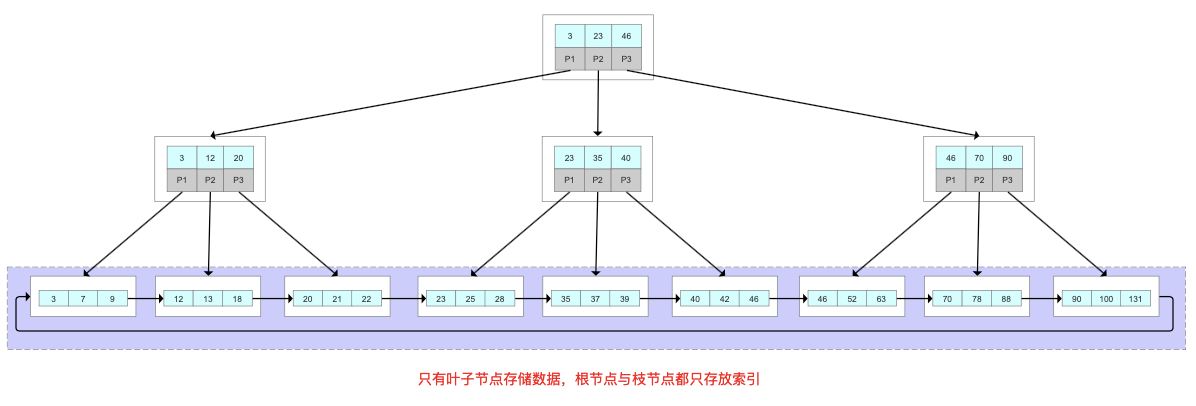
MySQL中的B+Tree有几个特点:
1、它的关键字的数量是跟路数相等的
2、B+Tree的根节点和枝节点中都不会存储数据,只有叶子节点才存储数据。搜索到关键字不会直接返回,会到最后一层的叶子节点。比如我们搜索id=28,虽然在第一层直接命中了,但是全部的数据在叶子节点上面,所以我还要继续往下搜索,一直到叶子节点。
举个例子:假设一条记录是1K,一个叶子节点(一页)可以存储16条记录。非叶子节点可以存储多少个指针?
假设索引字段是bigint类型,长度为8字节。指针大小在InnoDB源码中设置为6字节,这样一共14字节。非叶子节点(一页)可以存储16384/14=1170个这样的单元(键值+指针),代表有1170个指针。
树深度为2的时候,有1170^2个叶子节点,可以存储的数据为1170_1170_16=21902400。
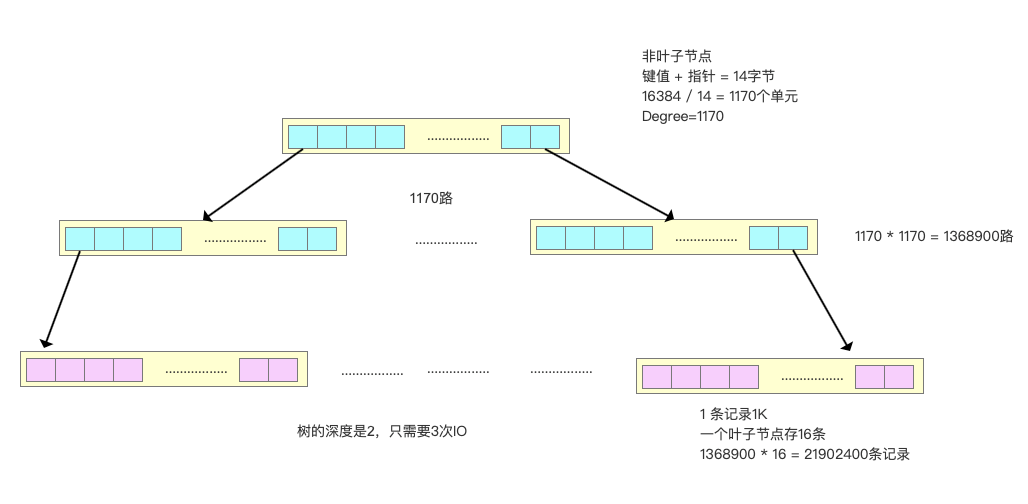
在查找数据时一次页的查找代表一次IO,也就是说,一张2000万左右的表,查询数据最多需要访问3次磁盘。
所以在InnoDB中B+树深度一般为1-3层,它就能满足千万级的数据存储。
3、B+Tree的每个叶子节点增加了一个指向相邻叶子节点的指针,它的最后一个数据会指向下一个叶子节点的第一个数据,形成了一个有序链表的结构。
4、它是根据左闭右开的区间[)来检索数据。
覆盖索引
InnoDB中,主键索引和辅助索引是有主次之分的。如果一个表有主键索引,那么主键索引就是聚集索引。其他索引统一叫“二级索引”。
二级索引存储的是二级的键值,如在name建立索引,节点上存的就是name的值。
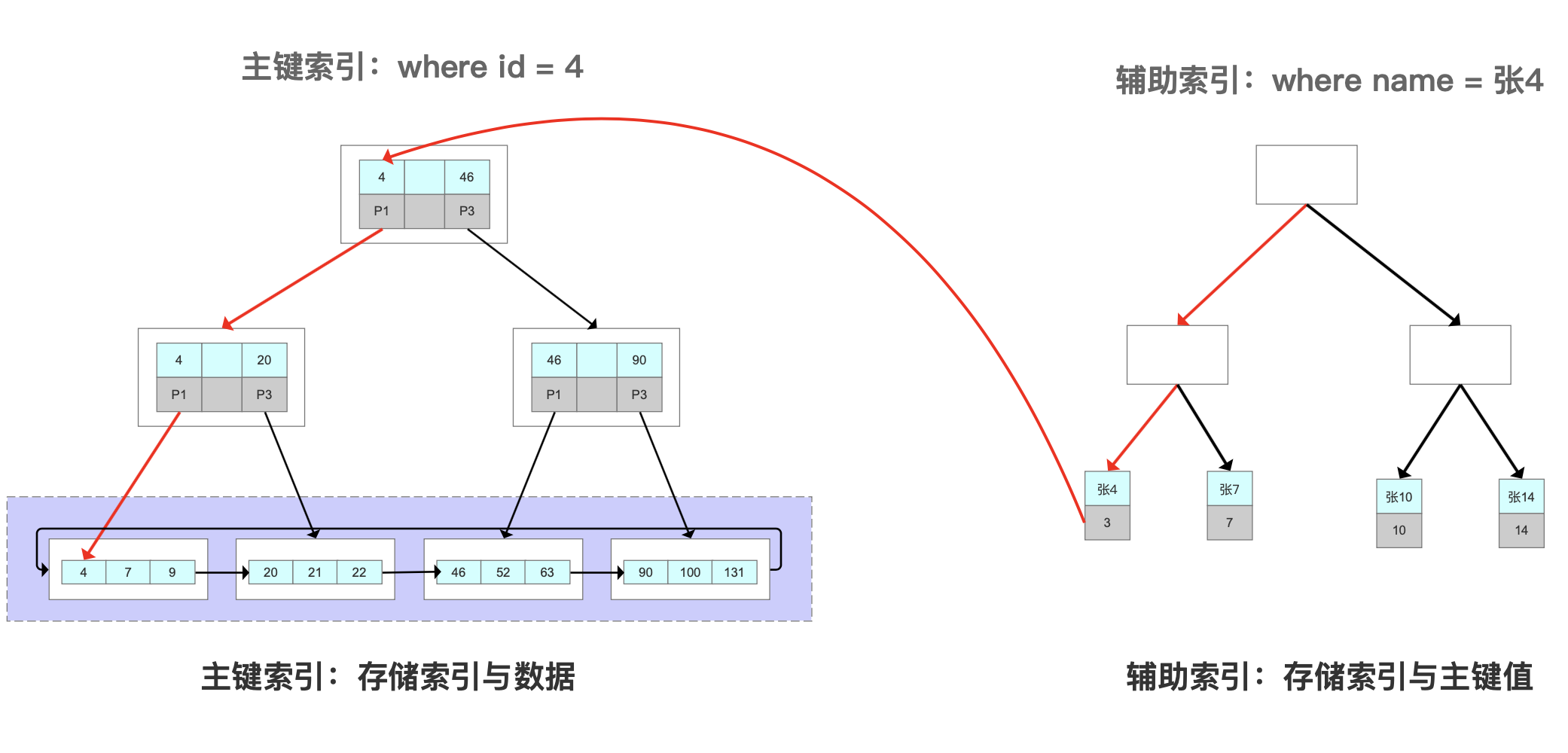
二级索引检索数据的流程是:
当使用name索引查询一条记录,它会在二级索引的叶子节点找到name=张4,并拿到主键值如id = 1,然后再到主键索引的叶子节点拿到数据。
为什么不存地址而存键值? 因为地址会变化
索引的创建
1、在用于where判断order排序和join的(on)字段上创建索引
2、索引的个数不要过多。——浪费空间,更新变慢。
3、区分度低的字段,例如性别,不要建索引。——离散度太低,导致扫描行数过多。
4、频繁更新的值,不要作为主键或者索引。——页分裂
5、组合索引把散列性高(区分度高)的值放在前面。
6、创建复合索引,而不是修改单列索引。