目录
- 课堂内容总结
- 课后教材测试
课堂内容总结
一、信息的表示与处理
信息=位+上下文
- 算术方面:加法器(解决 + 、- 、× 、÷ 等)
- 逻辑方面:与非门(解决 & 、| 、~ 、^ 等)
二、进制转换
使用堆栈(整数部分逆序输出,小数部分正序输出)
- C语言中使用堆栈法实现各进制(十进制、二进制、八进制、十六进制)之间的转换
三、位的表示
移位,置0,置1……
- 位运算:&(按位与)、|(按位或)、~(非)、^(按位异或)
- 使用位向量
- 逻辑运算:&&(逻辑与)、||(逻辑或)、!(逻辑非)
- 结果只有0或1
- 移位运算:逻辑移位、算术移位
- 考点:取某些特定位(进行移位)
四、数值与编码规则
信息=位+上下文
- 无符号整数
- B2U,U2B
- 有符号整数
- B2T,T2B
- 采用补码编码(不采用原码/反码原因:不唯一、不正确)
- 浮点数
- C语言中不对浮点数进行比较,因为可能会出现不等或无法表达的错误结果
- 统一采用IEEE浮点表示
五、数值运算
- 无符号数运算
- 溢出:x+y(mod2^w)
- 乘法也一致
- 有符号数运算
- 补码运算
- -2^w≤x+y≤2^(w-2)
- 补码运算中,正数不变,负数取反加一
- 乘法也一致
六、信息的存储
- 大端和小端
- 小端:高(字节)对高(地址),低(字节)对低(地址)
- 大端:高(字节)对低(地址),低(字节)对高(地址)
- 网络字节序
- 一般都是大端模式的字节序,因此不用再转换
- 若为网络小端上传至主机,则需要先转化为大端再上传
- 转化方法:移位(左移<<,右移>>)
- 主机字节序
返回目录
课后教材测试
教材《深入理解计算机系统》
一、教材p97 2.96
1. 题目
遵循位级浮点编码规则,实现具有如下原型的函数:
/*
*Compute (int) f.
* If conversion causes overflow or f is NaN, return 0x80000000
* int float_f2i(float bits f);
*/
对于浮点数f,这个函数计算(int)f。如果f是NaN,你的函数应该向零舍人。如果f不能用整数表示(例如,超出表示范围,或者它是一个NaN),那么函数应该返回0x80000000。
测试你的函数,对参数f可以取的所有2^32个值求值,将结果与你使用机器的浮点运算得到的结果相比较。
2. 分析
位级浮点编码规则是什么?
- 代码要实现浮点函数在浮点数的位级表示上直接运算;
- 代码完全遵循IEEE浮点运算规则,使用偶数舍入;
- 代码的数据类型是 float_bits ,而非 float;
- 可以使用数据类型 int 和 unsigned ,包括无符号和整数常数和运算;
- 不可使用任何联合、结构和数组;更不可使用浮点数据类型、运算或常数;
- 对于参数 f ,若 f 是非规格化的,该函数返回 ±0(保持 f 的符号),否则返回 f。
f 是 NaN是什么意思?
NaN,是Not a Number的缩写,在IEEE浮点数算术标准(IEEE 754)中定义,表示一些特殊数值(无穷与非数值(NaN)),为许多CPU与浮点运算器所采用。
NaN是无序的,无法对其进行逻辑运算。它不大于、小于或等于任何数(包括它自己),将<,>,<=,和>=作用于NaN产生一个exception。得到NaN时就查看是否有非法操作,如果表达式中含有NaN,那么表达式的结果为NaN。
下面是NaN的产生原因:

f 是 NaN 即表示 f 是‘“无效数字”。
判断
f 是 NaN的方法?
//判断一个浮点数是否是NaN
int IsNaN(float x)
{
return !(x==x);
}
//将判断NaN的宏定义在<math.h>头文件中
#include <math.h>
int IsNaN(x) //当x时nan返回1,其它返回0
3. 代码
#include <stdio.h>
typedef unsigned float_bits;
float_bits float_f2i(float_bits f);
float u2f(unsigned x);
int main()
{
unsigned i = 0x00000001;
printf("%d\t%d\n", (int)u2f(i), float_f2i(i));
i = 0x43800000;
printf("%d\t%d\n", (int)u2f(i), float_f2i(i));
i = 0x4E800000;
printf("%d\t%d\n", (int)u2f(i), float_f2i(i));
i = 0xFFFFFFFF;
printf("%d\t%d\n", (int)u2f(i), float_f2i(i));
return 0;
}
float_bits float_f2i(float_bits f)
{
unsigned sign = f >> 31;
unsigned exp = f >> 23 & 0xFF;
unsigned frac = f & 0x7FFFFF;
unsigned bias = 127;
unsigned num;
unsigned E, M;
if (exp >= 0 && exp < 0 + bias)
num = 0;
else if (exp >= 31 + bias)
num = 0x80000000;
else {
E = exp - bias;
M = frac | 0x800000;
if (E > 23)
num = M << (E -23);
else
num = M >> (23 - E);
}
return sign ? -num : num;
}
float u2f(unsigned x)
{
return *(float *)&x;
}
4. 截图
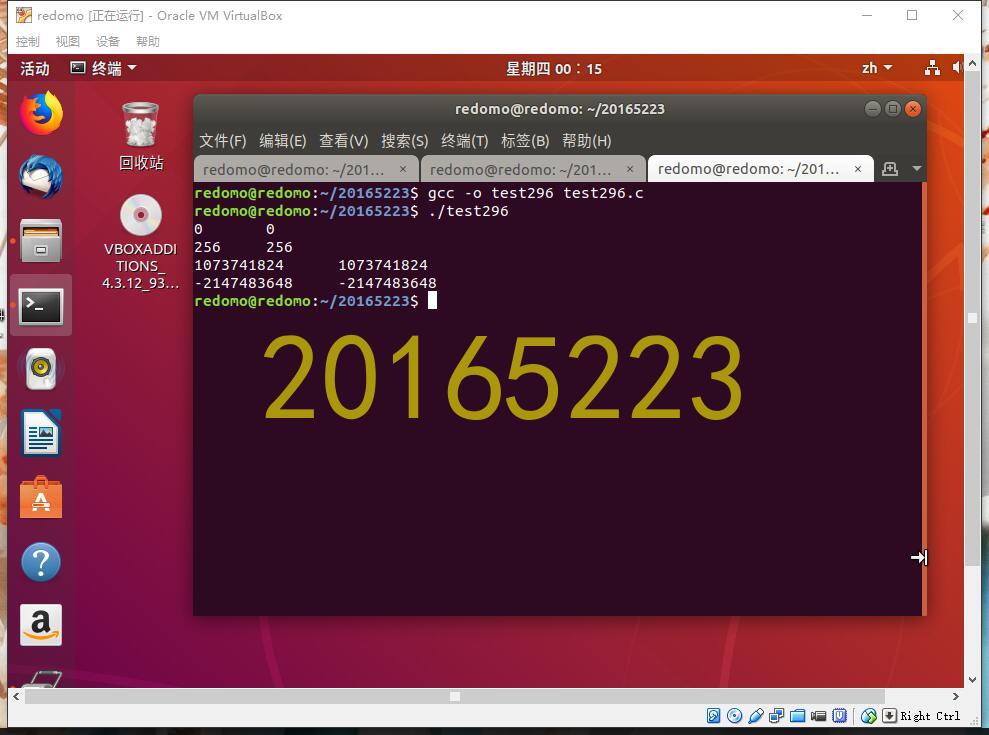
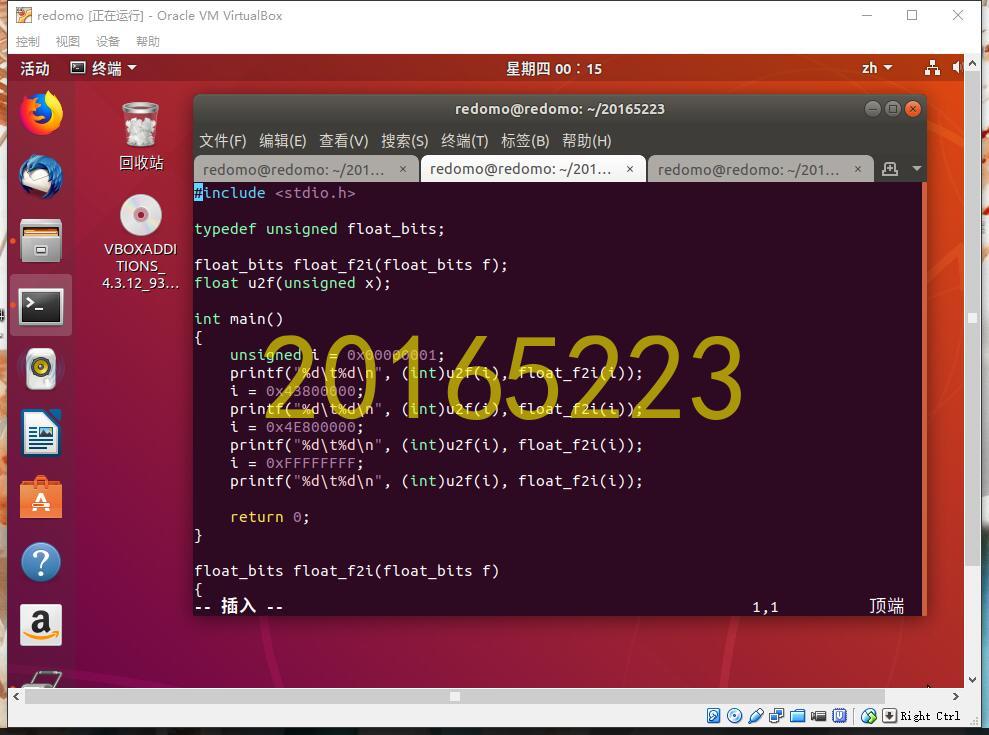
二、教材p97 2.97
1. 题目
遵循位级浮点编码规则,实现具有如下原型的函数:
/* Compute (float) i */
float_bits float_i2f(int i);
对于函数i,这个函数计算(float) i的位级表示。
测试你的函数,对参数f可以取的所有2^32个值求值,将结果与你使用机器的浮点运算得到的结果相比较。
2. 代码
#include <stdio.h>
#include <limits.h>
typedef unsigned float_bits;
float_bits float_i2f(int i);
unsigned bits_length(int x);
unsigned bits_mask(unsigned x);
float u2f(unsigned x);
int main()
{
int i = 123;
printf("%f\t%f\n", (float)i, u2f(float_i2f(i)));
i = -123;
printf("%f\t%f\n", (float)i, u2f(float_i2f(i)));
i = 0;
printf("%f\t%f\n", (float)i, u2f(float_i2f(i)));
i = (~0);
printf("%f\t%f\n", (float)i, u2f(float_i2f(i)));
i = (1 << 31);
printf("%f\t%f\n", (float)i, u2f(float_i2f(i)));
return 0;
}
float_bits float_i2f(int i)
{
unsigned sign, exp, frac, bias;
bias = 127;
if (i == 0)
return 0;
if (i == INT_MIN) { // -1
sign = 1;
exp = 31 + bias;
frac = 0; // -1是整数,没有小数部分
return sign << 31 | exp << 23 | frac;
}
sign = i > 0 ? 0 : 1;
if (i < 0)
i = -i;
unsigned bits_num = bits_length(i);
unsigned fbits_num = bits_num - 1;
unsigned fbits;
exp = bias + fbits_num;
fbits = i & bits_mask(1 << fbits_num - 1);
if (fbits_num <= 23)
frac = fbits << (23 - fbits_num);
else {
unsigned offset = fbits_num - 23;
frac = fbits >> offset;
unsigned round_mid = 1 << (offset - 1);
unsigned round_part = fbits & bits_mask(1 << offset - 1);
if (round_part > round_mid)
++frac;
else if (round_part == round_mid) {
if (frac & 0x1)
++frac;
}
}
return sign << 31 | exp << 23 | frac;
}
unsigned bits_length(int x)
{
unsigned ux = (unsigned) x;
unsigned count = 0;
while (ux > 0) {
ux >>= 1;
++count;
}
return count;
}
unsigned bits_mask(unsigned x)
{
x |= x >> 1;
x |= x >> 2;
x |= x >> 4;
x |= x >> 8;
x |= x >> 16;
return x;
}
float u2f(unsigned x)
{
return *(float *)&x;
}
3. 截图
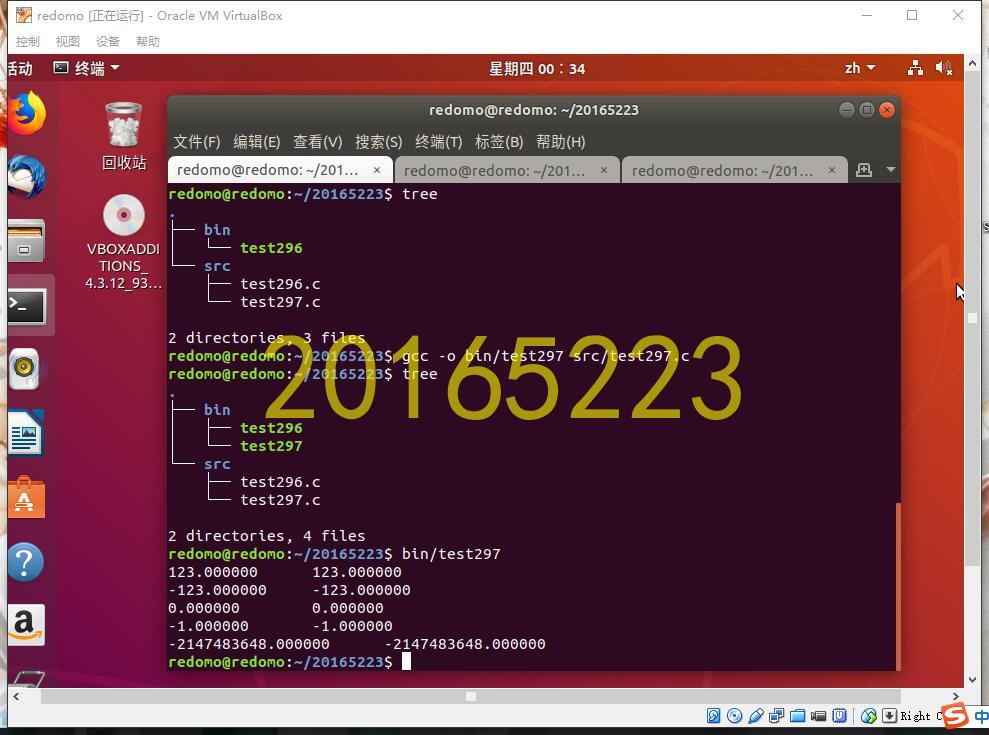
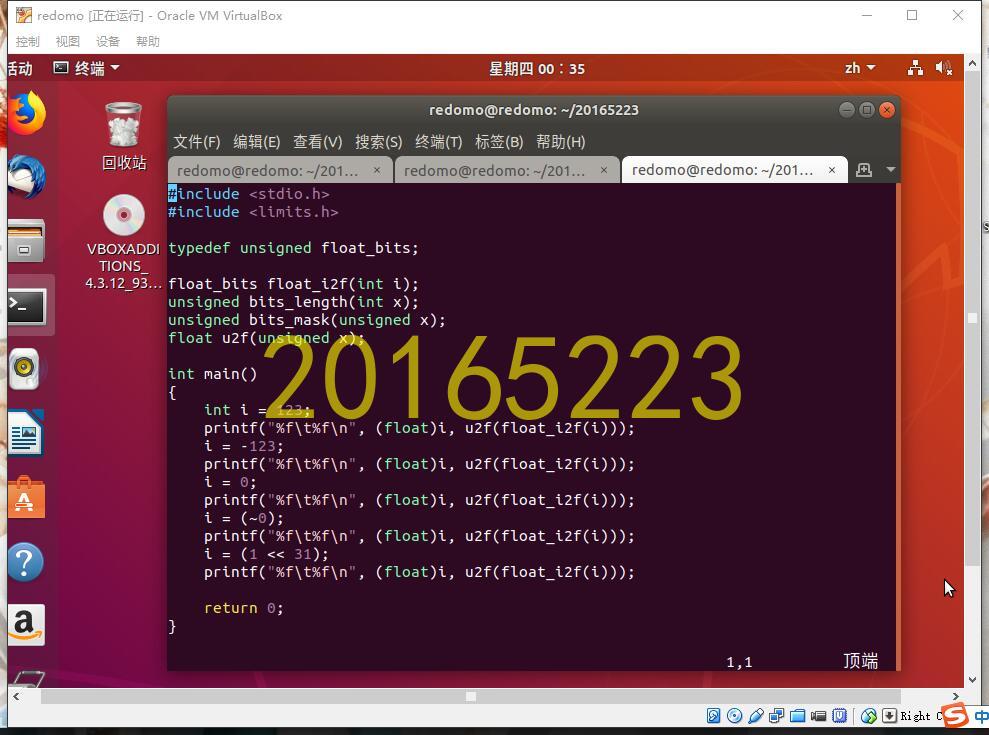
返回目录













