最小生成树之普利姆( Prim )算法
如果想看克鲁斯卡尔算法(Kruskal),请移步
--------->这是链接🔗{{>_<}}<-----------
- 例子
- 图示
- 代码
我们来讲述普利姆( Prim )算法。
和克鲁斯卡尔算法一样,普利姆算法也是一种构造最小生成树的算法。
- 主要思想是:
首先随意从一个点出发,然后每次找他们的最小相邻边,每经过一个顶点,那边找其顶点的最小权值的边。一直到找到了 n 条边,( n=定点数-1 ) 然后我们的算法结束
普利姆算法是利用了贪心思想的特性,但是对于有负权值的边,普利姆算法并不适用,此时应该用克鲁斯卡尔算法 ( ------>这是我的另一篇文章,讲述克鲁斯卡尔算法,有兴趣看看啊♪(´▽`)<------ )
举个栗子 (╹ڡ╹ ) :比如有六个城市,分别是城市1,城市2,城市3,城市4,城市5,城市6,我们的目标是:选择几条线路,把这几个城市连起来,让城市间能够相互到达,但是不能有回路。如图.....
在这几个城市中,我们测量了每个城市之间的路线,他们的权值分别如下:
开始城市
到达城市
路线长度(权值)
城市1
城市2
1
城市1
城市3
12
城市1
城市4
2
城市1
城市5
5
城市2
城市6
4
城市2
城市4
12
城市6
城市5
4
城市5
城市4
5
城市4
城市3
20
也就是如图所示:
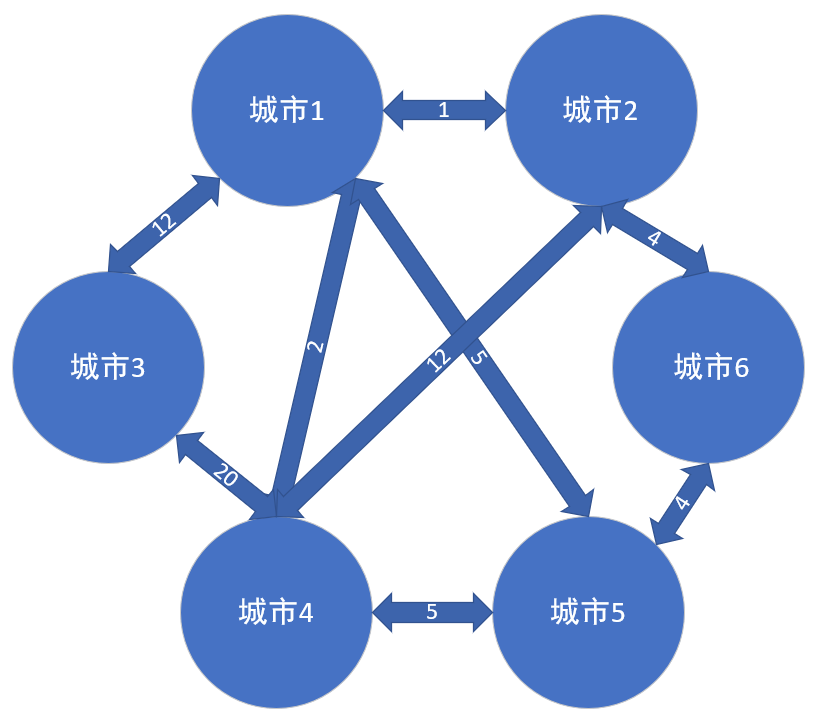
然后,我们的目标是,从这几条边中找到能够连通所有点的边并且这些边是最小权值的。也就是像下面的图一样
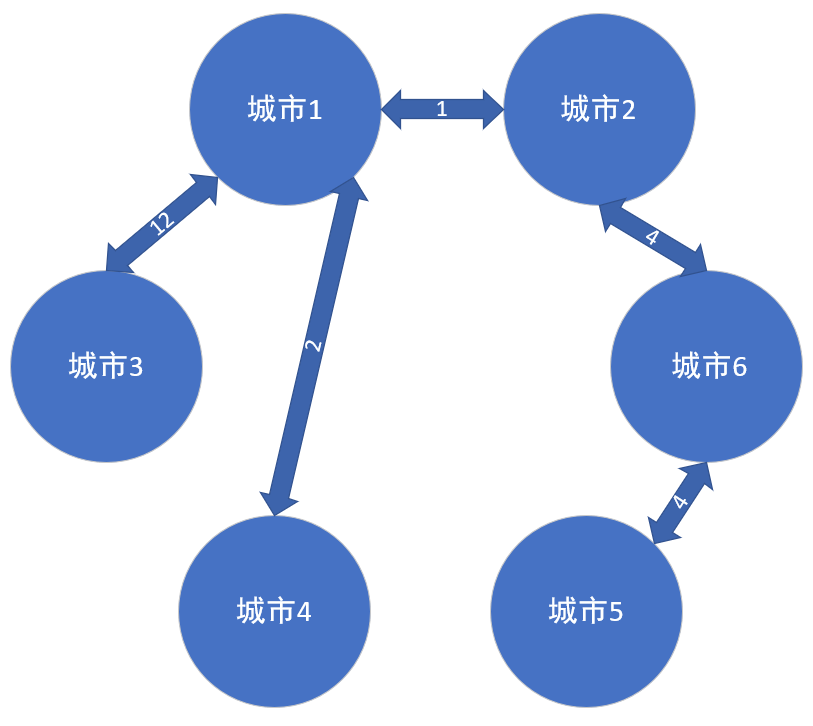
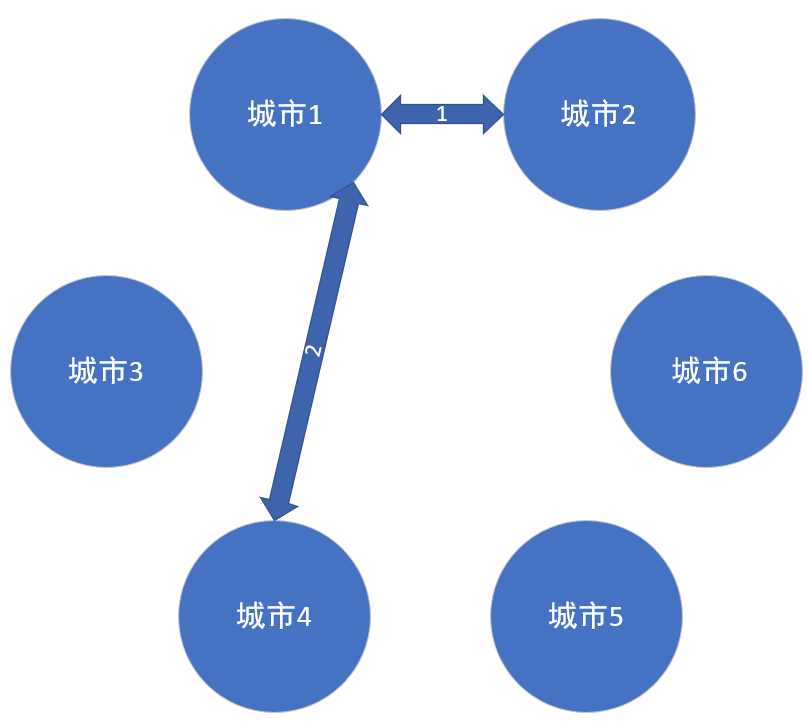
然后我们,从城市1开始吧 o( *  ̄ ▽  ̄ * )o。
从城市1开始的话,我们会把城市1所相邻的边放进一个集合里面,然后找城市1相邻的边的最小值。我们很容易可以找到,它是1,那么我们把1选上,然后1所相连的是城市2,这样,我们找到了第一条路径,并且这条路径是能够从城市1到达城市2的 (o゜▽゜)o☆
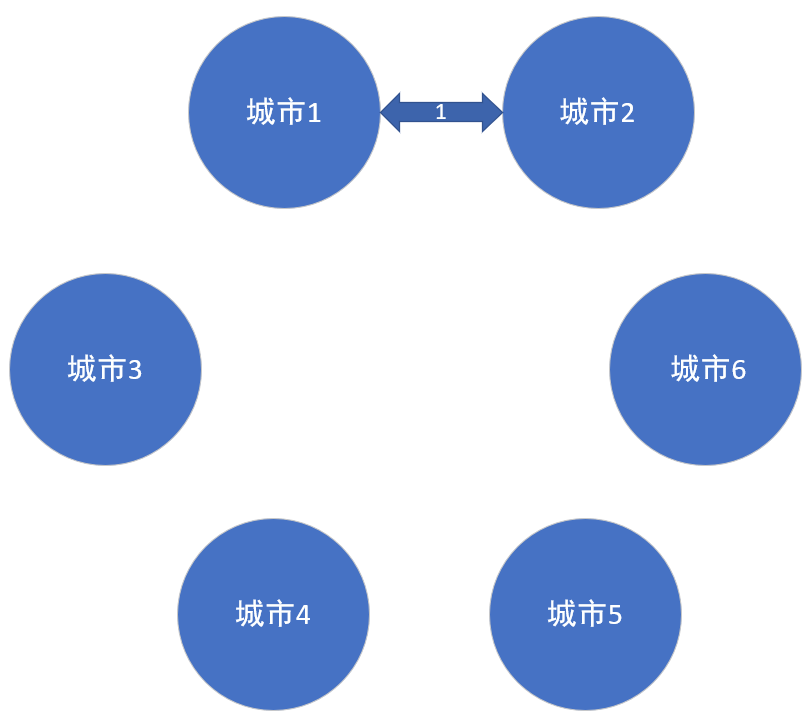
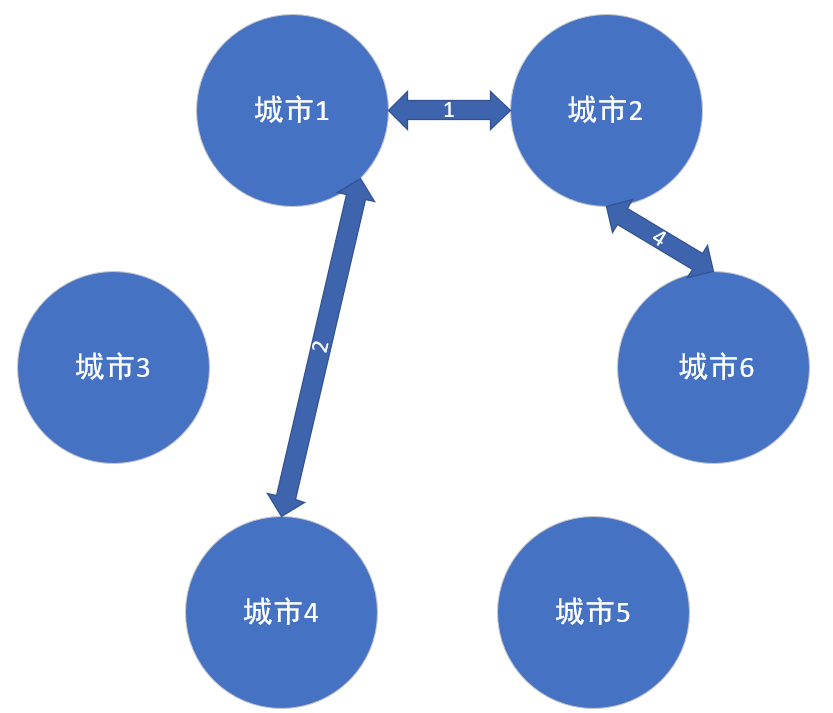
从城市1开始,我们把边1,2,5,12放进集合了,然后我们选了1,现在把1从集合里面移除。由于加入了城市2,那么我们把城市2相关邻的边放进集合里面,此时集合里面就有了2,5,12,4,12,然后我们再在这里面找权值最小的边,然后再相连,然后重复这个操作。
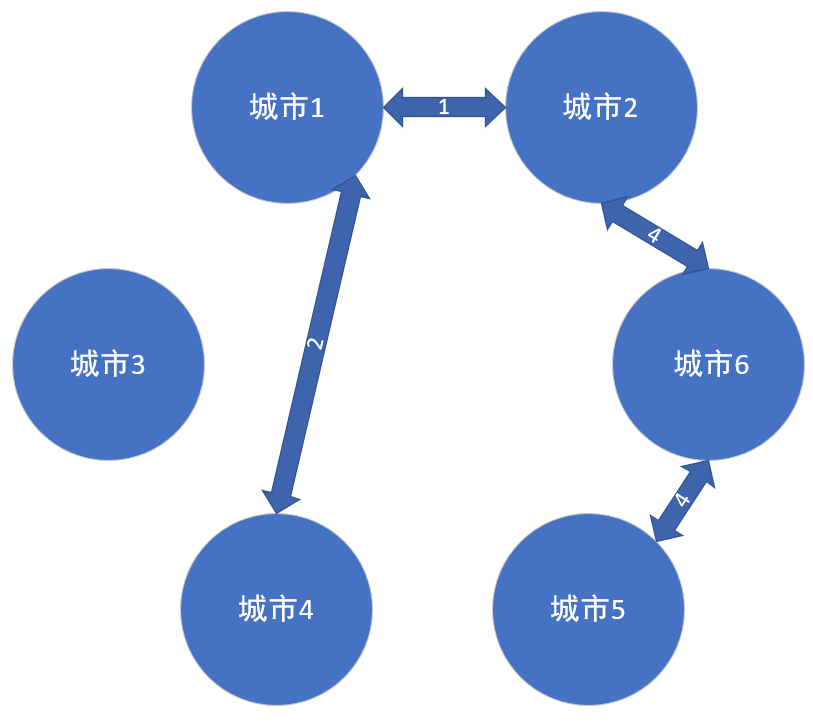
当你找到一条边,这条边刚刚好两边都经历过了,那我们就舍弃这条边,然后继续向下找,直到所有的点都遍历过了之后,就结束操作,我们就构成了一棵最小生成树。
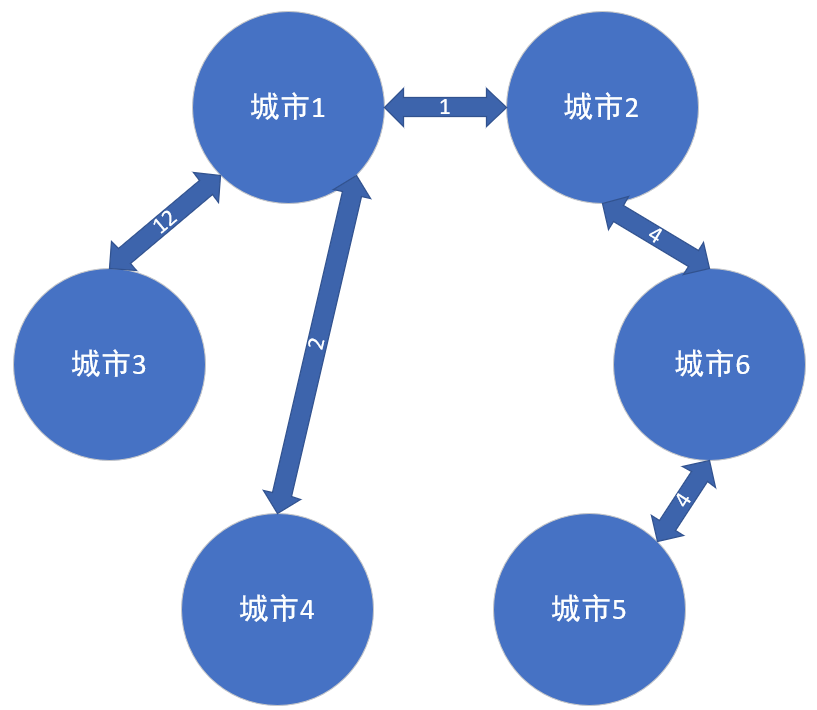
- \[返回\](#back)
然后让我们来看看代码的实现。代码实现,我采用了邻接矩阵的存储结构
main.cpp
#include"GraphPrim.h"
int main()
{
GraphPrim g1;
g1.Init();
g1.Display();
return 0;
}
GraphPrim.h
#pragma once
#ifndef _GRAPHPRIM_H_
#define _GRAPHPRIM_H_
#include<iostream>
#include<cstdlib>
#include<vector>
using namespace std;
const int MAX = INT_MAX;
class GraphPrim
{
private:
vector<vector<int>>graph;//邻接矩阵存储点与边的关系
vector<bool>visited;//判断是否经历过
vector<int>side;
vector<int>node;//取点的路径,用来存放输出点的顺序
vector<int>useSide;//使用的边,用来存放边的权值
int nodeNumber;//点的个数
int startPoint;//开始点
int sum;
int findMin(vector<int>& ans);//返回下标
public:
void Init();//初始化
void Prim(int start);//普利姆算法,以及开始点
void Display();//显示参数
};
#endif // !_GRAPHPRIM_H_
Graphprim.cpp
#include "GraphPrim.h"
int GraphPrim::findMin(vector<int>& ans)
{
int index = 0;
int min = ans[0];
for (int i = 0; i < ans.size(); i++)
{
if (min > ans[i])
{
min = ans[i];
index = i;
}
}
return index;
}
void GraphPrim::Init()
{
cout << "请输入点的个数" << endl;
cin >> nodeNumber;
visited.resize(nodeNumber + 1);//初始化
graph.resize(nodeNumber + 1);//初始化
for (int i = 0; i <nodeNumber + 1; i++)
graph[i].resize(nodeNumber + 1, MAX);
cout << "请输入开始点" << endl;
cin >> startPoint;
int a, b;
cout << "请输入出发点、到达点和路径长度,以‘#’为全部结束" << endl;
while ((cin >> a && a != '#') && (cin >> b && b != '#'))
{
cin >> graph[a][b];//输入权值
graph[b][a] = graph[a][b];
}
}
void GraphPrim::Prim(int start)
{
int temp;
sum = 0;
side.resize(nodeNumber + 1);
node.push_back(start);
visited[start] = true;
for(int i = 1; i <= nodeNumber; i++)
side[i] = graph[start][i];
for(int i = 1; i <= nodeNumber; i++)//找生成树集合点集相连最小权值的边
{
temp = MAX;
for(int j = 1; j <= nodeNumber; j++)
if (!visited[j] && temp > side[j])
{
temp = side[start = j];
}
if(temp == MAX)//如果是无穷了
break;
visited[start] = true; //加入最小生成树集合
node.push_back(start);
useSide.push_back(temp);
sum += temp;//记录权值之和
for(int j = 1; j <= nodeNumber; ++j) //更新边数组
if (!visited[j] && side[j] > graph[start][j])
{
side[j] = graph[start][j];
}
}
}
void GraphPrim::Display()
{
Prim(startPoint);
cout << "显示最大权值" << sum << endl;
cout << "路径显示: ";
for (int i = 0; i < node.size(); i++)
cout << node[i] << " ";
cout << endl;
}
- 返回













