总结
优先队列的作用是能保证每次取出的元素都是队列中权值最小的(Java的优先队列每次取最小元素,C++的优先队列每次取最大元素)。这里牵涉到了大小关系,元素大小的评判可以通过元素本身的自然顺序(_natural ordering_),也可以通过构造时传入的比较器(_Comparator_,类似于C++的仿函数)。
Java中PriorityQueue实现了_Queue_接口,不允许放入
null元素;其通过堆实现,具体说是通过完全二叉树(_complete binary tree_)实现的小顶堆(任意一个非叶子节点的权值,都不大于其左右子节点的权值)。Java中使用数组的形式保存小顶堆的结构。父节点和子节点的编号是有联系的,更确切的说父子节点的编号之间有如下关系:
leftNo = parentNo*2+1
rightNo = parentNo*2+2
parentNo = (nodeNo-1)/2
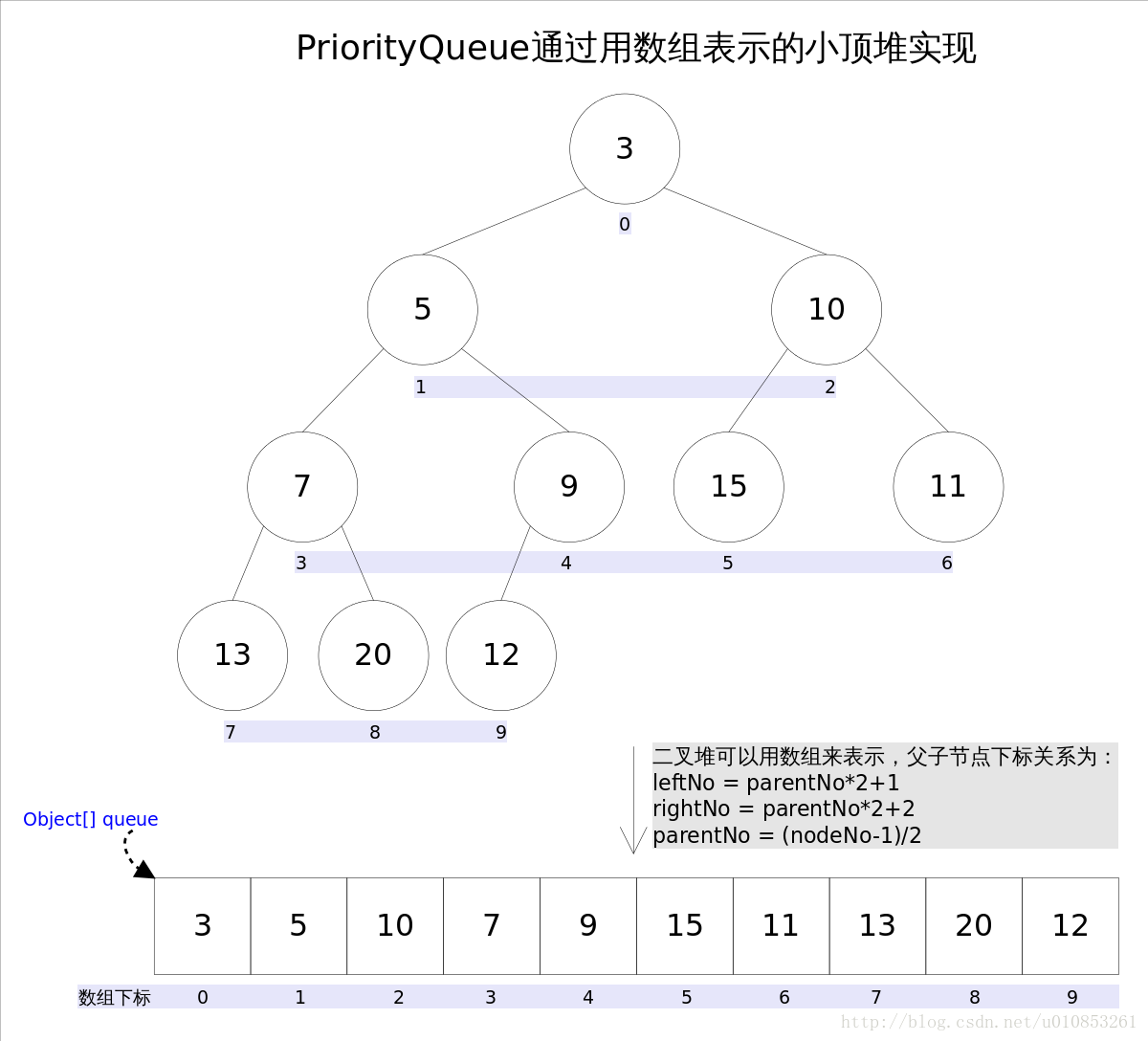
PriorityQueue解析
详细内容
- PriorityQueue 继承关系
- add() & offer() 源码 -- add(E e)和offer(E e)的语义相同,都是向优先队列中插入元素,只是Queue接口规定二者对插入失败时的处理不同,前者在插入失败时抛出异常,后则则会返回false。对于PriorityQueue这两个方法其实没什么差别。
- peek() 源码
- remove() & poll() 源码 -- remove()和poll()方法的语义也完全相同,都是获取并删除队首元素,区别是当方法失败时前者抛出异常,后者返回null。由于删除操作会改变队列的结构,为维护小顶堆的性质,需要进行必要的调整。
参考链接
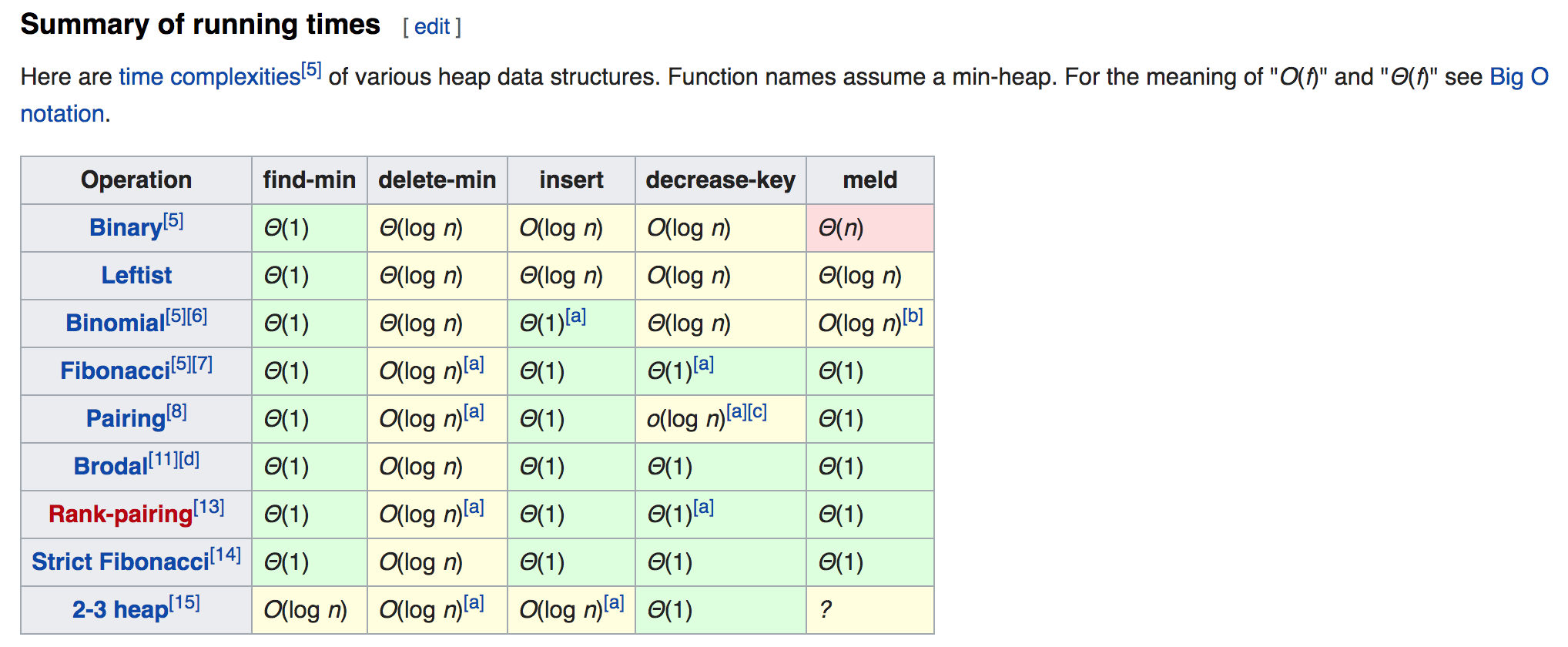
PriorityQueue 时间复杂度
- Binary heap (二叉树堆), Java默认使用, 也就是第一行。
- Fibonacci heap (斐波那契堆),Strict Fibonacci(严格斐波那契堆)理论性能最好 --> 记住大体概念,结论即可。
- Binomial heap(二项堆)
Fibonacci heap (斐波那契堆)的优缺点
Fibonacci heap (斐波那契堆)的优点:
斐波那契堆的结构较二项堆更松散。因此对结构的维护可以到方便时再做。
- 1.二叉堆及二项堆在插入一个结点后,会马上维护堆的结构...而FIB堆却将这个工作延迟到FIB_EXTRACT_MIN的时候再做**....使元素的插入的时间为**O(1)
- 2.二叉堆及二项堆在改变一个结点的值的时候,会马上维护堆的结构...而FIB堆却将这个工作延迟到FIB_EXTRACT_MIN的时候再做**....使元素的值的改变的时间为**O(1)
- 3.堆的合并..FIB堆只需要将两个堆的根表合并就可以了 O(1)
Fibonacci heap (斐波那契堆)的难点:
FIB_EXTRACT_MIN()...提取最小的值。
- 1.将****min结点的儿子都加入到根表
- 2.在根表中除去****min结点
- 3.合并堆的根表,即减少根表中堆的数目,直到根表中每个根的度都不相同(用**merge()函数)**











