F题

dsu on tree维护一个数组t[][][]。t[i][j][k]表示当前子树内a[u]=i且u的第j位是k的u的个数。

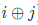这个东西没办法直接维护的，但是对于，你没必要知道是什么，假如的第位是0，那么你需要知道第位是1的的个数即可。

因此把直接拆成20位，就可以统计答案了。

我个人理解dsu on tree对于处理子树间的贡献和子树内的贡献这两种不同的题型有两种不同的写法，需要特别注意。

#include<bits/stdc++.h>
#define pb push_back
#define fi first
#define se second
#define sz(x)  (int)x.size()
#define cl(x)  x.clear()
#define all(x)  x.begin() , x.end()
#define rep(i , x , n)  for(int i = x ; i <= n ; i ++)
#define per(i , n , x)  for(int i = n ; i >= x ; i --)
#define mem0(x)  memset(x , 0 , sizeof(x))
#define mem_1(x)  memset(x , -1 , sizeof(x))
#define mem_inf(x)  memset(x , 0x3f , sizeof(x))
#define debug(x)  cerr << #x << " = " << x << '\n'
#define ddebug(x , y)  cerr << #x << " = " << x << "   " << #y << " = " << y << '\n'
#define ios std::ios::sync_with_stdio(false) , cin.tie(0)
using namespace std ;
typedef long long ll ;
typedef long double ld ;
typedef pair<int , int> pii ;
typedef pair<ll , ll> pll ;
typedef double db ;
const int mod = 998244353 ;
const int maxn = 1e5 + 10 ;
const int maxm = 1e6 + 1e5 + 10 ;
const int inf = 0x3f3f3f3f ;
const double eps = 1e-6 ; 
int n , a[maxn] ;
int c[maxn] ;
vector<int> g[maxn] ;
ll ans = 0 ;
struct Dsu_on_tree
{
    int siz[maxn] , son[maxn] ;
    int flag ;
    int t[maxm][20][2] ; //t[i][j][k]表示a[u]=i且u的第j位是k的u的个数
    void init() 
    {
        flag = 0 ;
        memset(siz , 0 , sizeof(siz)) ;
        memset(son , 0 , sizeof(son)) ;
        memset(t , 0 , sizeof(t)) ;   
        rep(i , 0 , 19)  c[i] = (1 << i) ;
    }
    void dfs1(int f , int u)
    {
        siz[u] = 1 ;
        for(auto v : g[u])
        {
            if(v == f) continue ;
            dfs1(u , v) ; 
            siz[u] += siz[v] ;
            if(siz[v] > siz[son[u]]) son[u] = v ;
        }
    }
    void add(int u , int x)
    {
        int tmp = a[u] ;
        rep(j , 0 , 19)  t[tmp][j][u % 2] += x , u /= 2 ;
    }
    void dfs3(int fa , int u , int lca)
    {
        int s = (a[u] ^ a[lca]) ;
        int tmp = u ;
        rep(j , 0 , 19)  ans += 1ll * t[s][j][1 - (tmp % 2)] * c[j] , tmp /= 2 ;
        for(auto v : g[u])
        {
            if(v == fa)  continue ;
            dfs3(u , v , lca) ;
        }
    }
    void dfs4(int fa , int u , int x)
    {
        add(u , x) ;
        for(auto v : g[u])
        {
            if(v == fa)  continue ;
            dfs4(u , v , x) ;
        }
    }
    void calc(int f , int u , int x)
    {
        for(auto v : g[u])
        {
            if(v == f || v == flag) continue ;
            if(x == 1)  dfs3(u , v , u) ;
            dfs4(u , v , x) ;
        }
        add(u , x) ;
    }
    void dfs2(int f , int u , int keep)
    {
        for(auto v : g[u])
        {
            if(v == f || v == son[u]) continue ;
            dfs2(u , v , 0) ;
        }
        if(son[u])  dfs2(u , son[u] , 1) , flag = son[u] ;
        calc(f , u , 1) ;
        if(son[u]) flag = 0 ;
        if(!keep)  calc(f , u , -1) ;
    }
} dsu_on_tree ;
int main()
{
    ios ;
    cin >> n ;
    rep(i , 1 , n)  cin >> a[i] ;
    rep(i , 1 , n - 1)
    {
        int u , v ;
        cin >> u >> v ;
        g[u].pb(v) , g[v].pb(u) ;
    }
    dsu_on_tree.init() ;
    dsu_on_tree.dfs1(1 , 1) ;
    dsu_on_tree.dfs2(1 , 1 , 0) ;
    cout << ans << '\n' ;
    return 0 ;
}

K题

不妨设，打表后会发现，这就可以直接预处理出符合条件的二元组了。

但是还是不好直接做，不过如果打表技术再高超一点，会发现对于每个，满足条件的最多只有个。

这样操作2就按秩合并，操作3就暴力修改。

PS：其实F题需要想到拆位，K题需要想到满足条件的二元组不是很多，才可以做。假如都想到了，那么K比F好写很多。不过如果都没想到，那这场就没了。

#include<bits/stdc++.h>
#define pb push_back
#define fi first
#define se second
#define sz(x)  (int)x.size()
#define cl(x)  x.clear()
#define all(x)  x.begin() , x.end()
#define rep(i , x , n)  for(int i = x ; i <= n ; i ++)
#define per(i , n , x)  for(int i = n ; i >= x ; i --)
#define mem0(x)  memset(x , 0 , sizeof(x))
#define mem_1(x)  memset(x , -1 , sizeof(x))
#define mem_inf(x)  memset(x , 0x3f , sizeof(x))
#define debug(x)  cerr << #x << " = " << x << '\n'
#define ddebug(x , y)  cerr << #x << " = " << x << "   " << #y << " = " << y << '\n'
#define ios std::ios::sync_with_stdio(false) , cin.tie(0)
using namespace std ;
typedef long long ll ;
typedef long double ld ;
typedef pair<int , int> pii ;
typedef pair<ll , ll> pll ;
typedef double db ;
const int mod = 998244353 ;
const int maxn = 3e5 + 10 ;
const int inf = 0x3f3f3f3f ;
const double eps = 1e-6 ; 
int n , q , a[maxn] ;
vector<int> v[maxn] ;
set<pii> s[maxn] ;
ll ans = 0 ;
struct Dsu
{
    int pre[maxn] , siz[maxn] ;
    void init(int n)
    {
        for(int i = 1 ; i <= n ; i ++)  pre[i] = i , siz[i] = 1 ;
    }
    int find(int u) 
    {
        if(pre[u] == u)  return u ;
        return pre[u] = find(pre[u]) ;
    }
    void join(int x , int y)
    {
        int fx = find(x) ;
        int fy = find(y) ;
        if(fx != fy)  
        {
            if(siz[fx] <= siz[fy])  pre[fx] = fy , siz[fy] += siz[fx] ;
            else  pre[fy] = fx , siz[fx] += siz[fy] ;
        }       
    }
    ll cal(int fx , int t , int cnt)
    {
        ll res = 0 ;
        for(auto u : v[t])
        {
            auto it = s[fx].lower_bound({u , 0}) ;
            if(it != s[fx].end())
            {
                int tt = (*it).fi ;
                int num = (*it).se ;
                if(tt == u)  res += 1ll * num * cnt ;
            }
        }
        return res ;
    }
    void merge(int x , int y)
    {
        int fx = find(x) ;
        int fy = find(y) ;
        if(fx != fy)  
        {
            if(siz[fx] < siz[fy])  swap(fx , fy) ;
            pre[fy] = fx ;
            siz[fx] += siz[fy] ;
            for(auto u : s[fy])
            {
                int t = u.fi ;
                int cnt = u.se ;
                ans += cal(fx , t , cnt) ;
            }
            for(auto u : s[fy])
            {
                int t = u.fi ;
                int cnt = u.se ;
                auto it = s[fx].lower_bound({t , 0}) ;
                if(it != s[fx].end())
                {
                    int tt = (*it).fi ;
                    int num = (*it).se ;
                    if(tt == t)  s[fx].erase(it) , s[fx].insert({tt , num + cnt}) ;
                    else  s[fx].insert(u) ;
                }
                else  s[fx].insert(u) ;
            }
        }
    }
    void update(int x , int y)
    {
        int fx = find(x) ;
        auto it = s[fx].lower_bound({a[x] , 0}) ;
        int t = a[x] ;
        int num = (*it).se ;
        if(num == 1)  s[fx].erase(it) ;
        else  s[fx].erase(it) , s[fx].insert({t , num - 1}) ;
        //del
        ans -= cal(fx , a[x] , 1) ;
        //add

        a[x] = y ;
        ans += cal(fx , a[x] , 1) ;
        it = s[fx].lower_bound({a[x] , 0}) ;
        if(it == s[fx].end())  s[fx].insert({a[x] , 1}) ;
        else
        {
            int t = (*it).fi ;
            int cnt = (*it).se ;
            if(t == a[x])  s[fx].erase(it) , s[fx].insert({t , cnt + 1}) ;
            else  s[fx].insert({a[x] , 1}) ;
        }
    }
} dsu ;
void prework()
{
    dsu.init(n) ;
    rep(b , 1 , 200000)  for(int a = b + b ; a <= 200000 ; a += b)
    {
        int c = a - b ;
        if((a ^ c) == b)  v[a].pb(c) , v[c].pb(a) ;
    }
    rep(i , 1 , n)  s[i].insert({a[i] , 1}) ;
}
int main()
{
    ios ;
    cin >> n >> q ;
    rep(i , 1 , n)  cin >> a[i] ;
    n += q ;
    prework() ;
    while(q --)
    {
        int op , x , y ;
        cin >> op >> x >> y ;
        if(op == 1)  a[x] = y , s[x].insert({y , 1}) ;
        else if(op == 2)  dsu.merge(x , y) ;
        else  dsu.update(x , y) ;
        cout << ans << '\n' ;
    }
    return 0 ;
}