原题链接在这里：https://leetcode.com/problems/critical-connections-in-a-network/

题目：

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

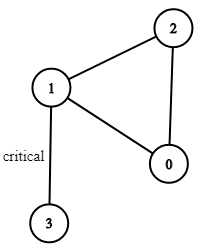
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.

Constraints:

• 1 <= n <= 10^5
• n-1 <= connections.length <= 10^5
• connections[i][0] != connections[i][1]
• There are no repeated connections.

题解：

How to find the bridge of connected graph, we need to find the edge that is not in the cycle.

Then how to find the edge that is not in the cycle. Iterate from one starting node, mark it as visited and the time it has been visited.

Perform DFS for its neighbors, and track the lowest node that this node could reach out to.

When its id < lowest node it could reach out to, then (u, v) is a critical edge.

When meeting a node v that has been visited before, update current node u low with ids[v].

When backtracking, update current node u low with DFS next node v low[v].

Thus DFS state needs to know current node, low array, ids array, graph, res and parent node.

Since this is undirected graph, we want parent to avoid DFS to parent.

Time Complexity: (n + connections.size()). DFS takes O(V + E). each node is only traversed no more than 2 times.

Space: O(v).

AC Java: 

 1 class Solution {
 2     int id = 0;
 3     
 4     public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
 5         List<List<Integer>> res = new ArrayList<>();
 6         if(n < 1){
 7             return res;
 8         }
 9         
10         List<Integer> [] graph = new ArrayList[n];
11         for(int i = 0; i < n; i++){
12             graph[i] = new ArrayList<>();
13         }
14         
15         for(List<Integer> e : connections){
16             graph[e.get(0)].add(e.get(1));
17             graph[e.get(1)].add(e.get(0));
18         }
19         
20         int [] ids = new int[n];
21         Arrays.fill(ids, -1);
22         int [] low = new int[n];
23         
24         for(int i = 0; i < n; i++){
25             if(ids[i] == -1){
26                 dfs(i, low, ids, graph, res, -1);
27             }
28         }
29         
30         return res;
31     }
32     
33     private void dfs(int u, int [] low, int [] ids, List<Integer> [] graph, List<List<Integer>> res, int parent){
34         ids[u] = low[u] = ++id;
35         List<Integer> neibors = graph[u];
36         
37         for(int v : neibors){
38             if(v == parent){
39                 continue;
40             }
41             
42             if(ids[v] == -1){
43                 dfs(v, low, ids, graph, res, u);
44                 low[u] = Math.min(low[u], low[v]);
45                 
46                 if(low[v] > ids[u]){
47                     res.add(Arrays.asList(u, v));
48                 }
49             }else{
50                 low[u] = Math.min(low[u], ids[v]);
51             }
52         }
53     }
54 }