前言
论文网站：http://arxiv.org/abs/1404.3606
论文下载地址：PCANet: A Simple Deep Learning Baseline for Image Classification?
论文的matlab代码（第一个就是）：Matlab Codes for Download
本文的C++ 和 Scala 代码：https://github.com/Ldpe2G/PCANet
该文提出了一个简单的深度学习网络，用于图像分类，用于训练的图像的特征的提取包含以下步骤：
1、cascaded principal component analusis 级联主成分分析；
2、binary hashing 二进制哈希；
3、block-wise histogram 分块直方图
PCA（主成分分析）被用于学习多级滤波器（multistage filter banks），
然后用binary hashing 和 block histograms分别做索引和合并。
最后得出每一张训练图片的特征，每张图片的特征化为 1 x n 维向量，然后用这些特征向量来训练
支持向量机，然后用于图像分类。
正文
=====
训练过程
首先假设我们的训练图片的为N张，
，每张图片大小为 m x n。
第一阶段的主成分分析
首先对每一幅训练图像做一个处理，就是按像素来做一个分块，分块大小为 k1 x k2。
上图解释什么事按像素分块，假设图像是灰度图大小为 5 x 5，分块大小为 2 x 2。
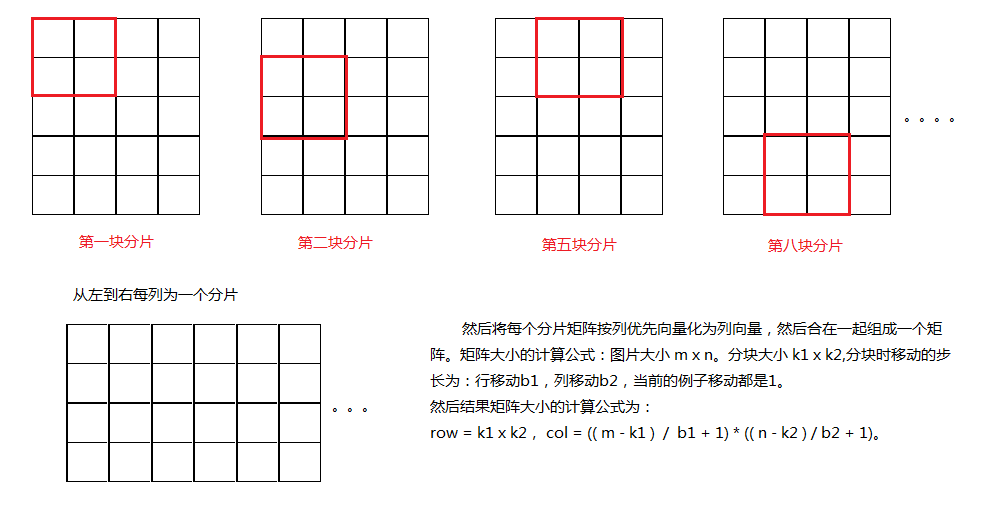
然后得到的分片矩阵大小是 4 x 16，按照上述计算公式可以得到。
然后如果图像是RGB 图像，则首先将三个通道分开，每个通道都做上 诉的分片，得到的分块矩阵，
做一个竖直方向上的合并得到RGB图像的分块矩阵，则如果RGB图像大小为 5 x 5，分块大小2x2，
则得到的分块矩阵大小为 12 x 16。
需要注意的是按照论文的说法，分块的矩阵的列数为m*n，所以5x5矩阵的分块矩阵应该有25列，
但是从代码的实现上看，是按照上图的公式来计算的。
假设第 i 张图片，
，分块后得到的矩阵为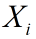 
，然后对每一列减去列平均，得到
。
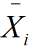接着对N张训练图片都做这样一个处理，得到
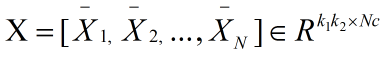
c为分快矩阵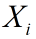的列数。
然后接着求解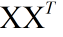
的特征向量，取前
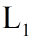个最大的特征值对应的特征向量。
作为下一阶段的滤波器。数学表达为：
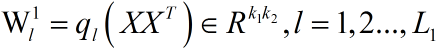
然后第一阶段的主成分分析就完成了。因为我将matlab代码移植到了opencv，所以对原来的代码
比较熟悉，这是结合代码来发分析的，代码实现和论文的描述有些不同。
第二阶段的主成分分析
过程基本上和第一阶段一样。不同的是第一阶段输入的N幅图像要和第一阶段得到的滤波器
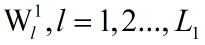分别做卷积，得到 L1 x N 张第二阶段的训练图片。
。
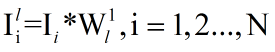在卷积之前首先做一个0边界填充，使得卷积之后的图片和大小相同。
同样对每一张图片做分块处理，然后把由N张图片和L1 个滤波器卷积得到的图片的
分块结果合在一起，首先得到：
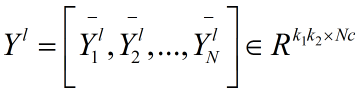
这是N张图片和其中一个滤波器卷积的分块结果。
然后将所有的滤波器输出合在一起：
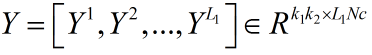
但实际上在代码的实现上，同一张图片 对应的所有滤波器的卷积是放在一起的，
其实就是顺序的不同，对结果的计算没有影响。
然后求解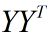
的特征向量，取前
个最大的特征值对应的特征向量。
作为滤波器。
哈希和直方图
然后就来到特征训练的最后一步了。
然后对每一幅第二阶段主成分分析的输入图片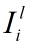
做以下计算：
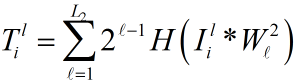
每张图片和L2个滤波器分别进行卷积。H(.)函数表示将一个矩阵转换为一个相同大小的
只包含0和1的矩阵，就是原来元素大于0，则新的矩阵对应的位置为1，否则为0.
然后乘以一个权值再加起来。权值由小到大依次对应的滤波器的也是由小到大。
然后对矩阵
,将其分成B块，得到的分块矩阵大小为 k1k2 x B，
然后统计分块矩阵的直方图矩阵，直方图的范围是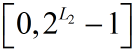
,
直方图矩阵大小为 2^L2 x B。
然后将直方图矩阵向量化为行向量得到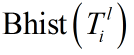
，
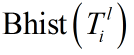最后将所有的的链接起来
得到代表每张训练图的特征向量。
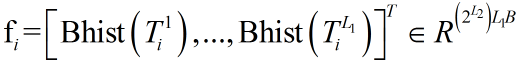
上图解释直方图统计：
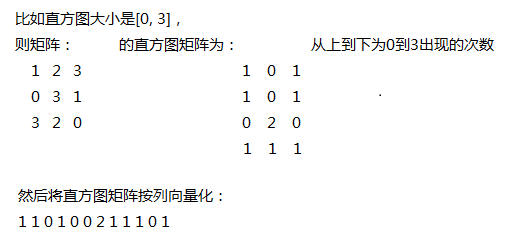
然后训练的步骤就完成了。
接着开始支持向量机的训练和测试。
测试&结果
svm的核函数用的是线性核函数，论文的matlab用的是Liblinear，
由国立台湾大学的Chih-Jen Lin博士开发的，主要是应对large-scale的data classification。
然后opencv的svm的类型我选择了CvSVM::C_SVC，参数C设为1。
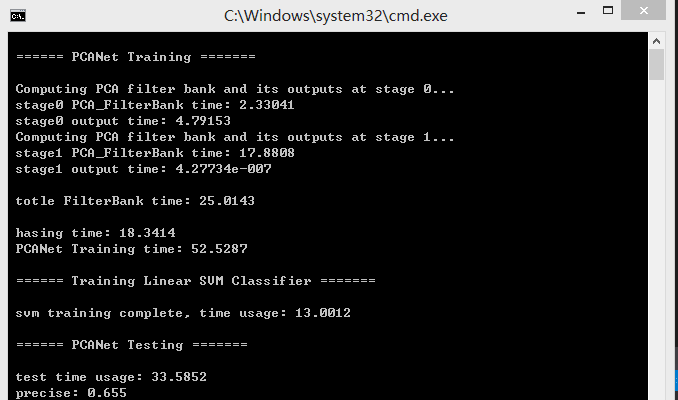
这是我将论文的matlab代码移植到opencv的测试结果，
用了120张图片作测试，精确度为65.5%，比论文中用同样的数据集caltech101，
得到的精度68%要差一点。
对SVM有兴趣的读者可以参考这位博主的文章：
