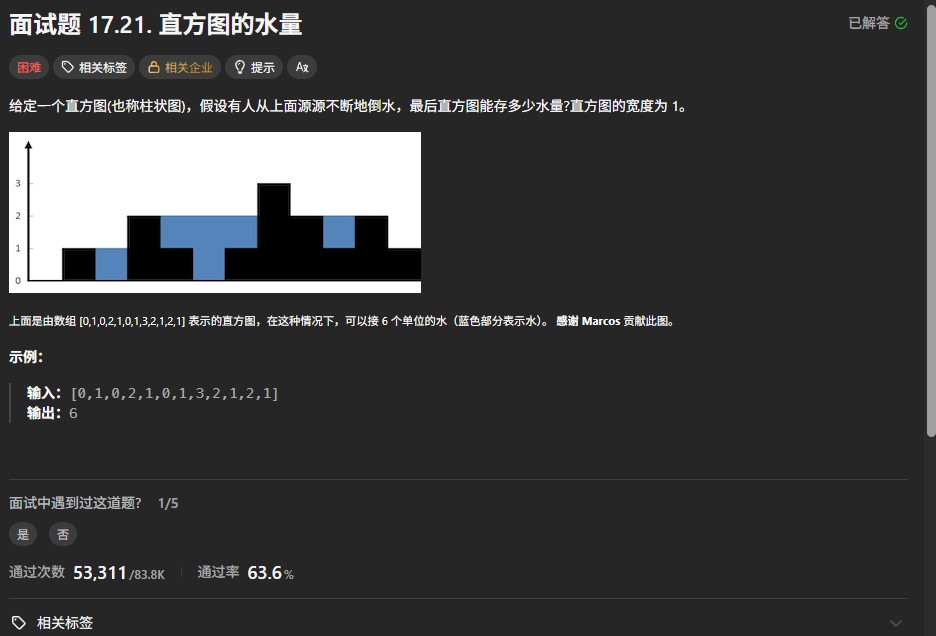
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

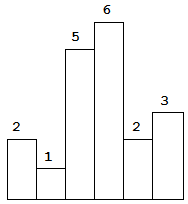
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

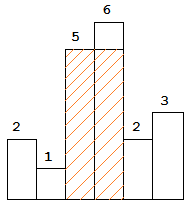
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

输入: [2,1,5,6,2,3]
输出: 10算法：单调栈。此题是利用栈来解决问题最经典的题目之一。我们可以观察得出，矩形所围成的最大面积取决于它左边跟右边第一个小的矩形的长，为此我们可以维护一个单调栈

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n=heights.size(),ans=0;
        heights.push_back(-1);
        stack<int>stk;
        for(int i=0;i<=n;i++){
            while(!stk.empty()&&heights[i]<heights[stk.top()]){
                int cur=stk.top();
                stk.pop();
                if(stk.empty())
                    ans=max(ans,heights[cur]*i);
                else
                    ans=max(ans,heights[cur]*(i-stk.top()-1));
            }
            stk.push(i);
        }
        return ans;
    }
};