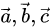向量相加
我们能够通过分别把两个向量的各个分量相加得到向量之和,注意在相加之前必须保证它们有相同的维数。
u + v = (_ux_+ vx, _uy_+ vy, _uz_+ vz)
图5显示的是几何学上的向量相加。
两个向量相加的代码,我们使用重载的加法操作符:
D3DXVECTOR3 u(2.0f, 0.0f, 1.0f);
D3DXVECTOR3 v(0.0f, -1.0f, 5.0f);
// (2.0 + 0.0, 0.0 + (-1.0), 1.0 + 5.0)
D3DXVECTOR3 sum = u + v; // = (2.0f, -1.0f, 6.0f)
向量相减
和加法类似,通过分别把两个向量的各个分量相减得到向量之差。再次重声两个向量必须是相同维数。
u-v = u + (-v) = (ux - vx, uy - vy, uz - vz)
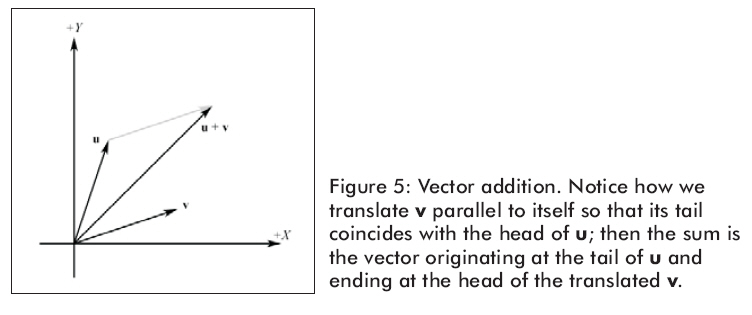
图6显示的是几何学上的向量相减。
两个向量相减的代码,我们使用重载的减法操作符:
D3DXVECTOR3 u(2.0f, 0.0f, 1.0f);
D3DXVECTOR3 v(0.0f, -1.0f, 5.0f);
D3DXVECTOR3 difference = u - v; // = (2.0f, 1.0f, -4.0f)
图6显示,向量减法得到一个从v向量终点到u向量终点的向量。假如我们解释u和v的分量,我们能用向量相减找到从一个点到另一个点的向量。这是非常方便的操作,因为我们常常想找到从一个点到另一个点的方向向量。
标量与向量的乘积
我们能用一个标量与向量相乘,就象名字暗示的一样,向量按比例变化。这种运算不会改变向量的方向,除非标量是负数,这种情况向量方向相反。
ku = (kux, kuy, kuz)
D3DXVECTOR3类提供了向量与标量乘法的操作符。
D3DXVECTOR3 u(1.0f, 1.0f, -1.0f);
D3DXVECTOR3 scaledVec = u * 10.0f; // = (10.0f, 10.0f, -10.0f)
点积
数学上定义点积是两个向量的乘积。按下面等式计算:
u.v = uxvx + uyvy + uzvz = s
The above formula does not present an obvious geometric meaning. Using the law of cosines, we can find the relationship u.v = ∥u∥∥v∥ cosθ , which says that the dot product between two vectors is the cosine of the angle between them scaled by the vectors' magnitudes. Thus, if both u and v are unit vectors, then u.v is the cosine of the angle between them.
Some useful properties of the dot product:
If u.v = 0, then u ⊥ v.
If u.v > 0, then the angle θ, between the two vectors is less than 90 degrees.
If u.v < 0, then the angle θ, between the two vectors is greater than 90 degrees.
Note
The ⊥ symbol means "orthogonal," which is synonymous with the term "perpendicular."
We use the following D3DX function to compute the dot product between two vectors:
FLOAT D3DXVec3Dot( // Returns the result. CONST D3DXVECTOR3* pV1, // Left sided operand. CONST D3DXVECTOR3* pV2 // Right sided operand.);D3DXVECTOR3 u(1.0f, -1.0f, 0.0f);D3DXVECTOR3 v(3.0f, 2.0f, 1.0f);// 1.0*3.0 + -1.0*2.0 + 0.0*1.0// = 3.0 + -2.0float dot = D3DXVec3Dot( &u, &v ); // = 1.0
叉积
第二种乘法在向量数学中叫叉积。不象点积,结果值是一个标量,叉积的结果值是另一个向量。通过把两个向量u和v相乘得到另一的向量p,向量p垂直于u和v。也就是说向量p垂直于u并且垂直于u。
The cross product is computed like so:
p = u×v = [(uyvz - uzvy), (uzvx - uxvz), (uxvy - uyvx)]
In component form:
px = (uyvz - uzvy)
py = (uzvx - uxvz)
_p_z = (uxvy - uyvx)
Example: Find j = k × i = (0, 0, 1) × (1, 0, 0) and verify that j is orthogonal to both k and i.
Solution:
jx =(0(0)-1(0)) = 0
jy =(1(1)-0(0) = 1
_j_z=(0(0)-0(1) = 0
So, j = (0, 1, 0). Recall from the section titled "Dot Products" that if u.v = 0, then u ⊥ v Since j.k = 0 and j.i = 0, we know j is orthogonal to both k and i.
We use the following D3DX function to compute the cross product between two vectors:
D3DXVECTOR3 *D3DXVec3Cross( D3DXVECTOR3* pOut, // Result. CONST D3DXVECTOR3* pV1, // Left sided operand. CONST D3DXVECTOR3* pV2 // Right sided operand.);
It is obvious from Figure 7 that the vector -p is also mutually orthogonal to both u and v. The order in which we perform the cross product determines whether we get p or -p as a result. In other words, u × v = -(v × u). This shows that the cross product is not commutative. You can determine the vector returned by the cross product by the left hand thumb rule. (We use a left hand rule because we are using a left-handed coordinate system. We would switch to the right hand rule if we were using a right-handed coordinate system.) If you curve the fingers of your left hand in the direction of the first vector toward the second vector, your thumb points in the direction of the returned vector.