01
说明
接上一篇《 Fama-French三因子回归A股实证 》,继续写Carhart四因子模型,整个过程比较容易,还是基于Fama三因子的框架,多加进去一个动量因子进行回归。全文的代码数据论文获取请在后台回复“C4"。
贴上论文原文对于模型的说明如下

三行公式,第一行为CAPM,第二行为Fama三因子模型,第三行为四因子模型,其中,RMRF是市场因子,也就是我们上一篇中的MKT,PR1YRt是作者构建的动量因子,本文我们用UMD表示。
对于动量因子的定义,原文说明如下,黄字部分

解释一下, 每月末计算所有股票前2-12个月末的收益率,构建投资组合:前30%的等权组合,后30%的等权组合,二者收益率的差值定义为动量因子,组合月度调整 。
从定义来看,和Fama三因子的差异主要有两点,首先是 组合是等权的 ,Fama三因子中的组合都是市值加权的,其次 组合是月度构建的 ,三因子中的组合的年度构建的。最后需要说明一点,这里用2-12个月的收益率实际上是剔除了最近1个月的收益率,原因主要在于美股市场是短期反转,长期动量的,剃掉最近1个月的反转,可以得到比较纯粹的动量。
之后的部分和Fama三因子差不多了,因变量相同,自变量多一个动量因子,这里我们沿用上一篇的方式进行回归,构建25个投资组合,做25次回归(原文回归的过程不是这样做的,细节可以参考原文)。
02
实证部分
数据还是之前用的那些,没有变化,先给出动量因子的计算过程。首先每个月末把所有上市公司按前2-12个月末的收益率分为三层
# 动量因子UMD
def split_UMD(
x):
x.
loc[
x[
'UMD'] >=
x.UMD.quantile(
0.7),
'group_UMD'] =
'UMD_H'
x.
loc[
x[
'UMD'] <
x.UMD.quantile(
0.3),
'group_UMD'] =
'UMD_L'
return
x
UMD = price.pivot(
index =
'tradedate',columns =
'stockcode',
values =
'price').pct_change(
11).shift(
1).fillna(
0)
UMD = UMD.stack().reset_index()
UMD = UMD.
rename(columns = {UMD.columns[
2]:
'UMD'})
f[
'group_UMD'] =
'UMD_M'
f = pd.merge(
f,UMD,left_on =[
'stockcode',
'tradedate'],right_on =[
'stockcode',
'tradedate'])
f =
f .groupby([
'ym']).apply(split_UMD)
计算最大组和最小组的等权收益率差值作为动量因子
# UMD因子
UMD_ret = f.groupby([
'tradedate',
'group_UMD']).apply(lambda x:x.ret.mean())
UMD_ret = UMD_ret.reset_index()
UMD_ret = UMD_ret.rename(columns = {UMD_ret.columns[-
1]:
'ret'})
UMD_ret_pivot = UMD_ret.pivot(index =
'tradedate',columns =
'group_UMD',values =
'ret')
UMD = UMD_ret_pivot[
'UMD_H'] - UMD_ret_pivot[
'UMD_L']
最后再把UMD因子和fama三因子进行合并,fama三因子的计算过程略去,可以看文章开头的链接
Carhart4 = pd.concat([SMB,HML,UMD],axis =
1)
Carhart4 = Carhart4.reset_index()
Carhart4.columns = [
'tradedate',
'SMB',
'HML',
'UMD']
Carhart4[
'ym'] = Carhart4.tradedate.apply(
lambda x:x.year*
100 + x.month)
首先看看四个因子的收益曲线
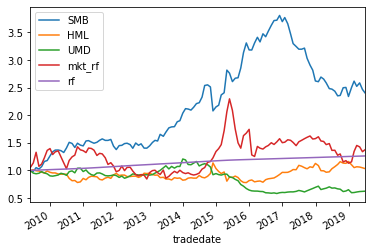
可以明显看出,A股是没啥动量的,反转要显著一点。
个人粗浅的理解,反转一定程度上可以表示投机性的程度。A股的反转比较显著,这和A股的投资者结构关系比较大,主要为个人投资者,投机性更强一些。而且反转因子具有明显的收益集中在空头的特征,实际上和投机的心理非常一致:投资者非常可能在获得很高的收益后马上平仓,规避风险,而在股票暴跌很多时候去抄底承担风险的,虽然也有,但肯定比前者要少很多。当然,反转的不对称性也和A股不能做空有很大的关系。
接下来看看四个因子的相关性情况
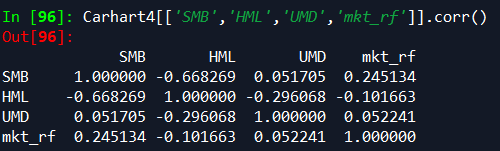
动量因子和其他三个因子的相关性都很低。
接下来做四因子回归,代码和之前也是基本类似的
### 四因子回归
x = f25.
loc[:,[
'SMB',
'HML',
'UMD',
'mkt_rf',
'Intercept']].
values
r2 = []
betas = []
t = []
p = []
for i in
range(
25):# i =
0
y = f25.
loc[:,f25.columns[i+
1]].
values
mod =
sm.OLS(
y,
x).fit()
r2.
append([f25.columns[i+
1],
mod.rsquared])
betas.
append([f25.columns[i+
1]] +
list(
mod.params))
t.
append([f25.columns[i+
1]] +
list(
mod.tvalues))
p.
append([f25.columns[i+
1]] +
list(
mod.pvalues))
p = pd.DataFrame(
p,columns = [
'group',
'SMB',
'HML',
'UMD',
'mkt_rf',
'Intercept'])
t = pd.DataFrame(t,columns = [
'group',
'SMB',
'HML',
'UMD',
'mkt_rf',
'Intercept'])
betas = pd.DataFrame(betas,columns = [
'group',
'SMB',
'UMD',
'HML',
'mkt_rf',
'Intercept'])
r2 = pd.DataFrame(r2,columns = [
'group',
'r2'])
p_percent_car4 = (
p.iloc[:,
1:]<
0.05).mean()
alpha = betas[[
'group',
'Intercept']]
alpha[
'g_BM'] = alpha.group.apply(lambda
x:
x[
2])
alpha[
'g_SIZE'] = alpha.group.apply(lambda
x:
x[-
1])
alpha = alpha.pivot(
index =
'g_SIZE',columns =
'g_BM',
values =
'Intercept')
alpha = alpha.reset_index()
alpha = alpha.
rename(columns = {
'g_SIZE':
'',
alpha.columns[
1]:
'small BM',
alpha.columns[-
1]:
'big BM'})
alpha.iloc[
0,
0] =
'small SIZE'
alpha.iloc[-
1,
0] =
'big SIZE'
alpha
返回回归的p值、beta、r2、alpha。
对于四因子模型,主要说明三点:
首先,看回归的系数beta:
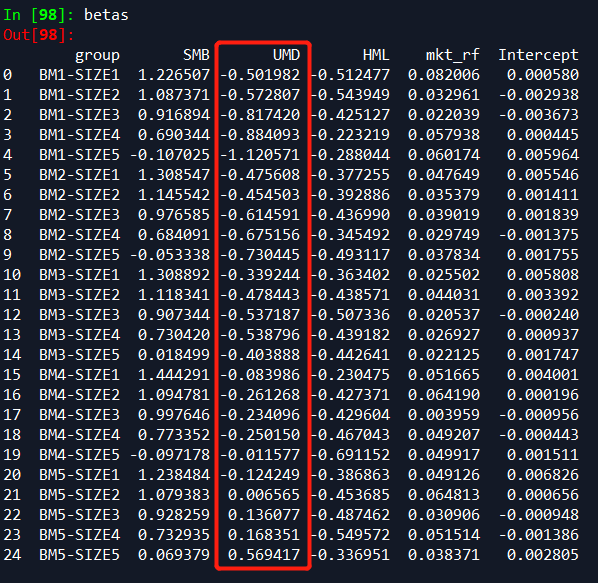
大部分回归里,动量的系数为负,再次说明主要是反转的贡献,不是动量。
其次,四因子回归系数的p值
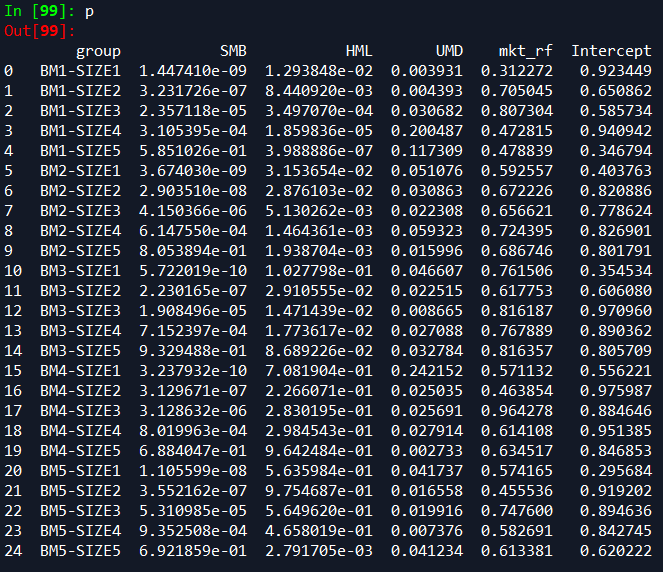
统计其中5%显著性显著的回归个数
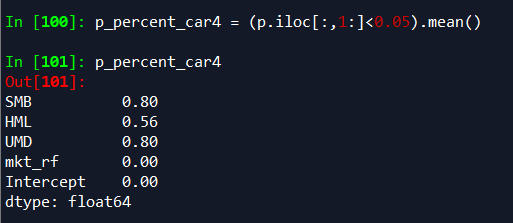
与三因子回归中显著的回归个数进行对比
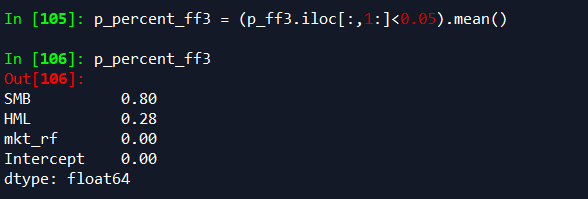
可以看出,在加入UMD因子之后,系数的显著性没有降低。
类似的,统计三因子和四因子的25次回归里整体F检验的p值
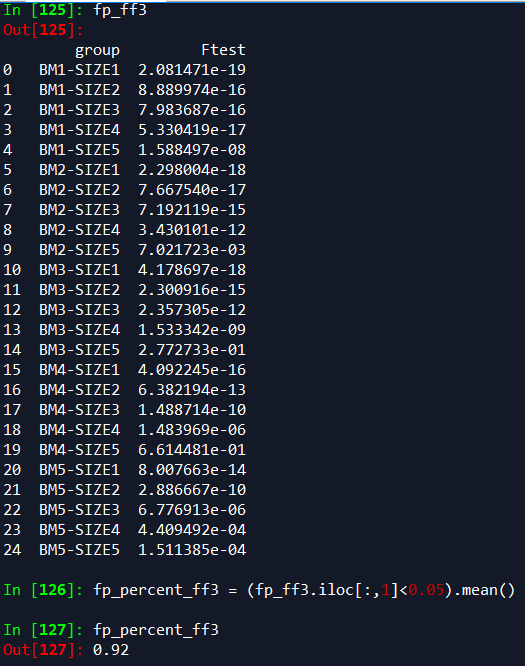
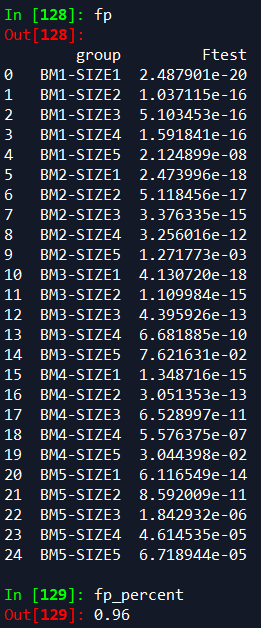
也能看出,加入动量因子前, 92% 的回归是显著的,加入后, 96% 的回归是显著的,这说明 动 量因子确实包含有一些三因子模型无法解释的信息,可以提升三因子模型的效果 。
03
最后
最后,也可以类比《 基于Fama三因子的因子构建 》一文,去构建基于四因子的相关因子,但从相关券商报告的结论来看,效果没有非常好的改善,所以也没有做过多的尝试,如果有兴趣,欢迎交流。
参考文献
Carhart M M. On persistence in mutual fund performance[J]. The Journal of finance, 1997, 52(1): 57-82.
本文分享自微信公众号 - 数据科学实战(dsaction)。
如有侵权,请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”,欢迎正在阅读的你也加入,一起分享。












