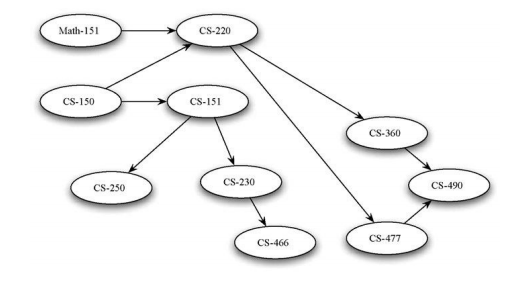
Python数据结构与算法——图 - HelloWorld开发者社区

图的定义

Python数据结构与算法——图

图（graph）是由一些点（vertex）和这些点之间的连线（edge）所组成的；其中，点通常称为顶点（vertex），而点到点之间的连线通常称之为边或者弧（edge）。通常记为G=（V,E）。

要注意的是：线性表可以是空表，树可以是空树，图不可以是空图，图可以没有边，但是至少要有一个顶点。

图的术语

顶点

顶点⼜称节点，是图的基础部分。它可以有⾃⼰的名字，我们称作“键”。顶点也可以带有附加信息，我们称作“有效载荷”。

边

边是图的另⼀个基础部分。两个顶点通过⼀条边相连，表⽰它们之间存在关系。边既可以是单向的，也可以是双向的。如果图中的所有边都是单向的，我们称之为有向图。

权重

边可以带权重，⽤来表⽰从⼀个顶点到另⼀个顶点的成本。例如在路线图中，从⼀个城市到另⼀个城市，边的权重可以表⽰两个城市之间的距离。

路径

无论是无向图还是有向图，从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点），称为一条路径。

环

如果路径中第一个顶点和最后一个顶点相同，则此路径称为"环"（或"回路"）。

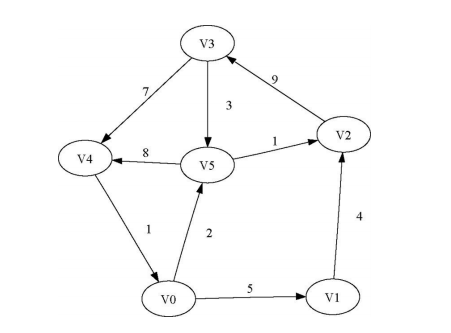
Python数据结构与算法——图

图的实现

可以通过多种⽅式在Python中实现图的抽象数据类型。你会看到，在使⽤不同的表达⽅式来实现图的抽象数据类型时，需要做很多取舍。有两种⾮常著名的图实现，它们分别是邻接矩阵和邻接表。本节会解释这两种实现，并且⽤Python类来实现邻接表。

邻接矩阵

要实现图，最简单的⽅式就是使⽤⼆维矩阵。在矩阵实现中，每⼀⾏和每⼀列都表⽰图中的⼀个顶点。第 V ⾏和第 W 列交叉的格⼦中的值表⽰从顶点V 到顶点W 的边的权重。如果两个顶点被⼀条边连接起来，就称它们是相邻的。

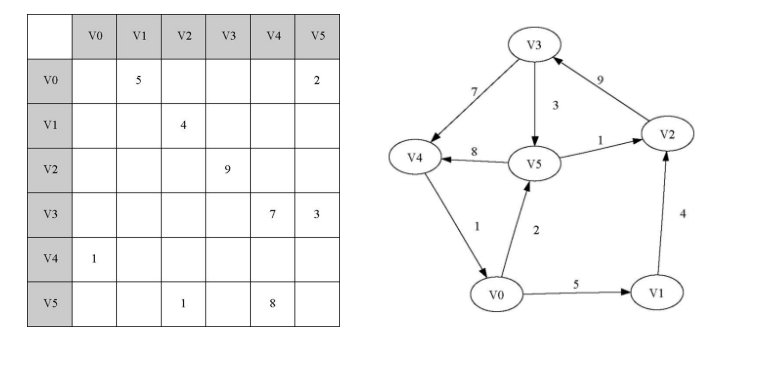
Python数据结构与算法——图

优点

简单。对于⼩图来说，邻接矩阵可以清晰地展⽰哪些顶点是相连的。

缺点

对于存储稀疏数据来说，矩阵并不⾼效。

邻接表

为了实现稀疏连接的图，更⾼效的⽅式是使⽤邻接表。在邻接表实现中，我们为图对象的所有顶点保存⼀个主列表，同时为每⼀个顶点对象都维护⼀个列表，其中记录了与它相连的顶点。在对Vertex 类的实现中，我们使⽤字典（⽽不是列表），字典的键是顶点，值是权重。

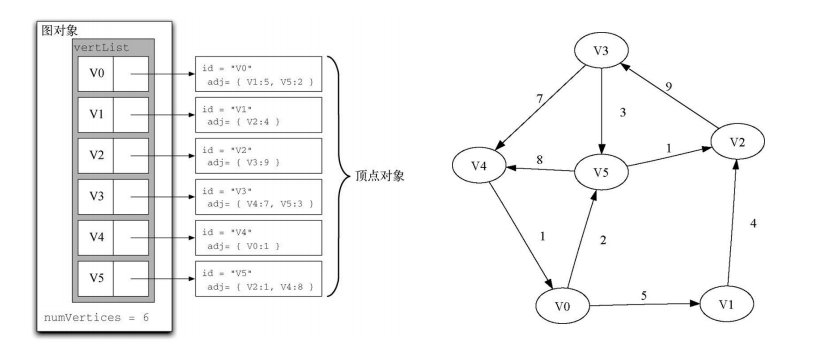
Python数据结构与算法——图

优点

能够紧凑地表⽰稀疏图。此外，邻接表也有助于⽅便地找到与某⼀个顶点相连的其他所有顶点。

图的代码实现

class Graph:

    def __init__(self):
        self.vertices = {}
        self.num_of_vertices = 0

    def add_vertex(self, key):
        new_vertex = Vertex(key)
        self.vertices[key] = new_vertex
        self.num_of_vertices = self.num_of_vertices + 1

        return new_vertex

    def get_vertex(self, n):
        if n in self.vertices:
            return self.vertices[n]
        return None

    def contains(self, n):
        return n in self.vertices

    def add_edge(self, f, t, cost=0):
        if f not in self.vertices:
            new_vertex = self.add_vertex(f)

        if t not in self.vertices:
            new_vertex = self.add_vertex(t)

        self.vertices[f].add_neighbor(self.vertices[t], cost)

    def get_vertices(self):
        return self.vertices.keys()

    def __iter__(self):
        return iter(self.vertices.values())


class Vertex:

    def __init__(self, key):
        self.id = key
        self.connect_to = {}

    def add_neighbor(self, nbr, weight=0):
        self.connect_to[nbr] = weight

    def __str__(self):
        return str(self.id) + "connect to" + str([x.id for x in self.connect_to])

    def get_id(self):
        return self.id

    def get_connections(self):
        return self.connect_to.keys()

    def get_weight(self, nbr):
        return self.connect_to[nbr]