2019牛客多校第一场 I Points Division（动态规划+线段树）

传送门：https://ac.nowcoder.com/acm/contest/881/I

题意：

给你n个点，每个点有两个属性a,b

需要将点划分为两堆，划分依据是对于在A划分中的任意点a和在B划分中的任意点b满足

不存在当a.x>b.x时,a.y<b.y 的情况

在A划分中的点可以给出其a属性的贡献，在B划分中的点可以给出其b属性的贡献

求最大贡献和

题解：

根据题意，我们可以得出结论，我们需要找的是一根折线，这根折线将点集分为A、B两部分、

我们需要求这两个部分的最大权值和

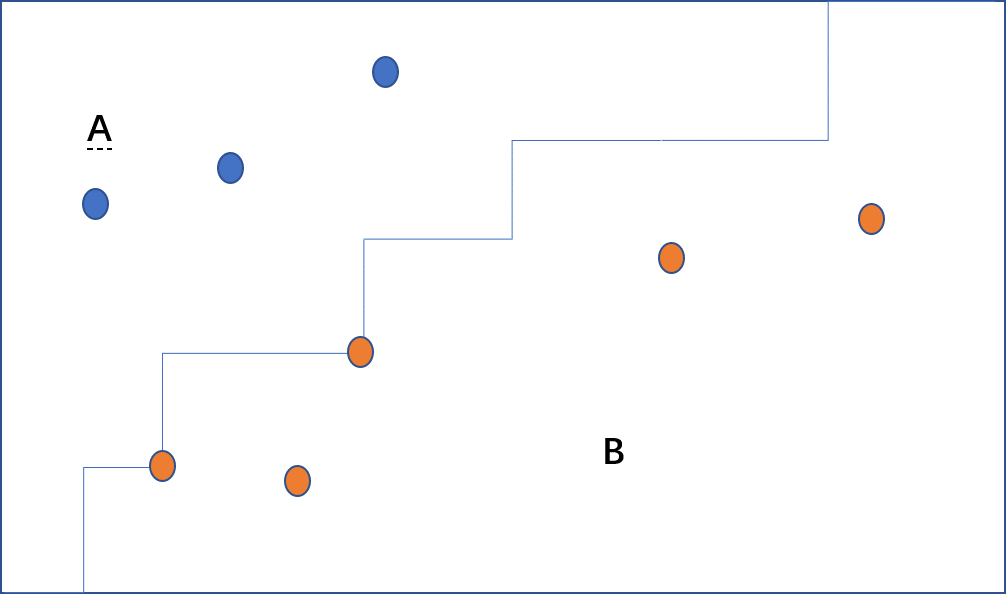
我们考虑dp状态

dp[i]表示到第i个点在折线上时和的最大值，如果增加了这个点，他对答案产生的贡献就是，对于之前比这个点高的点，对答案的贡献是ai，对于之前比这个点低的点，对答案的贡献是bi

于是$d p[j]=\left{\begin{array}{ll}{d p[j]+b_{i}} & {j<i, y_{j}>y_{i}} \ {d p[j]+a_{i}} & {j<i, y_{j}<y_{i}}\end{array}\right.$

$d p[i]=b_{i}+\max {1 \leq j<i, y{j}<y_{i}} d p[j]$

显然这个式子是可以用线段树维护区间最值的

因为值域范围为1e9，我们将y值离散化后建树，维护的区间最大值就是我们最后的答案

因为dp的值是从0开始的，所以我们建树也是从0开始

排序是为了能够有A，B的合法划分

感谢邱神的博客学习：https://blog.csdn.net/u013534123/article/details/96465704

代码：

#include <set>
#include <map>
#include <cmath>
#include <cstdio>
#include <string>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********\n")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]\n"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]\n"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]\n"
const int maxn = 3e5 + 5;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
LL quick_pow(LL x, LL y) {
    LL ans = 1;
    while(y) {
        if(y & 1) {
            ans = ans * x % mod;
        } x = x * x % mod;
        y >>= 1;
    } return ans;
}
LL Max[maxn << 2];
LL lazy[maxn << 2];
void push_up(int rt) {
    Max[rt] = max(Max[ls], Max[rs]);
}
void build(int l, int r, int rt) {
    Max[rt] = lazy[rt] = 0;
    if(l == r) return;
    int mid = (l + r) >> 1;
    build(lson);
    build(rson);
}
void push_down(int rt) {
    if(lazy[rt]) {
        lazy[ls] += lazy[rt];
        lazy[rs] += lazy[rt];
        Max[ls] += lazy[rt];
        Max[rs] += lazy[rt];
        lazy[rt] = 0;
    }
}
void update(int L, int R, LL val, int l, int r, int rt) {
    if(L <= l && r <= R) {
        Max[rt] += val;
        lazy[rt] += val;
        return;
    }
    push_down(rt);
    int mid = (l + r) >> 1;
    if(L <= mid) update(L, R, val, lson);
    if(R > mid) update(L, R, val, rson);
    push_up(rt);
}
void change(int pos, LL val, int l, int r, int rt) {
    if(l == r) {
        Max[rt] =  val;
        return;
    }
    push_down(rt);
    int mid = (l + r) >> 1;
    if(pos <= mid) change(pos, val, lson);
    else change(pos, val, rson);
    push_up(rt);
}
LL query(int L, int R, int l, int r, int rt) {
    if(L <= l && r <= R) {
        return Max[rt];
    }
    push_down(rt);
    int mid = (l + r) >> 1;
    LL ans = 0;
    if(L <= mid) ans = max(ans, query(L, R, lson));
    if(R > mid) ans = max(ans, query(L, R, rson));
    return ans;
}
struct node {
    int x, y, a, b;
} p[maxn];
bool cmp(node a, node b) {
    if(a.x != b.x) return a.x < b.x;
    return a.y > b.y;
}
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    int n;
    while(~scanf("%d", &n)) {
        vector<int> vec;
        for(int i = 1; i <= n; i++) {
            scanf("%d%d%d%d", &p[i].x, &p[i].y, &p[i].a, &p[i].b);
            vec.push_back(p[i].y);
        }
        sort(vec.begin(), vec.end());
        vec.erase(unique(vec.begin(), vec.end()), vec.end());
        for(int i = 1; i <= n; i++) {
            p[i].y = lower_bound(vec.begin(), vec.end(), p[i].y) - vec.begin() + 1;
        }
        int tot = vec.size();
        sort(p + 1, p + n + 1, cmp);
        build(0, tot, 1);
        for(int i = 1; i <= n; i++) {
            change(p[i].y, query(0, p[i].y, 0, tot, 1) + p[i].b, 0, tot, 1);
            if(p[i].y - 1 >= 0) update(0, p[i].y - 1, p[i].a, 0, tot, 1);
            if(p[i].y + 1 <= tot) update(p[i].y + 1, tot, p[i].b, 0, tot, 1);
        }
        printf("%lld\n", Max[1]);
    }


    return 0;
}