首先我们知道基本类型只能表示一定范围内的数值。
byte (-128-127);
long (-9223372036854774808~9223372036854774807)
如果超出范围了该怎么办呢? 比如如何来表示 123123456789123456789。
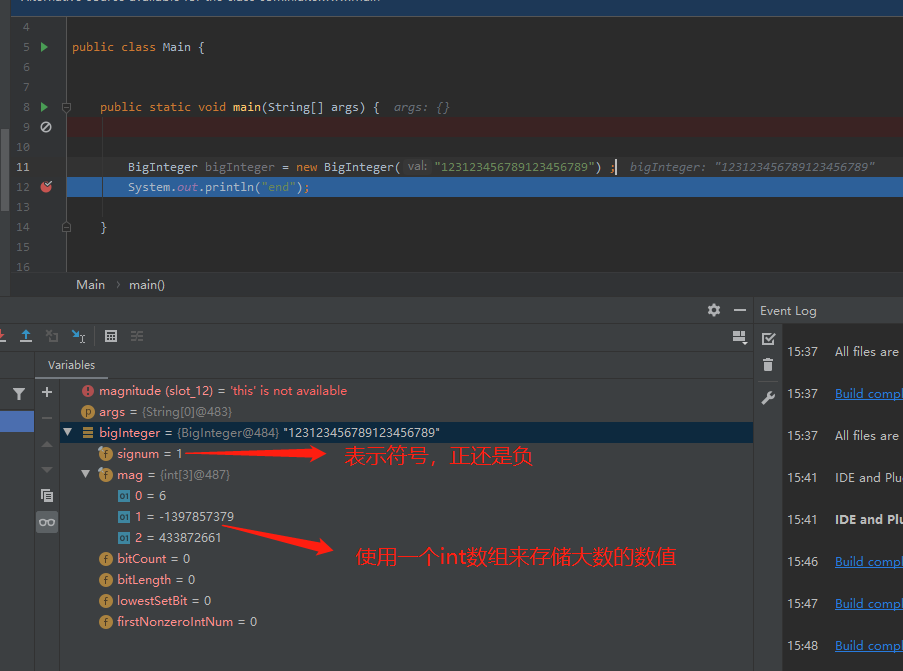
更正一下 ,signum 有三个取值 1,0,-1 .
mag 数组的定义是什么?
首先大数 123123456789123456789 对应的二进制为 1101010110010101110011000111001110100011001110111000101111100010101 , 共67位, 从后往前每32个bit位可以当作一个int进行存储 。 这应该是最节约内存的表示方式了 ,表示这个大数占用了16个字节 。
char[] arr = {'1','2','3','1','2','3','4','5','6','7','8','9','1','2','3','4','5','6','7','8','9'}; 占用42个字节,所以不大会直接用一个char数组来表示大数

以下是计算出mag数组的算法,这是一个非常有意思的处理过程。
相信大家对如何将字符串“123” 转化为10进制整形123已经很熟悉了
public static void main(String[] args) { String a = "123" ; char[] chars = a.toCharArray() ; int sum = 0; int index = 0; while (index<chars.length){ sum = sum * 10 + chars[index] - '0'; index++; } System.out.println(sum); }
以下转换思路类似,只是稍微麻烦了一些些 。
1: 将123123456789123456789 分为三组 group0 = 123 , group1 = 123456789, group2 = 123456789 ;
其中group0 的长度为大数的length % 9, 其余 group的长度均为9 , 这个和 java int 的表示范围有关 。Integer.MAX_VALUE = 2147483647 恰好为10位, 因此每组取9个字符,在parse时不会存在溢出问题 。
int[] num = new int[3] ;
2:
2.1 num[2] = group0的int值 ; num[1] = 0 ; num[0] = 0 ;
2.2.1 long x = num[2] * 10 ^ 9 ; 123000000000 ; 一个long刚好8个字节 ,分为两个int存储 , (int) x 为x的后四个字节, x>>>32 为x的前四个字节。
num[2] = (int) x ;
long x = num[1] + x >>> 32 ;
num[1] = (int) x ;
long x = num[0] + x >>> 32 ;
num[0] = (int) x ;
2.2.2 long sum = num[2] + group1的int值
num[2] = (int) sum ;
sum = num[1] + sum >>> 32 ; 有可能有进位
num[1] = (int) sum ;
sum = num[0] + sum >>> 32 ; 有可能有进位
num[0] = (int) sum ;
重复2.2 的两个过程, 即可将一个字符串(大数)表示为整形数组 。
还有一些很细节的问题, 比如mag数组的大小,如果小了,肯定表示不了大数, 但是如果大了,对上面的算法毫无影响,最后只需去掉数组前面值为0的item即可 。
(2^n > 123123456789123456789 先求出最小的n 然后 【n/32 】 理论上是这样的,但是这个是无法实现的,因为此时 123123456789123456789是根本不存在的,如果存在也就不需要再表示了)。
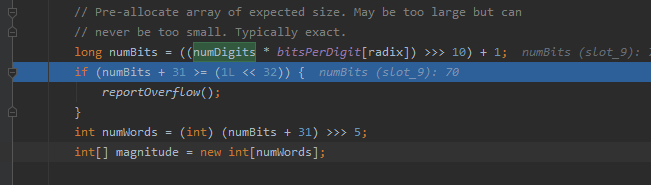
((length * 3402 >>> 10 ) +1 + 31 ) >>> 5 , 为啥这个可以用来估算mag的长度,而且一定比需要的长度大或者等于。 我现在也没有弄明白,充满神秘感的东西才是这个世界上最好的东西 。
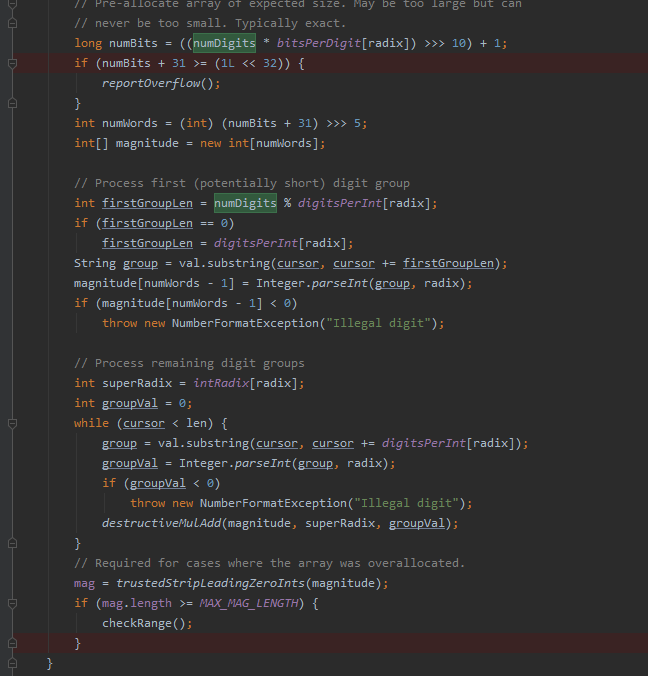
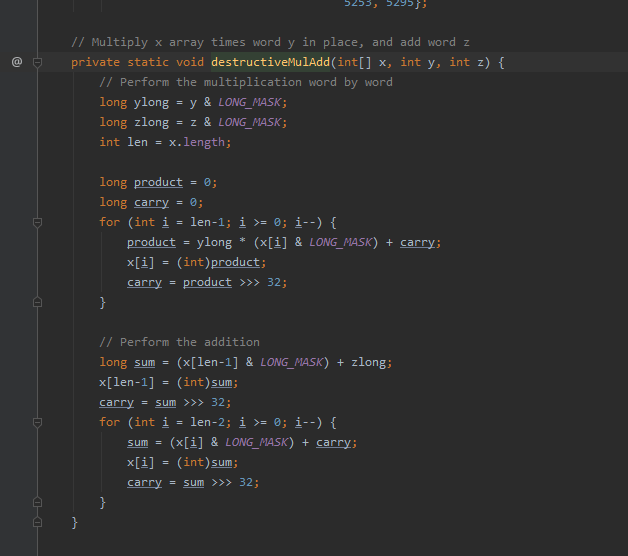
这两个过程我是看了n多遍才慢慢看懂的 。
接下来的问题:
1:如何将mag数组还原成一个字符串?如果不可逆那么这种表示方式没有任何意义。
2:如何实现加减乘除等运算 。














