2018-09-07 09:03:14
一、Merge Intervals
问题描述:
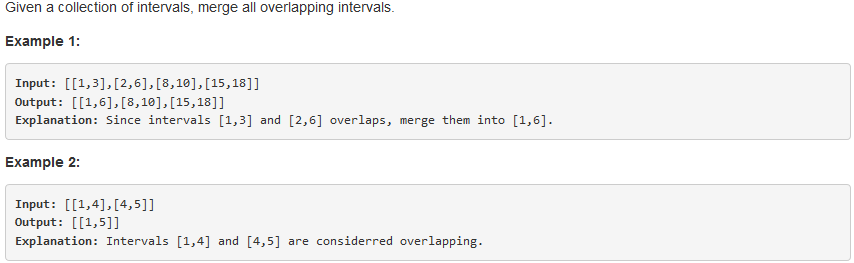
问题求解:
public List<Interval> merge(List<Interval> intervals) {
List<Interval> res = new ArrayList<>();
if (intervals.size() == 0) return res;
Collections.sort(intervals, new Comparator<Interval>() {
public int compare(Interval o1, Interval o2) {
return o1.start - o2.start;
}
});
int start = intervals.get(0).start;
int end = intervals.get(0).end;
for (int i = 1; i < intervals.size(); i++) {
if (intervals.get(i).start > end) {
res.add(new Interval(start, end));
start = intervals.get(i).start;
end = intervals.get(i).end;
}
else {
end = Math.max(end, intervals.get(i).end);
}
}
res.add(new Interval(start, end));
return res;
}
二、Insert Interval
问题描述:

问题求解:
本题的问题描述中明确的说明了,本题的给出条件中的intervals是已经排序好的,并且是没有overlapping的,因此在后续的求解过程中只需要一次遍历即可。
public List<Interval> insert(List<Interval> intervals, Interval newInterval) {
List<Interval> res = new ArrayList<>();
int i = 0;
while (i < intervals.size() && intervals.get(i).end < newInterval.start) {
res.add(intervals.get(i++));
}
while (i < intervals.size() && intervals.get(i).start <= newInterval.end) {
newInterval.start = Math.min(newInterval.start, intervals.get(i).start);
newInterval.end = Math.max(newInterval.end, intervals.get(i).end);
i++;
}
res.add(newInterval);
while (i < intervals.size()) res.add(intervals.get(i++));
return res;
}
三、My Calendar I
问题描述:
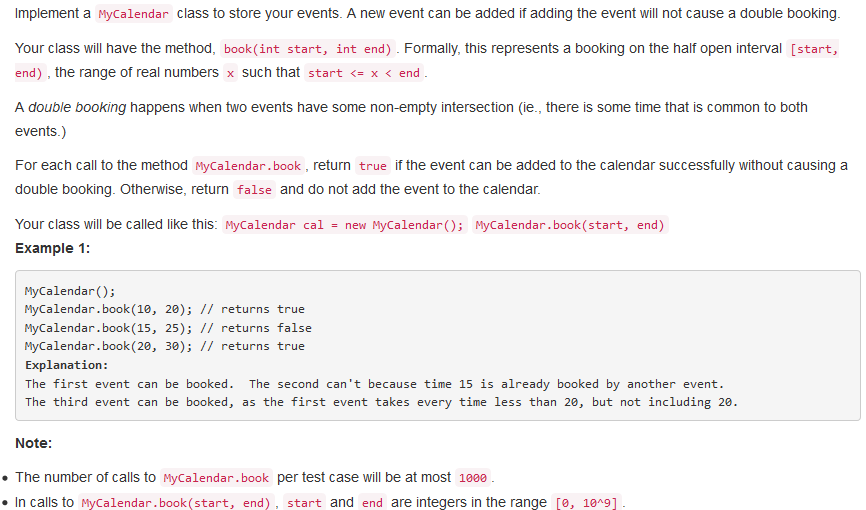
问题求解:
解法一:Boundary Counting
对边界进行计数,最后遍历一遍即可,如果过程中有curSum大于1的情况,则表明出现了overlapping。
如果使用keySet()则会多出log(n)的时间,而本题卡时间非常紧,如果使用key进行提取,则会TLE。
如果使用entrySet(),则会Accept,但是也是将将通过。
public class MyCalendar { TreeMap<Integer, Integer> map; public MyCalendar() { map = new TreeMap<>(); } public boolean book(int start, int end) { return helper(start, end); } private boolean helper(int start, int end) { map.put(start, map.getOrDefault(start, 0) + 1); map.put(end, map.getOrDefault(end, 0) - 1); int curSum = 0; for (Map.Entry<Integer, Integer> entry : map.entrySet()) { curSum += entry.getValue(); if (curSum > 1) { map.put(start, map.get(start) - 1); if (map.get(start) == 0) map.remove(start); map.put(end, map.get(end) + 1); if (map.get(end) == 0) map.remove(end); return false; } } return true; }}
解法二、
记录各个interval,并且所有的interval都是没有overlapping的。
public class MyCalendar { TreeMap<Integer, Integer> treeMap;
public MyCalendar() {
treeMap = new TreeMap<>();
}
public boolean book(int start, int end) {
Integer floor = treeMap.floorKey(start);
if (floor != null && treeMap.get(floor) > start) return false;
Integer ceil = treeMap.ceilingKey(start);
if (ceil != null && ceil < end) return false;
treeMap.put(start, end);
return true;
}}
四、My Calendar II
问题描述:
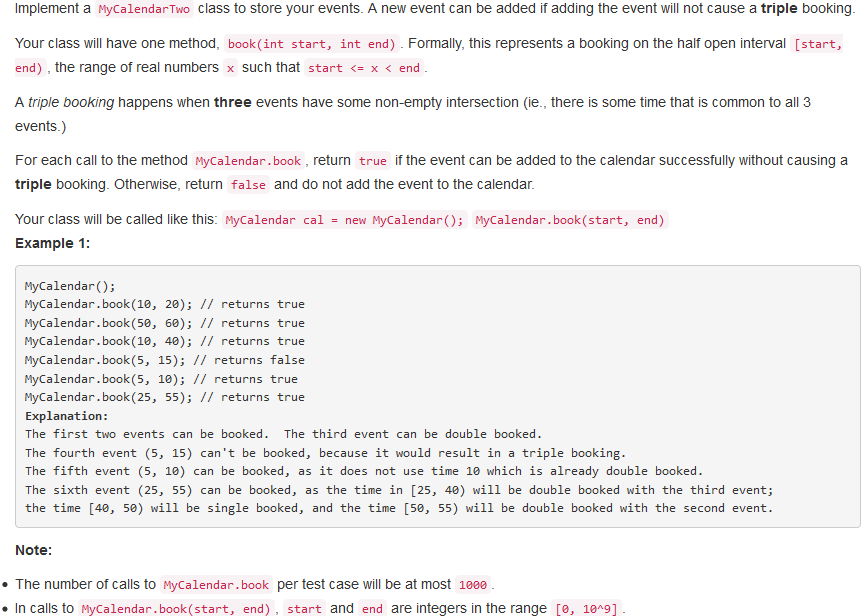
问题求解:
万能的Boundary Counting。
public class MyCalendarTwo {
TreeMap<Integer, Integer> map;
public MyCalendarTwo() {
map = new TreeMap<>();
}
public boolean book(int start, int end) {
map.put(start, map.getOrDefault(start, 0) + 1);
map.put(end, map.getOrDefault(end, 0) - 1);
int cnt = 0;
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
cnt += entry.getValue();
if (cnt > 2) {
map.put(start, map.get(start) - 1);
if (map.get(start) == 0) map.remove(start);
map.put(end, map.get(end) + 1);
if (map.get(end) == 0) map.remove(end);
return false;
}
}
return true;
}
}
五、My Calendar III
问题描述:
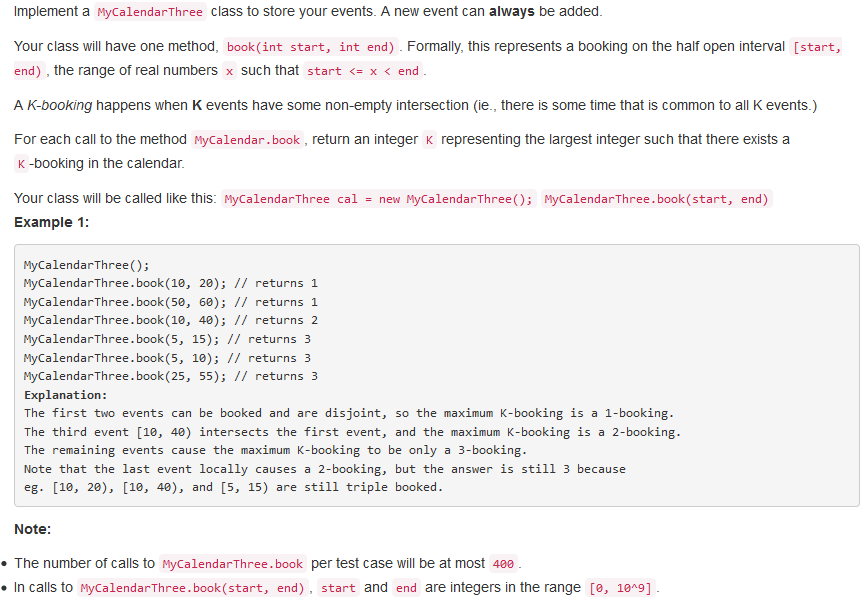
问题求解:
解法一:
万能的Boundary Counting。
public class MyCalendarThree {
TreeMap<Integer, Integer> map;
public MyCalendarThree() {
map = new TreeMap<>();
}
public int book(int start, int end) {
map.put(start, map.getOrDefault(start, 0) + 1);
map.put(end, map.getOrDefault(end, 0) - 1);
int res = 0;
int cnt = 0;
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
cnt += entry.getValue();
if (res < cnt) res = cnt;
}
return res;
}
}
解法二:
线段树求解,效率有较大的提升。
public class MyCalendarThree {
SegmentTree root;
int res;
public MyCalendarThree() {
root = new SegmentTree(0, 1000000000, 0);
res = 0;
}
public int book(int start, int end) {
add(start, end, root);
return res;
}
private void add(int start, int end, SegmentTree root) {
if (root.m != -1) {
if (start >= root.m) add(start, end, root.right);
else if (end <= root.m) add(start, end, root.left);
else {
add(start, root.m, root.left);
add(root.m, end, root.right);
}
return;
}
if (start == root.l && end == root.r) {
root.cnt++;
res = Math.max(res, root.cnt);
}
else if (start == root.l) {
root.m = end;
root.left = new SegmentTree(start, root.m, root.cnt + 1);
root.right = new SegmentTree(root.m, root.r, root.cnt);
res = Math.max(res, root.cnt + 1);
}
else if (end == root.r) {
root.m = start;
root.left = new SegmentTree(root.l, root.m, root.cnt);
root.right = new SegmentTree(root.m, root.r, root.cnt + 1);
res = Math.max(res, root.cnt + 1);
}
else {
root.m = start;
root.left = new SegmentTree(root.l, root.m, root.cnt);
root.right = new SegmentTree(root.m, root.r, root.cnt);
add(start, end, root.right);
}
}
}
class SegmentTree {
int l;
int r;
int m; // m : 分割点,如果尚未分割则为-1。
int cnt;
SegmentTree left;
SegmentTree right;
SegmentTree(int l, int r, int cnt) {
this.l = l;
this.r = r;
this.m = -1;
this.cnt = cnt;
this.left = null;
this.right = null;
}
}
六、Interval List Intersections
问题描述:

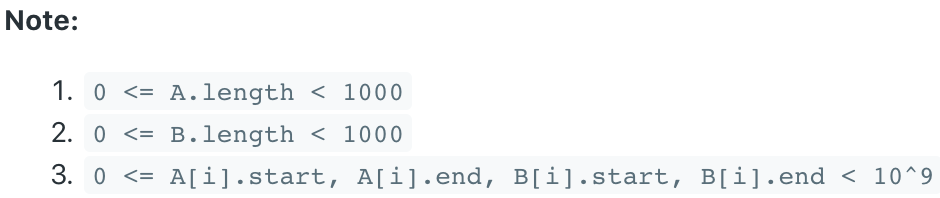
问题求解:
如何快速判断是否相交呢?

public int[][] intervalIntersection(int[][] A, int[][] B) {
List<int[]> res = new ArrayList<>();
int i = 0;
int j = 0;
while (i < A.length && j < B.length) {
int s = Math.max(A[i][0], B[j][0]);
int e = Math.min(A[i][1], B[j][1]);
if (s <= e) res.add(new int[]{s, e});
if (A[i][1] < B[j][1]) i++;
else j++;
}
int[][] rst = new int[res.size()][2];
for (i = 0; i < res.size(); i++) {
rst[i][0] = res.get(i)[0];
rst[i][1] = res.get(i)[1];
}
return rst;
}







