Educational Codeforces Round 73 (Rated for Div. 2)

Stella981
• 阅读 863

传送门

A. 2048 Game

乱搞即可。

Code 
#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 5;
 
int n;
int a[N];
 
void run() {
    cin >> n;
    int cnt = 0, cnt1 = 0;
    for(int i = 1; i <= n; i++) {
        cin >> a[i];
        if(a[i] > 2048) continue;
        if(a[i] == 1) ++cnt1;
        else {
            cnt += a[i] / 2;
        }
    }
    cnt += cnt1 / 2;
    if(cnt >= 1024) cout << "YES" << '\n';
    else cout << "NO" << '\n';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

B. Knights

直接按奇偶分类其实就行，但我写了个$dfs$...

Code 
#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 105;
 
int n;
int a[N][N];
int dx[8] = {-2, -2, -1, -1, 2, 2, 1, 1};
int dy[8] = {-1, 1, -2, 2, -1, 1, -2, 2};
bool chk(int x, int y) {
    return x <= n && x >= 1 && y >= 1 && y <= n && a[x][y] == 0;
}
 
void dfs(int x, int y, int c) {
    a[x][y] = c;
    for(int i = 0; i < 8; i++) {
        int nowx = x + dx[i], nowy = y + dy[i];
        if(chk(nowx, nowy)) dfs(nowx, nowy, 3 - c);
    }
}
 
void run() {
    memset(a, 0, sizeof(a));
    dfs(1, 1, 1);
    for(int i = 1; i <= n; i++) {
        for(int j = 1; j <= n; j++) {
            if(a[i][j] == 1) cout << 'W';
            else cout << 'B';
        }
        cout << '\n';
    }
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    while(cin >> n) run();
    return 0;
}

C. Perfect Team

直接输出就行，但我写了个二分...

Code 
#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e5 + 5;
 
int c, m, x;
 
bool chk(int q) {
    int nc = c - q, nm = m - q;
    return nc >= 0 && nm >= 0 && nc + nm + x >= q;
}
 
void run() {
    cin >> c >> m >> x;
    int ans = min(c, m);
    if(x >= ans) {
        cout << ans << '\n'; return;
    }
    int l = 0, r = 100000002, mid;
    while(l < r) {
        mid = (l + r) >> 1;
        if(chk(mid)) l = mid + 1;
        else r = mid;
    }
    cout << r - 1 << '\n';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

D. Make The Fence Great Again

题意： 给出$n$个数，现在定义一个好的序列为：对于任意相邻的$i,j$，满足$a_i\not ={a_j}$。 现在你可以每次将一个数增加$1$，代价为$b_i$。 问将给出的序列变成好的序列的最小代价为多少。

思路：

  • 注意到一个数最多增加两次，因为如果增加的次数大于$2$的话，就会有空隙，填补那个空隙就行了。
  • 那么定义$dp[i,j]$表示考虑了前$i$个数，最后一个数增加了$j$次的最小代价，直接枚举转移即可。

代码如下：

Code 
#include <bits/stdc++.h>
#define INF 2000000000000000000
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 3e5 + 5;
 
ll dp[N][5];
int n;
int a[N], b[N];
 
void run() {
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> a[i] >> b[i];
    for(int i = 0; i <= n; i++) for(int j = 0; j < 5; j++) dp[i][j] = INF;
    for(int i = 0; i < 5; i++) dp[0][i] = 0;
    for(int i = 1; i <= n; i++) {
        for(int j = 0; j < 4; j++) {
            for(int k = 0; k < 4; k++) {
                if(i == 1 || a[i - 1] + k != a[i] + j) {
                    dp[i][j] = min(dp[i - 1][k] + 1ll * j * b[i], dp[i][j]);
                }
            }
        }
    }
    ll ans = INF;
    for(int i = 0; i < 4; i++) ans = min(ans, dp[n][i]);
    cout << ans << '\n';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

E. Game With String

题意： 给出一个$01$序列，两个人来玩博弈游戏，博弈规则如下：

  • $A$为先手，$B$为后手，给出$a,b,b<a$，$A$能够将$a$个连续的$a$个$0$变为$1$；$B$能够将连续的$b$个$0$变为$1$。
  • 当有一个人无法操作时，则输掉这场游戏。

现给出长度不超过$10^5$的序列，问谁胜谁负。

思路： 感觉很有意思的一道博弈题，跟平时遇到的博弈题不一样。感觉不一样就在于游戏规则对于双方来说都不一样，好像是非平衡博弈？ 首先有一个很重要的观察：

  • 如果存在一段连续的$0$的长度$x$满足：$b\leq x<a$，那么$B$必胜。
简要证明

$B$会比$A$多一次机会。 $A$能搞的$B$也能搞；若出现一个局面，$B$必须用掉这一次机会，那么说明其它位置肯定不存在一段长度大于等于$b$了，自然之后$A$不能再搞了。

那么现在考虑，在什么样的局面下，$B$能够构造出上述观察。 思考可以发现，当存在两段连续$0$的个数都大于等于$2b$时，$B$必然可以构造出这样一段，当然原来就有这么一段就不说了。 发现剩下的情况个数很少，我们直接分类讨论：

  • 当不存在任何一个段长度大于等于$2b$时，显然此时所有合法段的长度都是不小于$a$的（前面的情况已经排除）。那么此时的胜负就根据合法段的奇偶个数。
  • 当仅存在一个时，既然只有一段，直接枚举$A$在该段上的所有选择，看看存不存在必胜状态就行啦。$A$开始必然在这段区间上面选，不然$B$可以随便构造出满足“观察”的段。

代码如下：

Code 
#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int N = 3e5 + 5;
 
char s[N];
int a, b;
 
void A() {
    cout << "YES" << '\n';
}
 
void B() {
    cout << "NO" << '\n';
}
 
void run() {
    vector <int> v;
    cin >> a >> b;
    cin >> s + 1;
    int n = strlen(s + 1);
    int cnt = 0;
    for(int i = 1; i <= n; i++) {
        if(s[i] == '.') ++cnt;
        else {
            if(cnt) {
                v.push_back(cnt);
                cnt = 0;
            }
        }
    }
    if(cnt) v.push_back(cnt); cnt = 0;
    int f = 0;
    for(auto it : v) {
        if(it >= 2 * b) ++cnt;
        if(it >= b && it < a) f = 1;
    }
    if(f || cnt >= 2) {
        B(); return;
    }
    if(cnt == 0) {
        for(auto it : v) {
            if(it >= a) ++cnt;
        }
        if(cnt & 1) A();
        else B();
        return ;
    }
    int mx = *max_element(all(v));
    cnt = 0;
    for(auto it : v) {
        if(it != mx && it >= a) ++cnt;
    }
    for(int l = 1;  l + a - 1 <= mx; l++) {
        int r = l + a - 1;
        int left = l - 1, right = mx - r;
        if(left >= 2 * b || right >= 2 * b) continue;
        if((left >= b && left < a) || (right >= b && right < a)) continue;
        int tmp = cnt + (left >= a) + (right >= a);
        if(tmp % 2 == 0) {
            A(); return;
        }
    }
    B();
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    int q; cin >> q;
    while(q--) run();
    return 0;
}

F. Choose a Square

题意： 二维平面上给出$n$个点，每个点都有个权值。现在要求选择一个正方形，满足其中一根对角线的两顶点在$y=x$这条直线上。 问所选正方形包含了的点的权值和减去边长的最大值。 类似于这样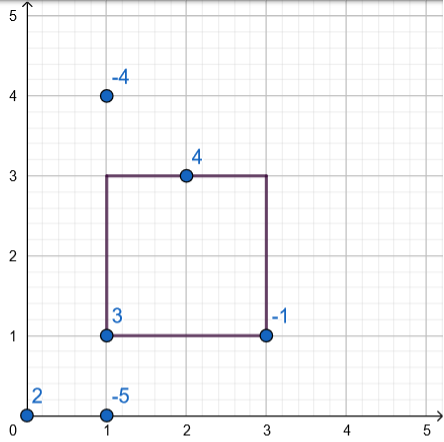： Educational Codeforces Round 73 (Rated for Div. 2) 答案为$4$。

思路：

  • 因为正方形具有对称性，所以我们可以考虑将$y=x$这条直线下方的点对称过去处理，那么我们现在就相当于选择一个等腰直角三角形的区域，类似于这样：

  • 注意到最终三角形的边上一定存在至少一个点，那么也就是说有用的横纵坐标就为这些点的坐标。

  • 直接枚举$x,y$显然复杂度不能承受，考虑当我们枚举$x$时，选择一个最大的$y$，就类似于维护一个区间最大值。

  • 对于一个位置$x=x_0$，显然随着$y$增大包含的点越多，并且对于一个$y=y_0$而言，与$y=x$这条直线所形成的三角形区域是必选的。类似于这样：

  • 所以线段树的做法就很显然了，横坐标直接从后往前枚举，依次加点并且不断在线段树中插入点的信息并更新区间信息，查询的时候就直接查询最大值以及纵坐标即可。

  • 为什么是更新区间最大值？

  • 因为每插入一个点，它会影响在它右上方的点，当选择右上方的点时，它也必然被包含，类似于这样：（所以直接更新在其上方的区间信息即可）

  • 注意一个细节，因为最后还要减去正方形的边长，对于一个点$(x,y)$而言，正方形边长就为$y-x$，减去就是加上$x-y$。因为我们是按照$y$值建立线段树的，初始答案就为$-y$，最后加上枚举的$x$就行了。

最后还要注意特判一下答案为负的情况，可能答案不包含任何点。 详见代码：

Code 
#include <bits/stdc++.h>
#define MP make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define all(x) (x).begin(), (x).end()
//#define Local
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pll;
const int N = 5e5 + 5;
 
int n;
vector <int> v;
pll tr[N << 2];
ll add[N << 2];
 
struct node{
    int x, y, c;
    bool operator < (const node &A) const{
        return x < A.x;
    }
}p[N];
 
void push_up(int o) {
    tr[o] = max(tr[o << 1], tr[o << 1|1]);
}
 
void push_down(int o, int l, int r) {
    if(add[o]) {
        tr[o << 1].fi += add[o];
        tr[o << 1|1].fi += add[o];
        add[o << 1] += add[o];
        add[o << 1|1] += add[o];
        add[o] = 0;
    }
}
 
void build(int o, int l, int r) {
    add[o] = 0;
    if(l == r) {
        tr[o] = MP(-v[l], v[l]);
        return;
    }
    int mid = (l + r) >> 1;
    build(o << 1, l, mid); build(o << 1|1, mid + 1, r);
    push_up(o);
}
 
void update(int o, int l, int r, int x, int c) {
    if(x <= v[l]) {
        tr[o].fi += c;
        add[o] += c;
        return;
    }
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    if(x <= v[mid]) update(o << 1, l, mid, x, c);
    update(o << 1|1, mid + 1, r, x, c);
    push_up(o);
}
 
pll query(int o, int l, int r, int L) {
    if(L > v[r]) return MP(-1000000009, 0);
    if(L <= v[l]) return tr[o];
    push_down(o, l, r);
    int mid = (l + r) >> 1;
    pll ret = max(query(o << 1, l, mid, L), query(o << 1|1, mid + 1, r, L));
    return ret;
}
 
void run() {
    v.clear();
    for(int i = 1; i <= n; i++) {
        int x, y, c; cin >> x >> y >> c;
        if(x > y) swap(x, y);
        p[i] = {x, y, c};
        v.push_back(y);
    }
    sort(all(v));
    v.erase(unique(all(v)), v.end());
    build(1, 0, sz(v) - 1);
    sort(p + 1, p + n + 1);
    p[0].x = -1;
    pll ans = MP(-1000000009, 0);
    int ansx;
    for(int i = n; i >= 1; i--) {
        update(1, 0, sz(v) - 1, p[i].y, p[i].c);
        if(p[i - 1].x != p[i].x) {
            pll ret = query(1, 0, sz(v) - 1, p[i].x);
            ret.fi += p[i].x;
            if(ret > ans) {
                ans = ret;
                ansx = p[i].x;
            }
        }
    }
    if(ans.fi < 0) {
        ans = MP(0, 1000000001), ansx = 1000000001;
    }
    cout << ans.fi << ' ' << ansx << ' ' << ansx << ' ' << ans.se << ' ' << ans.se << '\n';
}
 
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cout << fixed << setprecision(20);
#ifdef Local
    freopen("../input.in", "r", stdin);
    freopen("../output.out", "w", stdout);
#endif
    while(cin >> n) run();
    return 0;
}
ratedtypedeffreopen前端前端
点赞
收藏
评论区
推荐文章
blmius blmius
•
4年前
MySQL:[Err] 1292 - Incorrect datetime value: ‘0000-00-00 00:00:00‘ for column ‘CREATE_TIME‘ at row 1
文章目录问题用navicat导入数据时，报错：原因这是因为当前的MySQL不支持datetime为0的情况。解决修改sql\mode:sql\mode:SQLMode定义了MySQL应支持的SQL语法、数据校验等，这样可以更容易地在不同的环境中使用MySQL。全局s
7320
0
0
美凌格栋栋酱 美凌格栋栋酱
•
9个月前
Oracle 分组与拼接字符串同时使用
SELECTT.,ROWNUMIDFROM(SELECTT.EMPLID,T.NAME,T.BU,T.REALDEPART,T.FORMATDATE,SUM(T.S0)S0,MAX(UPDATETIME)CREATETIME,LISTAGG(TOCHAR(
4008
0
0
Wesley13 Wesley13
•
4年前
MySQL部分从库上面因为大量的临时表tmp_table造成慢查询
背景描述Time:20190124T00:08:14.70572408:00User@Host:@Id:Schema:sentrymetaLast_errno:0Killed:0Query_time:0.315758Lock_
3793
0
0
helloworld_34035044 helloworld_34035044
•
3年前
皕杰报表之UUID
​在我们用皕杰报表工具设计填报报表时，如何在新增行里自动增加id呢？能新增整数排序id吗？目前可以在新增行里自动增加id，但只能用uuid函数增加UUID编码，不能新增整数排序id。uuid函数说明：获取一个UUID，可以在填报表中用来创建数据ID语法：uuid()或uuid(sep)参数说明：sep布尔值，生成的uuid中是否包含分隔符''，缺省为
3297
0
0
Jacquelyn38 Jacquelyn38
•
4年前
2020年前端实用代码段，为你的工作保驾护航
有空的时候，自己总结了几个代码段，在开发中也经常使用，谢谢。1、使用解构获取json数据let jsonData  id: 1,status: "OK",data: 'a', 'b';let  id, status, data: number   jsonData;console.log(id, status, number )
3177
0
0
Stella981 Stella981
•
4年前
AndroidStudio封装SDK的那些事
<divclass"markdown\_views"<!flowchart箭头图标勿删<svgxmlns"http://www.w3.org/2000/svg"style"display:none;"<pathstrokelinecap"round"d"M5,00,2.55,5z"id"raphael
1548
0
0
Wesley13 Wesley13
•
4年前
mysql设置时区
mysql设置时区mysql\_query("SETtime\_zone'8:00'")ordie('时区设置失败，请联系管理员！');中国在东8区所以加8方法二：selectcount(user\_id)asdevice,CONVERT\_TZ(FROM\_UNIXTIME(reg\_time),'08:00','0
3152
0
0
Wesley13 Wesley13
•
4年前
00：Java简单了解
浅谈Java之概述Java是SUN(StanfordUniversityNetwork)，斯坦福大学网络公司)1995年推出的一门高级编程语言。Java是一种面向Internet的编程语言。随着Java技术在web方面的不断成熟，已经成为Web应用程序的首选开发语言。Java是简单易学，完全面向对象，安全可靠，与平台无关的编程语言。
2239
0
0
Stella981 Stella981
•
4年前
Django中Admin中的一些参数配置
设置在列表中显示的字段，id为django模型默认的主键list_display('id','name','sex','profession','email','qq','phone','status','create_time')设置在列表可编辑字段list_editable
2966
0
0
Python进阶者 Python进阶者
•
1年前
Excel中这日期老是出来00：00：00，怎么用Pandas把这个去除
大家好，我是皮皮。一、前言前几天在Python白银交流群【上海新年人】问了一个Pandas数据筛选的问题。问题如下：这日期老是出来00：00：00，怎么把这个去除。二、实现过程后来【论草莓如何成为冻干莓】给了一个思路和代码如下：pd.toexcel之前把这
2585
0
0
Stella981
Stella981
Lv1
接天莲叶无穷碧，映日荷花别样红。
文章
1.7w
粉丝
45
获赞
30
热门文章
OpenVPN下载、安装、配置及使用详解
GitHub神器，一个可以白嫖全网无损音乐的神器
OpenWrt 路由器过滤广告的N种方法
Python—执行系统命令的四种方法（os.system、os.popen、commands、subprocess）
SS端加密以及obfs混淆