在这篇文章中，我们将在Python中从头开始了解用于构建具有各种层神经网络（完全连接，卷积等）的小型库中的机器学习和代码。最终，我们将能够写出如下内容：

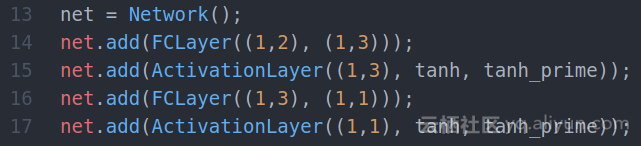
假设你对神经网络已经有一定的了解，这篇文章的目的不是解释为什么构建这些模型，而是要说明如何正确实现。

逐层

我们这里需要牢记整个框架：

1.     将数据输入神经网络

2.     在得出输出之前，数据从一层流向下一层

3.     一旦得到输出，就可以计算出一个标量误差。

4.     最后，可以通过相对于参数本身减去误差的导数来调整给定参数（权重或偏差）。

5.     遍历整个过程。

最重要的一步是第四步。 我们希望能够拥有任意数量的层，以及任何类型的层。 但是如果修改/添加/删除网络中的一个层，网络的输出将会改变，误差也将改变，误差相对于参数的导数也将改变。无论网络架构如何、激活函数如何、损失如何，都必须要能够计算导数。

为了实现这一点，我们必须分别实现每一层。

每个层应该实现什么

我们可能构建的每一层（完全连接，卷积，最大化，丢失等）至少有两个共同点：输入和输出数据。

现在重要的一部分

假设给出一个层*相对于其输出（∂E/∂Y）误差的导数，那么它必须能够提供相对于其输入（∂E/∂X*）误差的导数。

 

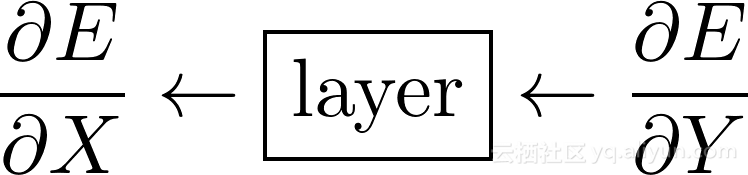
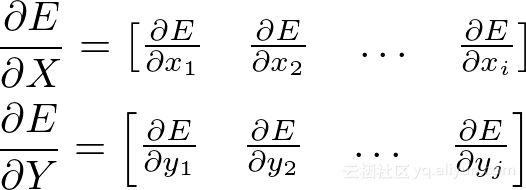
我们可以使用链规则轻松计算∂E/∂X的元素：

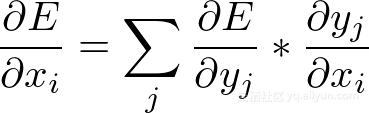
*为什么是∂E/∂X*？

对于每一层，我们需要相对于其输入的误差导数，因为它将是相对于前一层输出的误差导数。这非常重要，这是理解反向传播的关键！在这之后，我们将能够立即从头开始编写深度卷积神经网络！

花样图解

基本上，对于前向传播，我们将输入数据提供给第一层，然后每层的输出成为下一层的输入，直到到达网络的末端。

对于反向传播，我们只是简单使用链规则来获得需要的导数。这就是为什么每一层必须提供其输出相对于其输入的导数。

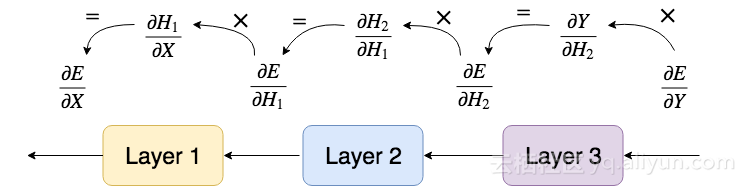
这可能看起来很抽象，但是当我们将其应用于特定类型的层时，它将变得非常清楚。现在是编写第一个python类的好时机。

抽象基类：****Layer

所有其它层将继承的抽象类Layer会处理简单属性，这些属性是输入，输出以及前向和反向方法。

from abc import abstractmethod
# Base class
class Layer:
    def __init__(self):
        self.input = None;
        self.output = None;
        self.input_shape = None;
        self.output_shape = None;
    # computes the output Y of a layer for a given input X
    @abstractmethod
    def forward_propagation(self, input):
        raise NotImplementedError

    # computes dE/dX for a given dE/dY (and update parameters if any)
    @abstractmethod
    def backward_propagation(self, output_error, learning_rate):
        raise NotImplementedError

正如你所看到的，在back_propagation函数中，有一个我没有提到的参数，它是learning_rate。 此参数应该类似于更新策略或者在Keras中调用它的优化器，为了简单起见，我们只是通过学习率并使用梯度下降更新我们的参数。

全连接层

现在先定义并实现第一种类型的网络层：全连接层或FC层。FC层是最基本的网络层，因为每个输入神经元都连接到每个输出神经元。

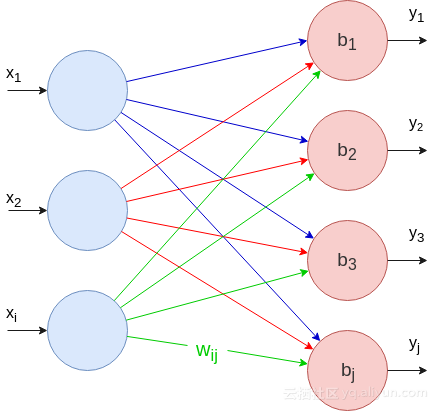
前向传播

每个输出神经元的值由下式计算：

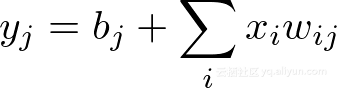
使用矩阵，可以使用点积来计算每一个输出神经元的值：

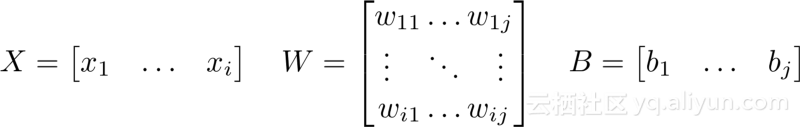
当完成前向传播之后，现在开始做反向传播。

反向传播

正如我们所说，假设我们有一个矩阵，其中包含与该层输出相关的误差导数（∂E/∂Y）。 我们需要 ：

1.关于参数的误差导数（∂E/∂W，∂E/∂B）

2.关于输入的误差导数（∂E/∂X）

首先计算∂E/∂W，该矩阵应与W本身的大小相同：对于ixj，其中i是输入神经元的数量，j是输出神经元的数量。每个权重都需要一个梯度：

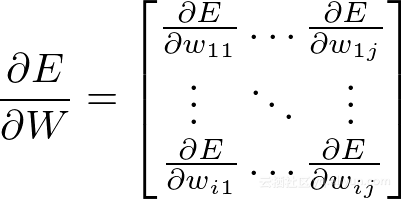
使用前面提到的链规则，可以写出：

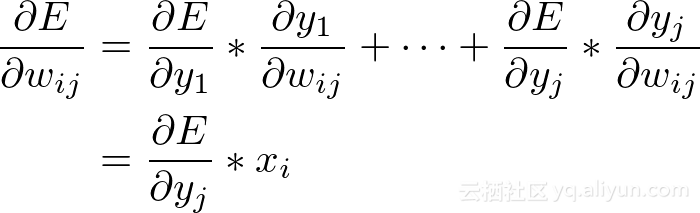
那么：

这就是更新权重的第一个公式！现在开始计算∂E/∂B：

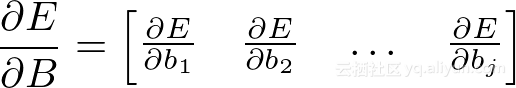
同样，∂E/∂B需要与B本身具有相同的大小，每个偏差一个梯度。 我们可以再次使用链规则：

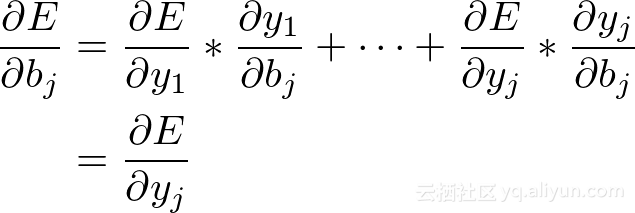
得出结论：

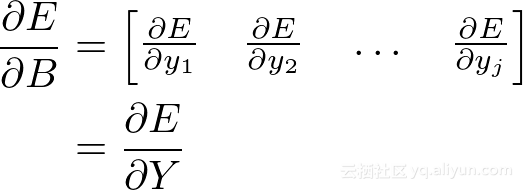
现在已经得到∂E/∂W和∂E/∂B，我们留下∂***E/∂X**这是*非常重要的，因为它将“作用”为之前层的∂E/∂Y。

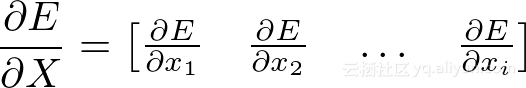
再次使用链规则：

最后，我们可以写出整个矩阵：

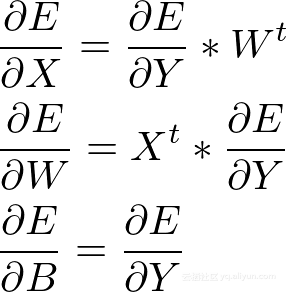
编码全连接层

现在我们可以用Python编写实现：

from layer import Layer
import numpy as np

# inherit from base class Layer
class FCLayer(Layer):
    # input_shape = (1,i)   i the number of input neurons
    # output_shape = (1,j)  j the number of output neurons
    def __init__(self, input_shape, output_shape):
        self.input_shape = input_shape;
        self.output_shape = output_shape;
        self.weights = np.random.rand(input_shape[1], output_shape[1]) - 0.5;
        self.bias = np.random.rand(1, output_shape[1]) - 0.5;

    # returns output for a given input
    def forward_propagation(self, input):
        self.input = input;
        self.output = np.dot(self.input, self.weights) + self.bias;
        return self.output;

    # computes dE/dW, dE/dB for a given output_error=dE/dY. Returns input_error=dE/dX.
    def backward_propagation(self, output_error, learning_rate):
        input_error = np.dot(output_error, self.weights.T);
        dWeights = np.dot(self.input.T, output_error);
        # dBias = output_error
        
        # update parameters
        self.weights -= learning_rate * dWeights;
        self.bias -= learning_rate * output_error;
        return input_error;

激活层

到目前为止所做的计算都完全是线性的。用这种模型学习是没有希望的，需要通过将非线性函数应用于某些层的输出来为模型添加非线性。

现在我们需要为这种新类型的层（激活层）重做整个过程！

不用担心，因为此时没有可学习的参数，过程会快点，只需要计算∂E/∂X。

我们将f和f'分别称为激活函数及其导数。

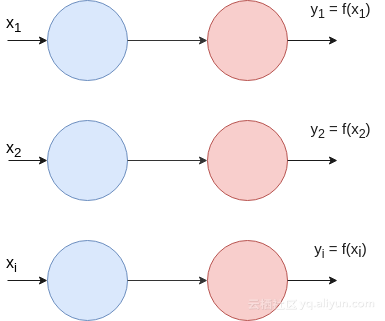
前向传播

正如将看到的，它非常简单。对于给定的输入X，输出是关于每个X元素的激活函数，这意味着输入和输出具有相同的大小。

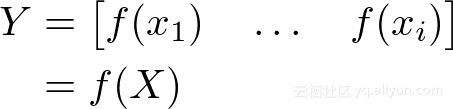
反向传播

给出∂E/∂Y，需要计算∂E/∂X

注意，这里我们使用两个矩阵之间的每个元素乘法（而在上面的公式中，它是一个点积）

编码实现激活层

激活层的代码非常简单：

from layer import Layer
# inherit from base class Layer
class ActivationLayer(Layer):
    # input_shape = (1,i)   i the number of input neurons
    def __init__(self, input_shape, activation, activation_prime):
        self.input_shape = input_shape;
        self.output_shape = input_shape;
        self.activation = activation;
        self.activation_prime = activation_prime;

    # returns the activated input
    def forward_propagation(self, input):
        self.input = input;
        self.output = self.activation(self.input);
        return self.output;

    # Returns input_error=dE/dX for a given output_error=dE/dY.
    # learning_rate is not used because there is no "learnable" parameters.
    def backward_propagation(self, output_error, learning_rate):
        return self.activation_prime(self.input) * output_error;

可以在单独的文件中编写一些激活函数以及它们的导数，稍后将使用它们构建ActivationLayer：

import numpy as np
# activation function and its derivative
def tanh(x):
    return np.tanh(x);

def tanh_prime(x):
    return 1-np.tanh(x)**2;

损失函数

到目前为止，对于给定的层，我们假设给出了∂E/∂Y（由下一层给出）。但是最后一层怎么得到∂E/∂Y？我们通过简单地手动给出最后一层的∂E/∂Y，它取决于我们如何定义误差。

网络的误差由自己定义，该误差衡量网络对给定输入数据的好坏程度。有许多方法可以定义误差，其中一种最常见的叫做MSE - Mean Squared Error：

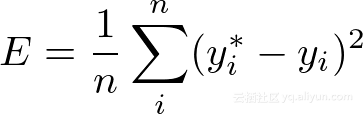
其中y *和y分别表示期望的输出和实际输出。你可以将损失视为最后一层，它将所有输出神经元吸收并将它们压成一个神经元。与其他每一层一样，需要定义∂E/∂Y。除了现在，我们终于得到E！

以下是两个python函数，可以将它们放在一个单独的文件中，将在构建网络时使用。

import numpy as np

# loss function and its derivative
def mse(y_true, y_pred):
    return np.mean(np.power(y_true-y_pred, 2));

def mse_prime(y_true, y_pred):
    return 2*(y_pred-y_true)/y_true.size;

网络类

到现在几乎完成了！我们将构建一个Network类来创建神经网络，非常容易，类似于第一张图片！

我注释了代码的每一部分，如果你掌握了前面的步骤，那么理解它应该不会太复杂。

from layer import Layer

class Network:
    def __init__(self):
        self.layers = [];
        self.loss = None;
        self.loss_prime = None;

    # add layer to network
    def add(self, layer):
        self.layers.append(layer);

    # set loss to use
    def use(self, loss, loss_prime):
        self.loss = loss;
        self.loss_prime = loss_prime;

    # predict output for given input
    def predict(self, input):
        # sample dimension first
        samples = len(input);
        result = [];

        # run network over all samples
        for i in range(samples):
            # forward propagation
            output = input[i];
            for layer in self.layers:
                # output of layer l is input of layer l+1
                output = layer.forward_propagation(output);
            result.append(output);

        return result;

    # train the network
    def fit(self, x_train, y_train, epochs, learning_rate):
        # sample dimension first
        samples = len(x_train);

        # training loop
        for i in range(epochs):
            err = 0;
            for j in range(samples):
                # forward propagation
                output = x_train[j];
                for layer in self.layers:
                    output = layer.forward_propagation(output);

                # compute loss (for display purpose only)
                err += self.loss(y_train[j], output);

                # backward propagation
                error = self.loss_prime(y_train[j], output);
                # loop from end of network to beginning
                for layer in reversed(self.layers):
                    # backpropagate dE
                    error = layer.backward_propagation(error, learning_rate);

            # calculate average error on all samples
            err /= samples;
            print('epoch %d/%d   error=%f' % (i+1,epochs,err));

构建一个神经网络

最后！我们可以使用我们的类来创建一个包含任意数量层的神经网络！为了简单起见，我将向你展示如何构建......一个XOR。

from network import Network
from fc_layer import FCLayer
from activation_layer import ActivationLayer
from losses import *
from activations import *
import numpy as np

# training data
x_train = np.array([[[0,0]], [[0,1]], [[1,0]], [[1,1]]]);
y_train = np.array([[[0]], [[1]], [[1]], [[0]]]);

# network
net = Network();
net.add(FCLayer((1,2), (1,3)));
net.add(ActivationLayer((1,3), tanh, tanh_prime));
net.add(FCLayer((1,3), (1,1)));
net.add(ActivationLayer((1,1), tanh, tanh_prime));

# train
net.use(mse, mse_prime);
net.fit(x_train, y_train, epochs=1000, learning_rate=0.1);

# test
out = net.predict(x_train);
print(out);

同样，我认为不需要强调很多事情，只需要仔细训练数据，应该能够先获得样本维度。例如，对于xor问题，样式应为（4,1,2）。

结果

$ python xor.py epoch 1/1000 error=0.322980 epoch 2/1000 error=0.311174 epoch 3/1000 error=0.307195 ... epoch 998/1000 error=0.000243 epoch 999/1000 error=0.000242 epoch 1000/1000 error=0.000242 [array([[ 0.00077435]]), array([[ 0.97760742]]), array([[ 0.97847793]]), array([[-0.00131305]])]

卷积层

这篇文章开始很长，所以我不会描述实现卷积层的所有步骤。但是，这是我做的一个实现：

from layer import Layer
from scipy import signal
import numpy as np

# inherit from base class Layer
# This convolutional layer is always with stride 1
class ConvLayer(Layer):
    # input_shape = (i,j,d)
    # kernel_shape = (m,n)
    # layer_depth = output depth
    def __init__(self, input_shape, kernel_shape, layer_depth):
        self.input_shape = input_shape;
        self.input_depth = input_shape[2];
        self.kernel_shape = kernel_shape;
        self.layer_depth = layer_depth;
        self.output_shape = (input_shape[0]-kernel_shape[0]+1, input_shape[1]-kernel_shape[1]+1, layer_depth);
        self.weights = np.random.rand(kernel_shape[0], kernel_shape[1], self.input_depth, layer_depth) - 0.5;
        self.bias = np.random.rand(layer_depth) - 0.5;

    # returns output for a given input
    def forward_propagation(self, input):
        self.input = input;
        self.output = np.zeros(self.output_shape);

        for k in range(self.layer_depth):
            for d in range(self.input_depth):
                self.output[:,:,k] += signal.correlate2d(self.input[:,:,d], self.weights[:,:,d,k], 'valid') + self.bias[k];

        return self.output;

    # computes dE/dW, dE/dB for a given output_error=dE/dY. Returns input_error=dE/dX.
    def backward_propagation(self, output_error, learning_rate):
        in_error = np.zeros(self.input_shape);
        dWeights = np.zeros((self.kernel_shape[0], self.kernel_shape[1], self.input_depth, self.layer_depth));
        dBias = np.zeros(self.layer_depth);

        for k in range(self.layer_depth):
            for d in range(self.input_depth):
                in_error[:,:,d] += signal.convolve2d(output_error[:,:,k], self.weights[:,:,d,k], 'full');
                dWeights[:,:,d,k] = signal.correlate2d(self.input[:,:,d], output_error[:,:,k], 'valid');
            dBias[k] = self.layer_depth * np.sum(output_error[:,:,k]);

        self.weights -= learning_rate*dWeights;
        self.bias -= learning_rate*dBias;
        return in_error;

它背后的数学实际上并不复杂！这是一篇很好的文章，你可以找到∂E/∂W，∂E/∂B和∂E/∂X的解释和计算。

如果你想验证你的理解是否正确，请尝试自己实现一些网络层，如MaxPooling，Flatten或Dropout

GitHub库

你可以在GitHub库中找到用于该文章的完整代码。

原文链接