前面我们介绍了三种数据结构,第一种数组主要用作数据存储,但是后面的两种栈和队列我们说主要作为程序功能实现的辅助工具,其中在介绍栈时我们知道栈可以用来做单词逆序,匹配关键字符等等,那它还有别的什么功能吗?以及数据结构与本篇博客的主题前缀、中缀、后缀表达式有什么关系呢?
1、人如何解析算术表达式
如何解析算术表达式?或者换种说法,遇到某个算术表达式,我们是如何计算的:
①、求值 3+4-5
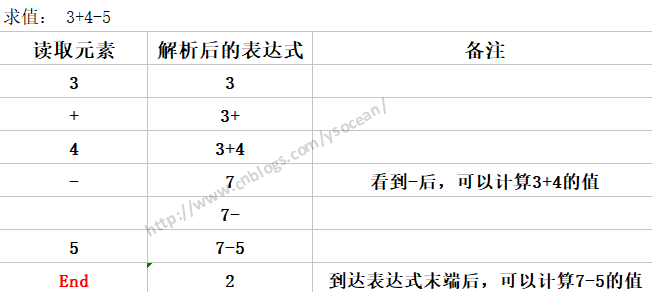
这个表达式,我们在看到3+4后都不能直接计算3+4的值,知道看到4后面的 - 号,因为减号的优先级和前面的加号一样,所以可以计算3+4的值了,如果4后面是 * 或者 /,那么就要在乘除过后才能做加法操作,比如:
②、求值 3+4*5
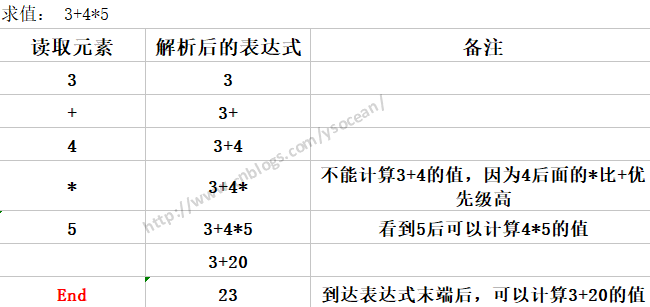
这个不能先求3+4的值,因为4后面的*运算级别比前面的+高。通过这两个表达式的说明,我们可以总结解析表达式的时候遵循的几条规则:
①、从左到右读取算式。
②、已经读到了可以计算值的两个操作数和一个操作符时,可以计算,并用计算结果代替那两个操作数和一个操作符。
③、继续这个过程,从左到右,能算就算,直到表达式的结尾。
2、计算机如何解析算术表达式
对于前面的表达式 3+4-5,我们人是有思维能力的,能根据操作符的位置,以及操作符的优先级别能算出该表达式的结果。但是计算机怎么算?
计算机必须要向前(从左到右)来读取操作数和操作符,等到读取足够的信息来执行一个运算时,找到两个操作数和一个操作符进行运算,有时候如果后面是更高级别的操作符或者括号时,就必须推迟运算,必须要解析到后面级别高的运算,然后回头来执行前面的运算。我们发现这个过程是极其繁琐的,而计算机是一个机器,只认识高低电平,想要完成一个简单表达式的计算,我们可能要设计出很复杂的逻辑电路来控制计算过程,那更不用说很复杂的算术表达式,所以这样来解析算术表达式是不合理的,那么我们应该采取什么办法呢?
请大家先看看什么是前缀表达式,中缀表达式,后缀表达式:这三种表达式其实就是算术表达式的三种写法,以 3+4-5为例
①、前缀表达式:操作符在操作数的前面,比如 +-543
②、中缀表达式:操作符在操作数的中间,这也是人类最容易识别的算术表达式 3+4-5
③、后缀表达式:操作符在操作数的后面,比如 34+5-
上面我们讲的人是如何解析算术表达式的,也就是解析中缀表达式,这是人最容易识别的,但是计算机不容易识别,计算机容易识别的是前缀表达式和后缀表达式,将中缀表达式转换为前缀表达式或者后缀表达式之后,计算机能很快计算出表达式的值,那么中缀表达式是如何转换为前缀表达式和后缀表达式,以及计算机是如何解析前缀表达式和后缀表达式来得到结果的呢?
3、后缀表达式
后缀表达式,指的是不包含括号,运算符放在两个运算对象的后面,所有的计算按运算符出现的顺序,严格从左向右进行(不再考虑运算符的优先规则)。
由于后缀表达式的运算符在两个操作数的后面,那么计算机在解析后缀表达式的时候,只需要从左向右扫描,也就是只需要向前扫描,而不用回头扫描,遇到运算符就将运算符放在前面两个操作符的中间(这里先不考虑乘方类似的单目运算),一直运算到最右边的运算符,那么就得出运算结果了。既然后缀表达式这么好,那么问题来了:
①、如何将中缀表达式转换为后缀表达式?
对于这个问题,转换的规则如下:
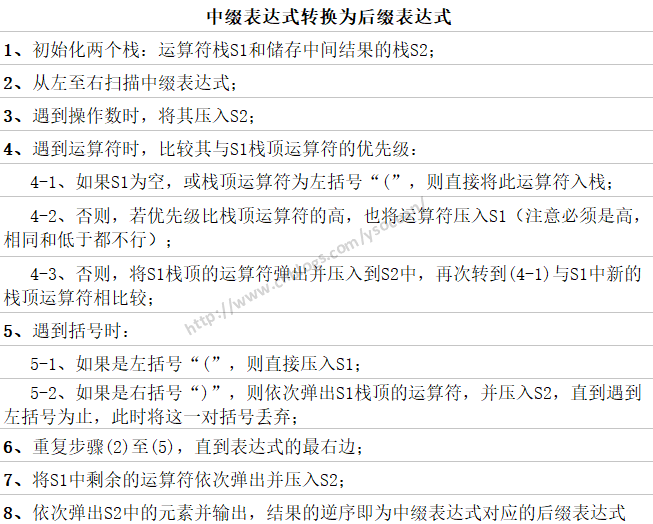
一、先自定义一个栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
package com.ys.poland;
public class MyCharStack {
private char``[] array;
private int maxSize;
private int top;
public MyCharStack(``int size){
this``.maxSize = size;
array = new char``[size];
top = -``1``;
}
//压入数据
public void push(``char value){
if``(top < maxSize-``1``){
array[++top] = value;
}
}
//弹出栈顶数据
public char pop(){
return array[top--];
}
//访问栈顶数据
public char peek(){
return array[top];
}
//查看指定位置的元素
public char peekN(``int n){
return array[n];
}
//为了便于后面分解展示栈中的内容,我们增加了一个遍历栈的方法(实际上栈只能访问栈顶元素的)
public void displayStack(){
System.out.print(``"Stack(bottom-->top):"``);
for``(``int i = 0 ; i < top+``1``; i++){
System.out.print(peekN(i));
System.out.print(``' '``);
}
System.out.println(``""``);
}
//判断栈是否为空
public boolean isEmpty(){
return (top == -``1``);
}
//判断栈是否满了
public boolean isFull(){
return (top == maxSize-``1``);
}
}
二、前缀表达式转换为后缀表达式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
package com.ys.poland;
public class InfixToSuffix {
private MyCharStack s1;``//定义运算符栈
private MyCharStack s2;``//定义存储结果栈
private String input;
//默认构造方法,参数为输入的中缀表达式
public InfixToSuffix(String in){
input = in;
s1 = new MyCharStack(input.length());
s2 = new MyCharStack(input.length());
}
//中缀表达式转换为后缀表达式,将结果存储在栈中返回,逆序显示即后缀表达式
public MyCharStack doTrans(){
for``(``int j = 0 ; j < input.length() ; j++){
System.out.print(``"s1栈元素为:"``);
s1.displayStack();
System.out.print(``"s2栈元素为:"``);
s2.displayStack();
char ch = input.charAt(j);
System.out.println(``"当前解析的字符:"``+ch);
switch (ch) {
case '+'``:
case '-'``:
gotOper(ch,``1``);
break``;
case '*'``:
case '/'``:
gotOper(ch,``2``);
break``;
case '('``:
s1.push(ch);``//如果当前字符是'(',则将其入栈
break``;
case ')'``:
gotParen(ch);
break``;
default``:
//1、如果当前解析的字符是操作数,则直接压入s2
//2、
s2.push(ch);
break``;
}``//end switch
}``//end for
while``(!s1.isEmpty()){
s2.push(s1.pop());
}
return s2;
}
public void gotOper(``char opThis,``int prec1){
while``(!s1.isEmpty()){
char opTop = s1.pop();
if``(opTop == '('``){``//如果栈顶是'(',直接将操作符压入s1
s1.push(opTop);
break``;
}``else``{
int prec2;
if``(opTop == '+' || opTop == '-'``){
prec2 = 1``;
}``else``{
prec2 = 2``;
}
if``(prec2 < prec1){``//如果当前运算符比s1栈顶运算符优先级高,则将运算符压入s1
s1.push(opTop);
break``;
}``else``{``//如果当前运算符与栈顶运算符相同或者小于优先级别,那么将S1栈顶的运算符弹出并压入到S2中
//并且要再次再次转到while循环中与 s1 中新的栈顶运算符相比较;
s2.push(opTop);
}
}
}``//end while
//如果s1为空,则直接将当前解析的运算符压入s1
s1.push(opThis);
}
//当前字符是 ')' 时,如果栈顶是'(',则将这一对括号丢弃,否则依次弹出s1栈顶的字符,压入s2,直到遇到'('
public void gotParen(``char ch){
while``(!s1.isEmpty()){
char chx = s1.pop();
if``(chx == '('``){
break``;
}``else``{
s2.push(chx);
}
}
}
}
三、测试
1
2
3
4
5
6
7
8
9
10
[@Test](https://my.oschina.net/azibug)
public void testInfixToSuffix(){
String input;
System.out.println(``"Enter infix:"``);
Scanner scanner = new Scanner(System.in);
input = scanner.nextLine();
InfixToSuffix in = new InfixToSuffix(input);
MyCharStack my = in.doTrans();
my.displayStack();
}
四、结果

五、分析
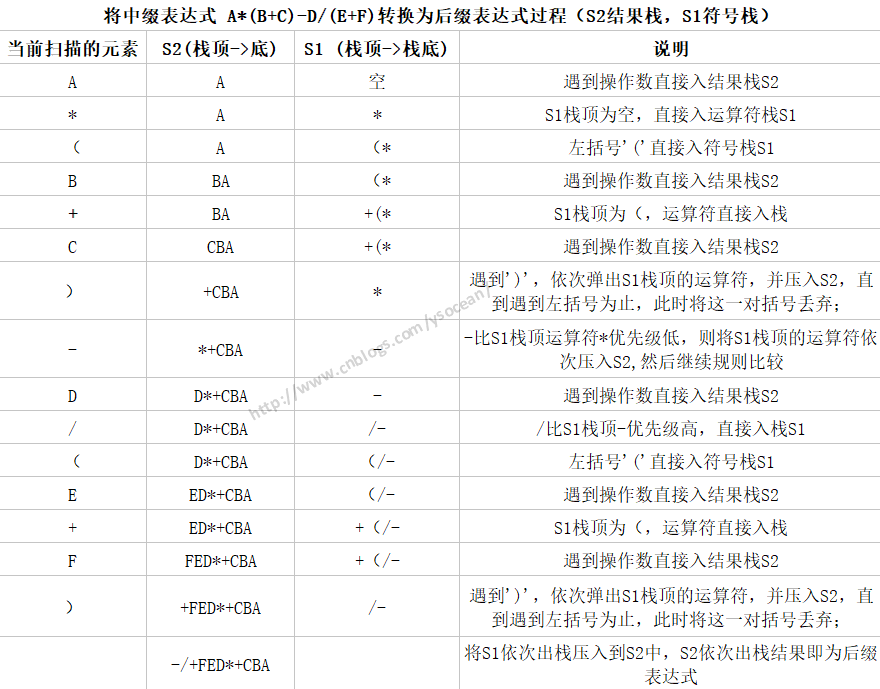
②、计算机如何实现后缀表达式的运算?

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
package com.ys.poland;
public class CalSuffix {
private MyIntStack stack;
private String input;
public CalSuffix(String input){
this``.input = input;
stack = new MyIntStack(input.length());
}
public int doCalc(){
int num1,num2,result;
for``(``int i = 0 ; i < input.length() ; i++){
char c = input.charAt(i);
if``(c >= '0' && c <= '9'``){
stack.push((``int``)(c-``'0'``));``//如果是数字,直接压入栈中
}``else``{
num2 = stack.pop();``//注意先出来的为第二个操作数
num1 = stack.pop();
switch (c) {
case '+'``:
result = num1+num2;
break``;
case '-'``:
result = num1-num2;
break``;
case '*'``:
result = num1*num2;
break``;
case '/'``:
result = num1/num2;
break``;
default``:
result = 0``;
break``;
}``//end switch
stack.push(result);
}``//end else
}``//end for
result = stack.pop();
return result;
}
public static void main(String[] args) {
//中缀表达式:1*(2+3)-5/(2+3) = 4
//后缀表达式:123+*123+/-
CalSuffix cs = new CalSuffix(``"123+*523+/-"``);
System.out.println(cs.doCalc()); //4
}
}
4、前缀表达式
前缀表达式,指的是不包含括号,运算符放在两个运算对象的前面,严格从右向左进行(不再考虑运算符的优先规则),所有的计算按运算符出现的顺序。
注意:后缀表达式是从左向右解析,而前缀表达式是从右向左解析。
①、如何将中缀表达式转换为前缀表达式?

②、计算机如何实现前缀表达式的运算?














