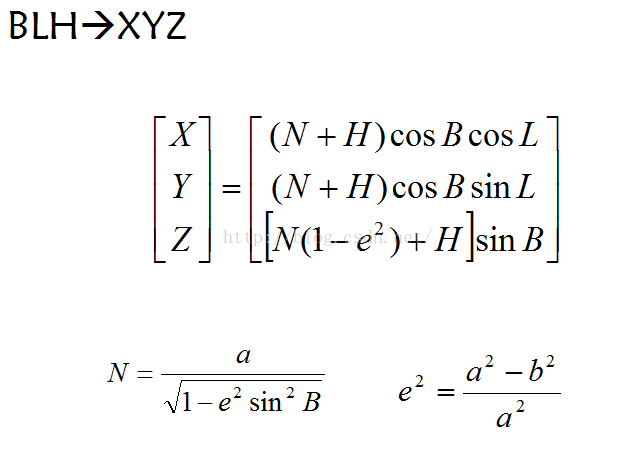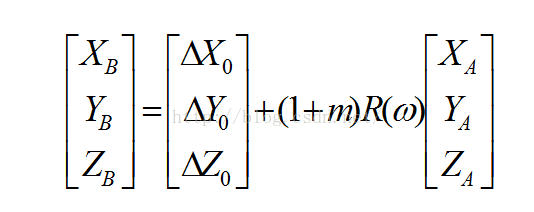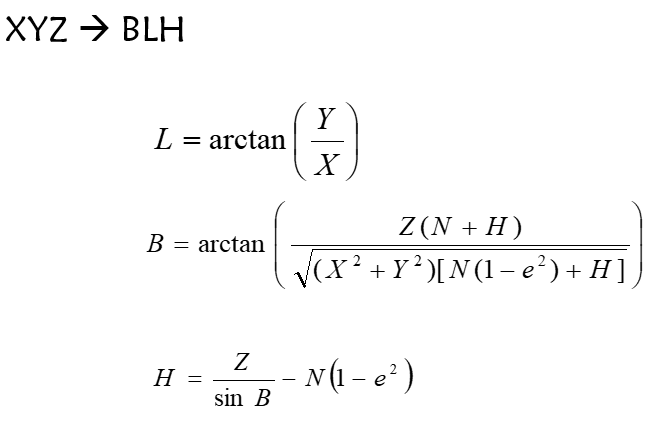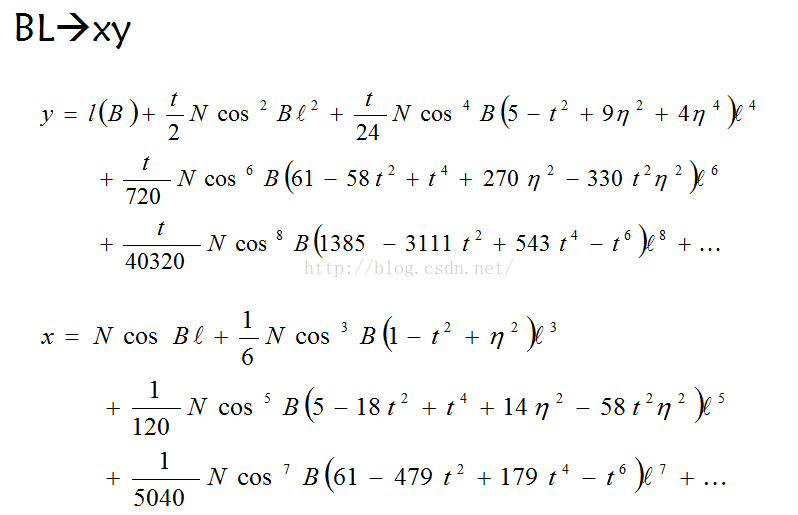80、54、84坐标系七参数转换算法

一、为什么要进行坐标转换

我们所在地球是一个不规则的椭球，地表凹凸不平，地底密度不均，因此很难用一个简单模型来概括。国际上根据建模坐标系的原点不同分为参心坐标系和地心坐标系，其中参心坐标系是指参考椭球的几何中心坐标基准，地心，通常分为：参心空间直角坐标系（以x，y，z为其坐标元素）和参心大地坐标系（以B，L，H为其坐标元素），比如我国的北京54坐标系和西安80坐标系；坐标系是用地球质心作为原点，通常分为地心空间直角坐标系(以x，y，z为其坐标元素)和地心大地坐标系(以B，L，H为其坐标元素)，比如GPS采用的WGS84坐标系。

除了原点以外，任何一个椭球的模型还会有长轴、短轴和扁率三个参数，我整理了下54,80,84三个坐标的椭球模型如下表:

坐标系

长轴（单位：米）

短轴（单位：米）

扁率

北京54坐标系

6378245

6356863

1/298.3

西安80坐标系

6378140

6356755

1/298.25722101

WGS84坐标系

6378137

6356752.314

1/298.25722356

所以，我们可见这三个坐标系是原点不一，椭球模型不一的坐标系，就如同三个达芬奇的鸡蛋，虽然都是椭球状，但是形状还是不一样的。所以如果直接做两个坐标系之间的转换是明显不行的。

那么有没有办法进行转换呢？答案是肯定的。在数学上，任何两个空间直角坐标系都可以通过七个参数，即XYZ三个轴的平移，绕XYZ三个轴的旋转角以及两个坐标系的大小比例因子的转换后重叠在一起。因此，我们在做着三个坐标系的转换基本思路就是在空间直角坐标系里，通过七参数的偏移校正，实现坐标系之间参数的转换。

二、怎样坐标转换

好了，那我们如何转换呢。首先，我再区分一下地理上的空间直角坐标系、大地坐标系和平面坐标系的区别。

空间直角坐标系和数学的空间直角坐标系基本相同，是以一个点为原点，三个互相垂直的直线作为三个轴延伸出来一个坐标系，通常表示为（x,y,z）；

大地坐标系是其地面上一点的大地经度L为大地起始子午面与该点所在的子午面所构成的二面角，由起始子午面起算，向东为正，称为东经（0~~180），向西为负，称为西经（0~~180）；大地纬度B是经过该点作椭球面的法线与赤道面的夹角，由赤道面起算，向北为正，称为北纬（0~~90），向南为负，称为南纬（0~~90）；大地高H是地面点沿椭球的法线到椭球面的距离，通常表示为（B,L,H）；

平面坐标系主要是我国测绘领域里使用的坐标系，属于参心大地坐标系，有一个坐标原点（54位原苏联的普尔科沃，80位我们陕西省泾阳县永乐镇），Z轴平行于地球质心指向地极原点方向，大地起始子午面平行于格林尼治平均天文台子午面，X轴在大地起始子午面内与Z轴垂直指向经度0方向，Y轴与Z、X轴成右手坐标系。因为大地高程以1956年青岛验潮站求出的黄海平均水面为基准，一般情况默认为0，所以通常表示为（X,Y）。

下面我以一个例子说明下如何进行WGS84坐标系转西安80坐标系

WGS84坐标系是大地坐标系，首先要转换到空间直角坐标系，公式如图所示：

80、54、84坐标系七参数转换算法

其中a,b是WGS84椭球长短轴。代码为：

//第一步转换，大地坐标系换换成空间直角坐标系
private void BLHtoXYZ(double B, double L, double H, double aAxis, double bAxis) {
double dblD2R = Math.PI / 180;
double e1 = Math.sqrt(Math.pow(aAxis, 2) - Math.pow(bAxis, 2)) / aAxis;
double N = aAxis / Math.sqrt(1.0 - Math.pow(e1, 2) * Math.pow(Math.sin(B * dblD2R), 2));
targetX = (N + H) * Math.cos(B * dblD2R) * Math.cos(L * dblD2R);
targetY = (N + H) * Math.cos(B * dblD2R) * Math.sin(L * dblD2R);
targetZ = (N * (1.0 - Math.pow(e1, 2)) + H) * Math.sin(B * dblD2R);
}

第二步是进行空间直角坐标系里七参数转换，公式如图：

80、54、84坐标系七参数转换算法

其中△X，△Y，△Z是坐标平移量，R（ω）是旋转矩阵，（1+m）是比例因子，代码如下：

//第二步转换，空间直角坐标系里七参数转换
Ex = transParaSeven.m_dbXRotate / 180 * Math.PI;
Ey = transParaSeven.m_dbYRotate / 180 * Math.PI;
Ez = transParaSeven.m_dbZRotate / 180 * Math.PI;
double newX = transParaSeven.m_dbXOffset + transParaSeven.m_dbScale * targetX + targetY * Ez - targetZ * Ey + targetX;
double newY = transParaSeven.m_dbYOffset + transParaSeven.m_dbScale * targetY - targetX * Ez + targetZ * Ex + targetY;
double newZ = transParaSeven.m_dbZOffset + transParaSeven.m_dbScale * targetZ + targetX * Ey - targetY * Ex + targetZ;

注意单位为弧度。

第三步是空间直角坐标系转大地坐标系，转后的大地坐标系为80的大地坐标系，如图：

80、54、84坐标系七参数转换算法

其中a,b是西安80椭球长短轴，代码如下：

//第三步转换，空间直接坐标系转换为大地坐标系
private void XYZtoBLH(double X, double Y, double Z, double aAxis, double bAxis) {
double e1 = (Math.pow(aAxis, 2) - Math.pow(bAxis, 2)) / Math.pow(aAxis, 2);
double e2 = (Math.pow(aAxis, 2) - Math.pow(bAxis, 2)) / Math.pow(bAxis, 2);
double S = Math.sqrt(Math.pow(X, 2) + Math.pow(Y, 2));
double cosL = X / S;
double B = 0;
double L = 0;
L = Math.acos(cosL);
L = Math.abs(L);
double tanB = Z / S;
B = Math.atan(tanB);
double c = aAxis * aAxis / bAxis;
double preB0 = 0.0;
double ll = 0.0;
double N = 0.0;
//迭代计算纬度
do {
preB0 = B;
ll = Math.pow(Math.cos(B), 2) * e2;
N = c / Math.sqrt(1 + ll);
tanB = (Z + N * e1 * Math.sin(B)) / S;
B = Math.atan(tanB);
}
while (Math.abs(preB0 - B) >= 0.0000000001);
ll = Math.pow(Math.cos(B), 2) * e2;
N = c / Math.sqrt(1 + ll);
targetZ = Z / Math.sin(B) - N * (1 - e1);
targetB = B * 180 / Math.PI;
targetL = L * 180 / Math.PI;
}

第四步是进行高斯变换，将大地坐标转为平面坐标，公式如图：

80、54、84坐标系七参数转换算法

有点复杂，也一时说不清，具体可以查查高斯变换，这个还是很多的。代码如下：

//第四部转换，高斯变换，大地坐标系转平面坐标系，84转80
private void gaussBLtoXY(double mX,double mY){
double m_aAxis = Axis_WGS84_a; //参考椭球长半轴
double m_bAxis = Axis_WGS84_b; //参考椭球短半轴
double m_dbMidLongitude = transParaSeven.daihao*3;//中央子午线经度济南117 威海123 巴州 87
double m_xOffset = 500000;
double m_yOffset = 0.0;
try{
//角度到弧度的系数
double dblD2R = Math.PI / 180;
//代表e的平方
double e1 = (Math.pow(m_aAxis, 2) - Math.pow(m_bAxis, 2)) / Math.pow(m_aAxis, 2);
//代表e'的平方
double e2 = (Math.pow(m_aAxis, 2) - Math.pow(m_bAxis, 2)) / Math.pow(m_bAxis, 2);
//a0
double a0 = m_aAxis * (1 - e1) * (1.0 + (3.0 / 4.0) * e1 + (45.0 / 64.0) * Math.pow(e1, 2) + (175.0 / 256.0) * Math.pow(e1, 3) + (11025.0 / 16384.0) * Math.pow(e1, 4));
//a2
double a2 = -0.5 * m_aAxis * (1 - e1) * (3.0 / 4 * e1 + 60.0 / 64 * Math.pow(e1, 2) + 525.0 / 512.0 * Math.pow(e1, 3) + 17640.0 / 16384.0 * Math.pow(e1, 4));
//a4
double a4 = 0.25 * m_aAxis * (1 - e1) * (15.0 / 64 * Math.pow(e1, 2) + 210.0 / 512.0 * Math.pow(e1, 3) + 8820.0 / 16384.0 * Math.pow(e1, 4));
//a6
double a6 = (-1.0 / 6.0) * m_aAxis * (1 - e1) * (35.0 / 512.0 * Math.pow(e1, 3) + 2520.0 / 16384.0 * Math.pow(e1, 4));
//a8
double a8 = 0.125 * m_aAxis * (1 - e1) * (315.0 / 16384.0 * Math.pow(e1, 4));
////纬度转换为弧度表示
//B
double B = mX * dblD2R;
//l
double l = (mY - m_dbMidLongitude) * dblD2R;
////X
double X = a0 * B + a2 * Math.sin(2.0 * B) + a4 * Math.sin(4.0 * B) + a6 * Math.sin(6.0 * B) + a8 * Math.sin(8.0 * B);
//
double ll = Math.pow(Math.cos(B), 2) * e2;
double c = m_aAxis * m_aAxis / m_bAxis;
//N
double N = c / Math.sqrt(1 + ll);
//t
double t = Math.tan(B);
double p = Math.cos(B) * l;
double dby = X + N * t * (1 + ((5.0 - t * t + (9.0 + 4.0 * ll) * ll) + ((61.0 + (t * t - 58.0) * t * t + (9.0 - 11.0 * t * t) * 30.0 * ll) + (1385.0 + (-31111.0 + (543 - t * t) * t * t) * t * t) * p * p / 56.0) * p * p / 30.0) * p * p / 12.0) * p * p / 2.0;
double dbx;
dbx = N * (1.0 + ((1.0 - t * t + ll) + ((5.0 + t * t * (t * t - 18.0 - 58.0 * ll) + 14 * ll) + (61.0 + (-479.0 + (179.0 - t * t) * t * t) * t * t) * p * p / 42.0) * p * p / 20.0) * p * p / 6.0) * p;
mTargetX = dbx + m_xOffset;
mTargetY = dby + m_yOffset;
}
catch (Exception ex) {
}
}