❝

【GiantPandaCV导语】这是LeetCode第226场周赛题解，本周考察的知识点有枚举，贪心，前缀和，Manacher回文算法，动态规划，图论等。

❞

比赛链接

https://leetcode-cn.com/contest/weekly-contest-226/
最终Rank：231 / 4033。

题目一：盒子中小球的最大数量

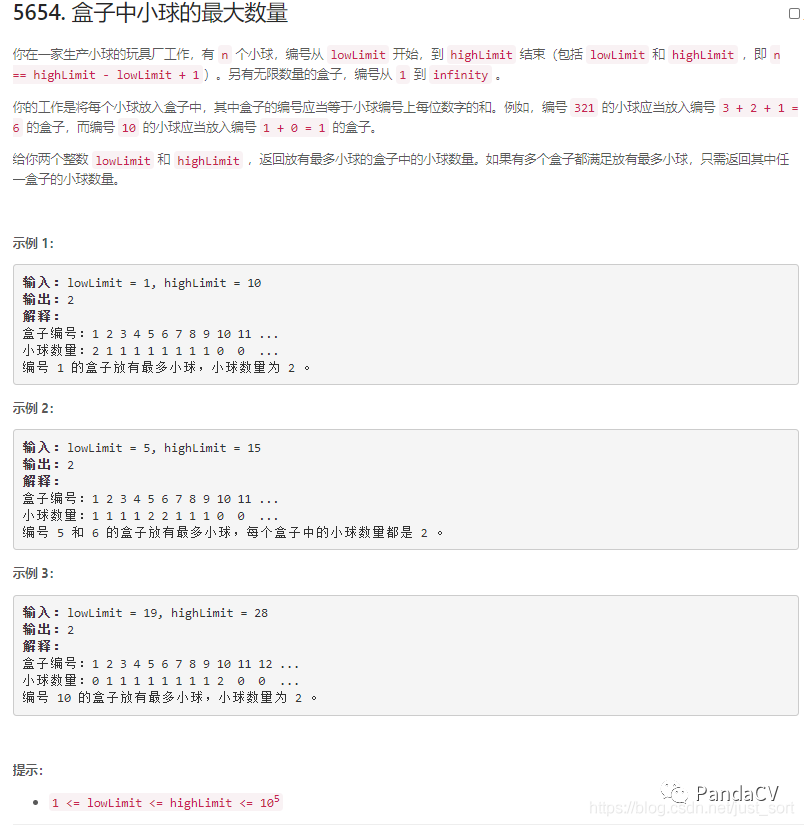
LeetCode 226场周赛题解

题面

解题思路：按照题意模拟一下即可。
时间复杂度：
空间复杂度：
解题代码如下：

class Solution { public: int a[100]; int f(int x){ int ans=0; while(x){ ans+=x%10; x/=10; } return ans; } int countBalls(int lowLimit, int highLimit) { int ans=0; for(int i=lowLimit; i<=highLimit; i++){ a[f(i)]++; } for(int i=1; i<100; i++){ if(a[i]>ans){ ans=a[i]; } } return ans; } };

题目二：从相邻元素对还原数组

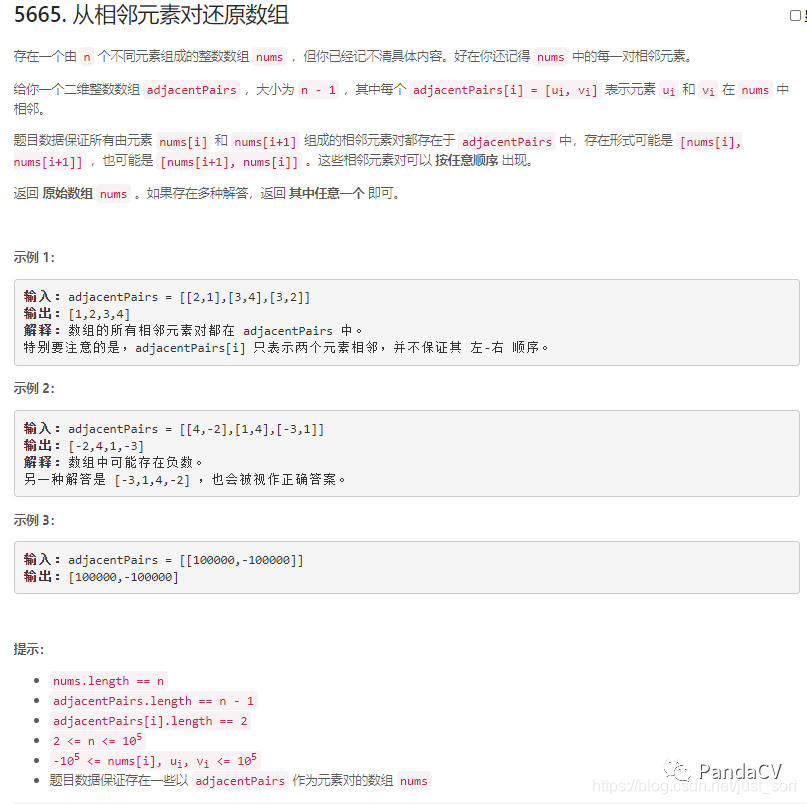
LeetCode 226场周赛题解

题面

解题思路：看了一分钟似乎没有思路？然后再想想我们会发现如果把这个相邻关系看成一个无向图的边这个图会是什么样子？其实这个图会退化成一条链，我们只需要找到这个链的头部或者尾部节点就可以一下把这个链拎起来，然后我们就获得了答案了。头部节点或者尾部节点怎么找？直接找入度或者出度为0的点就可以了。另外注意一下，图中节点可能是负数，所以需要加一个offset（我直接取了100000）来方便处理。
时间复杂度：
空间复杂度：
解题代码如下：

class Solution { public: int cnt[200010]; vector <int> G[200010]; vector <int> ans; void dfs(int root, int fa){ ans.push_back(root-100000); for(int i=0; i<G[root].size(); i++){ int v = G[root][i]; if(v == fa) continue; dfs(v, root); } } vector<int> restoreArray(vector<vector<int>>& adjacentPairs) { int n = adjacentPairs.size(); for(int i=0; i<n; i++){ int u = adjacentPairs[i][0]; int v = adjacentPairs[i][1]; u += 100000; v += 100000; G[u].push_back(v); G[v].push_back(u); cnt[v]++; cnt[u]++; } int id = 0; for(int i=0; i<200010; i++){ if(cnt[i]==1){ id = i; break; } } ans.clear(); dfs(id, -1); return ans; } };

题目三：你能在你最喜欢的那天吃到你最喜欢的糖果吗？

LeetCode 226场周赛题解

题面

解题思路：其实是一个非常简单的题目，只要推一下第一组样例应该就差不多了。对于每一个查询，我们可以O(1)判断是否可以在第 favoriteDayi天吃到 favoriteTypei类糖果。具体怎么判断呢？我们可以看到由于第二个条件的限制，在吃第类糖果的时候，那么类一定被吃掉了，那么我们可以i对所有的糖果维护一个前缀和。然后我们反向思考什么情况下这个人在第天是吃不到 favoriteTypei类苹果的：
一种情况就是这个人每天都吃了 dailyCapi（上限）这么多个苹果，但是还是不够数，也就是说 favoriteTypei类之前的苹果还有剩余。
另外一种情况就是这个人每天只吃一个苹果，但是到 favoriteDayi天吃的苹果数量（也就是天数）都已经超过了 favoriteTypei前所有的苹果数量，这样也是不行的。
时间复杂度：
空间复杂度：
解题代码如下：

class Solution { public: int n; long long sum[100010]; bool check(long long type, long long day, long long cap){ if(sum[type-1]>=(long long)(cap*day)) return false; if(day>sum[type]) return false; return true; } vector<bool> canEat(vector<int>& candiesCount, vector<vector<int>>& queries) { n = candiesCount.size(); for(int i=1; i<=n; i++){ sum[i]=sum[i-1]+candiesCount[i-1]; } vector<bool>ans; for(int i=0; i<queries.size(); i++){ long long type = queries[i][0]; long long day = queries[i][1]; long long cap = queries[i][2]; type++; day++; if(check(type, day, cap)){ ans.push_back(true); } else{ ans.push_back(false); } } return ans; } };

题目四：回文串分割 IV

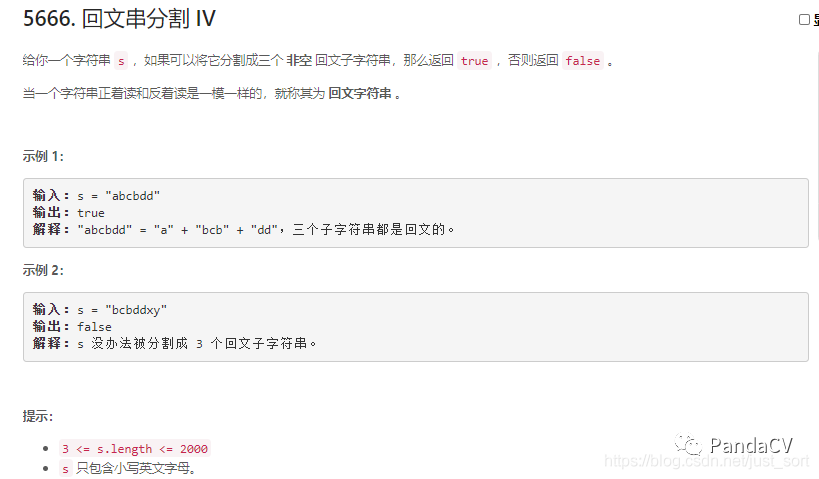
LeetCode 226场周赛题解

题面

解题思路：这道题其实有两种解法，一种是适合本地2e3的数据范围，一种是适合2e4的数据范围，接下来我就讲一下这两种做法。

解题方法一：O(n^2) DP

解题思路：这是针对本题的数据范围的一种解法，我们设 dp[i][j]表示字符串中的这一段字串是否是回文串，我们可以从后往前枚举字串的起点进行DP方程状态的更新。维护完这个数组之后我们就可以枚举第一个子段的终点和第二个子段的起点来判断获得最终答案了。
时间复杂度：
空间复杂度：
解题代码：

class Solution { public: bool checkPartitioning(string s) { int n = s.length(); vector<vector<bool>> p(n, vector<bool>(n)); for (int i = n - 1; i >= 0; --i) { p[i][i] = true; for (int j = i + 1; j < n; ++j) { if (s[i] == s[j]) { p[i][j] = (i + 1 == j || p[i + 1][j - 1]); } } } for (int i = 0; i < n; ++i) { if (p[0][i]) { for (int j = i + 1; j < n - 1; ++j) { if (p[i + 1][j] && p[j + 1][n - 1]) { return true; } } } } return false; } };

解题方法二：枚举+Manacher

解题思路：先用Manacher算法得到以每个点为中心的最大回文串的左右边界 le[i]、 ri[i]。并且当 le[i]==1（即该回文串向左可以到达字符串的边界）时，记录下来， le1[ri[i]]=1，表示存在一个回文串左边界为1，右边界为 ri[i]。同理，当 ri[i]==n-1（字符串右边界）时， ri1[le[i]]=1。然后遍历中间的回文串的回文中心，令 t1=p[i]-1（回文串长度）， t2=le[i]（回文串左边界）， t3=ri[i]（回文串右边界），当 le1[t2]==1&& ri1[t3]==1时即找到了方案。如果不满足， t1-=2，t2+=2，t3-=2，继续判断，直到 t1<=0。要注意的是当 t2==1或者 t3==n-1时该回文串不能作为中间回文串。关于Manacher算法不了解的读者请看： https://oi-wiki.org/string/manacher/
时间复杂度：
空间复杂度：
解题代码：

`const int maxn=2e3+5;
int T,n,ans,p[maxn<<1],le[maxn<<1],ri[maxn<<1];
int le1[maxn<<1],ri1[maxn<<1];
char s[maxn<<1],ss[maxn];

void manacher(){
    int mid=0,r=0;
    for(int i=1;i<n;++i){
        if(r>=i) p[i]=min(p[(mid<<1)-i],r-i+1);
        while(s[i-p[i]]==s[i+p[i]]) ++p[i];
        if(i+p[i]>r) r=i+p[i]-1,mid=i;
        int tmp=p[i]-1;
        le[i]=i-tmp,ri[i]=i+tmp;
        if(le[i]==1) le1[ri[i]]=1;
        if(ri[i]==n-1) ri1[le[i]]=1;
    }
}

class Solution {
public:
    bool checkPartitioning(string s2) {
        ans = 0;
        n = s2.size();
        for(int i=0; i<n; i++) ss[i]=s2[i];

        s[0]='~',s[1]='|';
        for(int i=0;i<n;++i)
            s[2*i+2]=ss[i],s[2*i+3]='|';
        n=2*n+2;
        for(int i=0;i<n;++i)
            p[i]=0,le1[i]=0,ri1[i]=0;
        manacher();
        for(int i=1;i<n;++i){
            int t1=p[i]-1,t2=le[i],t3=ri[i];
            if(t2==1||t3==n-1){
                t1-=2;
                t2+=2;
                t3-=2;
            }
            while(t1>0){
                if(le1[t2]&&ri1[t3]){
                    ans=1;
                    break;
                }
                t1-=2;
                t2+=2;
                t3-=2;
            }
            if(ans) break;
        }
        if(ans) return true;
        else return false;
    }
};
`