憋了两周多这个算法算是憋出来了。大体思路是通过 parser 解析表达式,产生一颗 AST 树。然后将 AST 编译成指令序列。
举个例子:12 + 12 * 2 - 12,根据先算乘除后算加减的规则表达式要被编译成:12,12,2,*,+,12,- 。这个编译结果被执行的过程是如下这样:
- 会入栈 三个数:12,12,2
- 执行乘法操作,乘法操作会消耗两个栈顶数据然后产生一个新的栈数据,结果为:12,24
- 执行加法操作,消耗了栈上的两个数据,产生了一个新数据,最后栈上的数据为 36
- 接着入栈12,栈上的数据为,36,12
- 在执行减法,操作,消耗两个栈数据产生一个新数据:24
在这个例子里首先要把表表达式编译成 AST 树,如下:
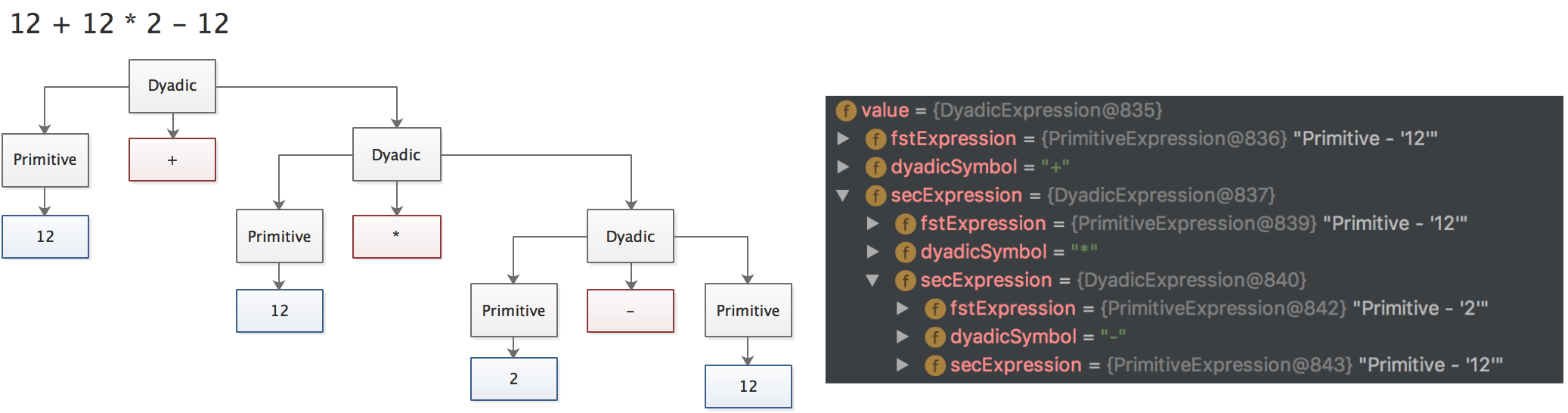
DataQL 的算法是独创的(未经调研市面上或许有相似的算法),首先DataQL 在处理二元表达式编译时表达式一定是可以被简化为上述形态(一颗右偏的 AST 树)这种树的好处是使用任何一个语法解析器都非常容易生成,而且您也不需要额外了解多少编译原理的基础知识。
DataQL 就是使用 javacc 生成这样的一棵树,花在这方面的代码大致如下:
// .表达式 = 表达式 or 表达式 + 运算符
Expression expression() : { Expression exp;
} {
(
// 括号优先级
<OPAR> exp = expression() <CPAR> {exp = new PrivilegeExpression(exp);}
(
exp = extExpression(exp)
)? {return exp;}
) | (
exp = basicValue()
(
exp = dyadicExpression(exp)
)? {return exp;}
)
}
DyadicExpression dyadicExpression(Expression fstExp) : {
Token symbol = null;
Expression secExp = null;
} {
(
symbol = <PLUS>
| symbol = <MINUS>
| symbol = <STAR>
| symbol = <SLASH>
| symbol = <REM>
| symbol = <ALI>
| symbol = <GT>
| symbol = <GE>
| symbol = <LT>
......
| symbol = <SC_OR>
| symbol = <SC_AND>
)
secExp = expression() {return new DyadicExpression(fstExp,symbol.image,secExp);}
}
我们可以看到在处理括号时,总是会以 PrivilegeExpression 类型作为一层包装。平时一般的带有符号的表达式计算都是以 DyadicExpression 作为载体。
因此如下两个带有括号的表达式在编译成 AST 树时大概类似这个样子(一棵看上去非右偏的树):
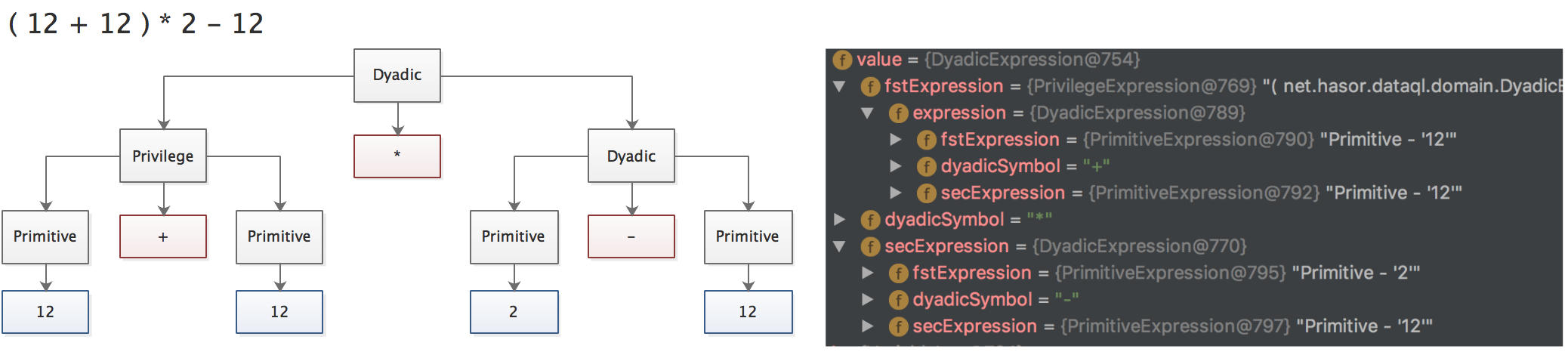
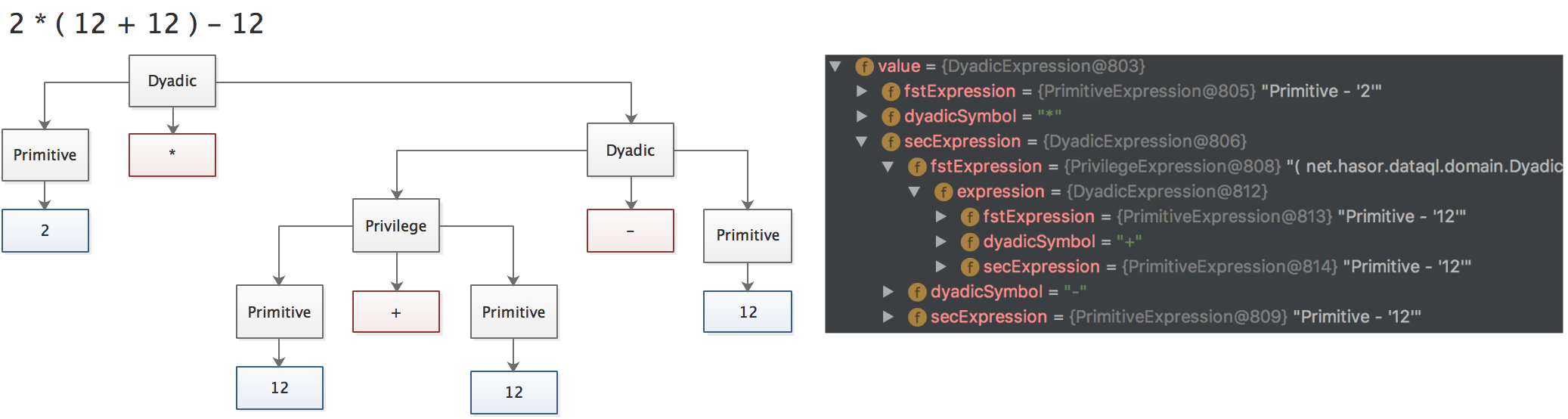
现在 我们来回想一下当计算带有括号的表达式时,如果把括号的里面的表达式单独提出来就会是这个样子:( 12 + 12 ) * 2 - 12 -> a = 12 + 12 , reslt = a * 2 - 12。
现在分别在看这两个表达式它们又回到了右偏的状态,所以带有括号的表达式是可以被拆解为多个右偏 AST 树的。这个拆解的节点就是 PrivilegeExpression。
好了讨论到这里,我们已经把带有括号的表达式编译拆解成为对一棵右偏树的编译。现在让我们继续看这个例子:

我们看到每一个 D(DyadicExpression) 节点,都有两个运算表达式和一个操作符。我们把写法简化一下至少看上去比较简洁:
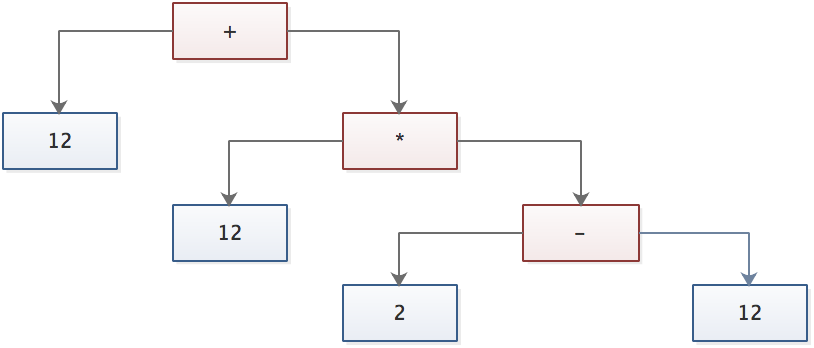
表达式的编译是在每个 D 节点上进行,在上图中 D 节点就是红色部分由运算符表示的节点。
在正式介绍算法逻辑之前,我们先为这课右偏树做编码
轮数
助记符
1
+,12
2
*,12
3
-,2
E
12
算法需要一个后进先出(LIFO)数据结构,这个数据结构是用于帮助我们有效的处理运算符在合理位置上被编译出去。我们用 last 变量表示这个结构。同时 self 表示当前运算符,next表示下一个运算符。
算法中每一轮都要输出它对应助记符上的操作数。另外第一轮和最后一轮计算比较特殊,我们安顺序先看第一轮。
第一轮:
第一轮的标准是 last 中是否为空,如果为空则表示这是第一轮计算。
在第一轮计算中非常简单,只需要输出编码表中的操作数。在这个例子中只需要输出 12。然后把操作符添加到 last 中。
此时编译结果为:12,last的值为:+
第二轮:
第二轮开始之前会先输出第二轮的操作数,12。这时编译结果为:12,12。
接着我们判断当前节点的操作符优先级是否小于等于 last 栈顶的操作符,即:“*” <= “+”
我们知道乘法的优先级要比加法高,因此判断结果为 false。
如果判断结果为 fasle,那么就把 self 添加到 last 中。然后结束。
此时编译结果为:12,12,last的值为:+,*
第三轮:
第三轮开始之前会先输出第二轮的操作数,2。这时编译结果为:12,12,2
接着我们判断当前节点的操作符优先级是否小于等于 last 栈顶的操作符,即:“-” <= “*”
我们知道减法的优先级没有乘法高,因此判断结果为 true。
如果判断结果为 true,那么就进入一个循环。
循环里,首先执行 list 的出栈操作。把出栈的操作符输出到编译结果中。然后在开始下一轮循环。
每一轮循环要做的事情都是,判断 self 是否小于等于 last 栈顶的操作符。当遇到 last 为空或者判断不为 true 时跳出循环。在这个例子中,每次循环的判断结果如下:
第一次:“-” <= “*” = true,输出栈顶操作符 “*”,编译结果为:12,12,2,*,last的值为:+
第二次:“-” <= “+” = true,输出栈顶操作符 “*”,编译结果为:12,12,2,*,+,last的值为:空
第三次:因为 last 为空,所以跳出循环。
最后一步,把 self 追加到 last中。
此时编译结果为:12,12,2,*,+,last的值为:-
第E轮:
E轮是最后一轮,当节点的第二个操作数不是 D 类型时表示是E轮。在 E 轮中,self 是没有值的因此 E轮的处理逻辑通常是跟随在 E 轮前面的那一轮表达式编译计算节点中。启用 E 轮的依据就是 next 是否为空。如果为空表示启动 E 轮的逻辑。
在 E 轮中首先输出第二个表达式。
然后进入一个循环,每次循环都把 last 做出站操作并输出操作符。直到 last 为空。结束 E 轮。
在这个例子中,循环只会走一次,最后的编译结果为:12,12,2,*,+,12,-
结论:
12,12,2,*,+,12,- 这个编译结果和我们预期的要求完全一致,在最后贴上算法的完整逻辑:
put fstExpression
if last = empty then
goto self
end
while last.empty = false
//根据优先级Tab,计算 slef 的运算符是否比 last 中最后一个放进去的优先级要低
if self <= last.peek then
put last.pop
else
goto self
end
end
self : last.push( self )
if next = null then
put secExpression
while last.empty = false
put last.pop
end
end
使用这种算法来处理带有优先级的表达式编译有一个很大的好处就是:你如果需要调整运算符优先级只需要调整 运算符优先级tab 中的数据就可以。 从而避免了在 词法分析时为了优先级而去设计 AST 解析树的解析机制。
最后附上 DataQL 的表达式优先级tab:
// 优先级:
// 0st: () 括号
// 1st: -> 取值
// 2st: ! , ++ , -- 一元操作
// 3st: * , / , \ , % 乘除法
// 4st: + , - 加减法
// 5st: & , | , ^ , << , >> , >>> 位运算
// 6st: > , >= , == , != , <= , < 比较运算
// 7st: && , || 逻辑运算
DataQL的项目介绍和源码在这里:













