$Splay$的复杂度分析
不论插入,删除还是访问,我们可以发现它们的复杂度都和$splay$操作的复杂度同阶,只是一点常数的区别
我们不妨假设有$n$个点的$splay$,进行了$m$次$splay$操作
采用势能分析
我们记$w(x) = \left \lceil \log_2 (size(x)) \right \rceil$,注意以$2$为底和上取整
我们定义势能函数为$\varphi = \sum w(x)$
(记第$i$次操作操作完之后,势能为$\varphi(i)$)
只需要估计出$\varphi(m) - \varphi(m - 1) + \varphi(m - 1) - \varphi(m - 2) ... + \varphi(1) - \varphi(0) + \varphi(0)$的大小即可
(即初始势能和每次的势能变化量的和)
显然,$\varphi(0) \leqslant n \log n$
$splay$操作的具体定义为:
如果父节点是根,那么旋转一次
如果父节点和爷节点所处子树方向一致,那么先旋转父亲再旋转自己
否则,旋转两次自己
实际上可以归结于$zig$,$zag$,$zig-zig$,$zag-zag$,$zig-zag$,$zag-zig$操作
由于$zig$和$zag$是对称的操作
因此,只需要对$zig$,$zig-zig$,$zig-zag$操作分析复杂度即可
$zig$操作
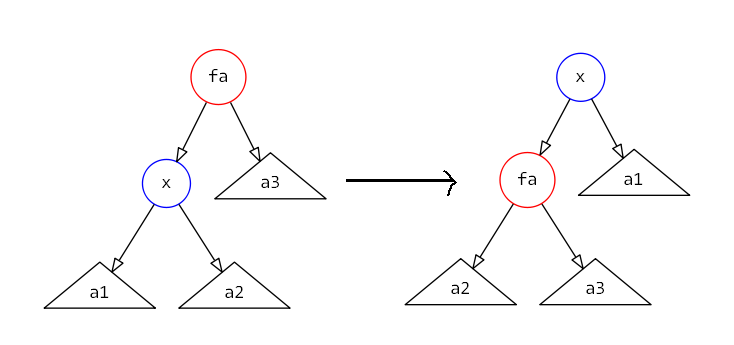
势能的变化量为$1 + w'(x) + w'(fa) - w(x) - w(fa) \leq 1 + w'(fa) - w(x) \leq 1 + w'(x) - w(x)$
$zig-zig$操作
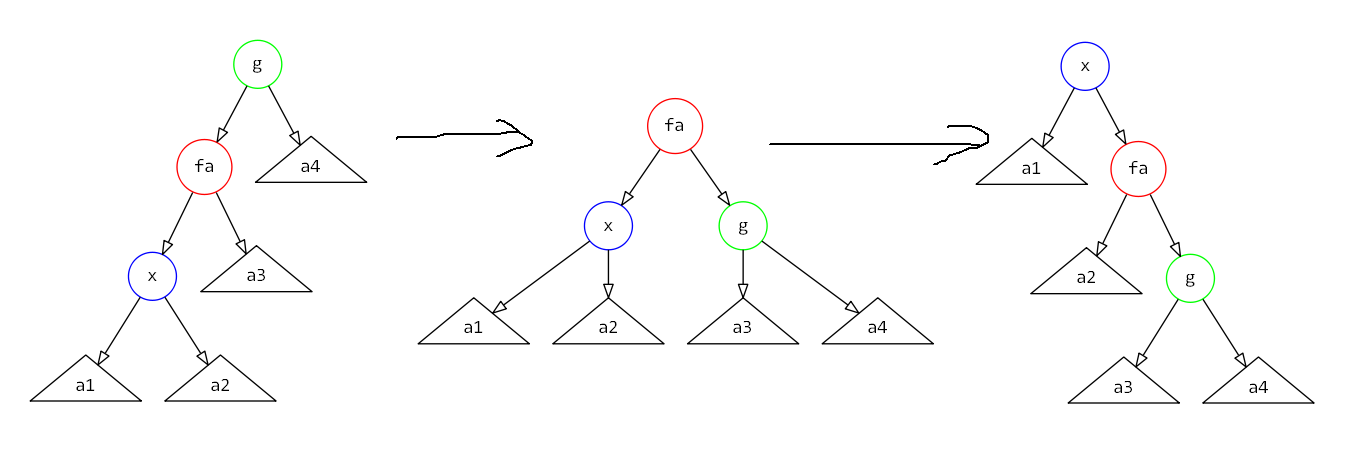
势能变化量为$1 + w'(x) + w'(fa) + w'(g) - w(x) - w(fa) - w(g)$(缩小了常数的影响,但不能无视)
$\leq 1 + w'(fa) + w'(g) - w(x) - w(fa) \leq 1 + w'(x) + w'(g) - 2w(x)$
这是神仙复杂度证明中非常神奇的地方,通过一些有趣的性质,让常数项的代价合并到了势能的变化中
我们不妨设$a = w'(g), b = w(x)$,那么注意到$w'(x) = a + b + 1$
由于$2w'(x) - w'(g) - w(x) = \left \lceil \log_2 (a + b + 1) \right \rceil - \left \lceil \log_2 a \right \rceil + \left \lceil \log_2 a + b + 1 \right \rceil - \left \lceil \log_2 b \right \rceil $
注意到$a, b$在上式中是对称的,不妨设$a \geq b$
$\geq \left \lceil \log_2 (a + b + 1) \right \rceil - \left \lceil \log_2 b \right \rceil \geq \left \lceil \log_2 (2b + 1) \right \rceil - \left \lceil \log_2 b \right \rceil \geq \left \lceil \log_2 b \right \rceil + 1 - \left \lceil \log_2 b \right \rceil \geq 1$
因此有$1 \leq 2w'(x) - w'(g) - w(x)$,我们将$1 + w'(x) + w'(g) - 2w(x)$中的$1$放缩,可以得到
$\leq 3(w'(x) - w(x))$
$zig-zag$操作
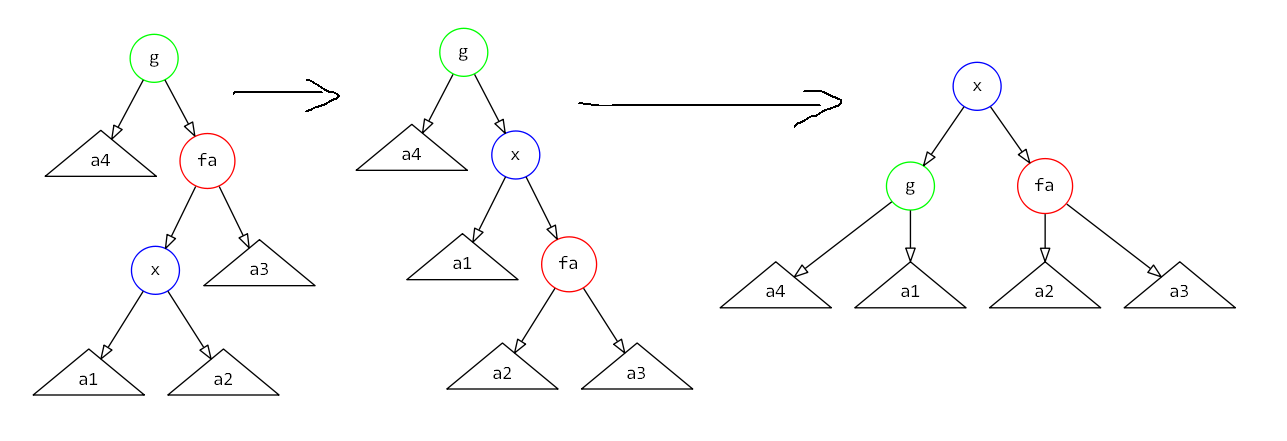
势能变化量为$1 + w'(x) + w'(fa) + w'(g) - w(x) - w(fa) - w(g) \leq 1 + w'(fa) + w'(g) - w(x) - w(fa) \leq 1 + w'(g) + w'(fa) - 2w(x)$
由上文的结论,我们知道这里可以把$1$放缩成$1 \leq 2w'(x) - w'(g) - w'(fa)$
因此$\leq 2(w'(x) - w(x))$
把以上三种操作的势能全部放缩为$\leq 3(w'(x) - w(x))$
不妨假设$splay$一次,依次访问了点$x_1, x_2 ... x_n$,最后$x_1$会成为新的根
那么,最后的势能实际上是$3(w'(x_1) - w(x_1) + w''(x_1) - w'(x_1) + .... + w(n) - w^{'''.....}(x_1)) + 1 = 3 * (w(n) - w(x_1)) + 1\leq log_2 n$
因此,$\varphi(m) - \varphi(m - 1) + \varphi(m - 1) - \varphi(m - 2) ... + \varphi(1) - \varphi(0) + \varphi(0) = n \log n + m \log n$
即$n$个点的$splay$,做$m$次$splay$操作,复杂度为$O(n \log n + m \log n)$
$LCT$的复杂度分析
不咕了....
$LCT$的所有操作可以看做只有$access$操作,其他都是常数
那么$access$操作一共有两部分
在$splay$中走的复杂度
访问虚边的复杂度
首先是在$splay$中走的复杂度
定义$w(x) = \left \lceil \log_2 (size(x)) \right \rceil$,$size(x)$指$x$的所有虚边和实边的子树大小的和
我们定义势能函数为$\varphi = \sum w(x)$
不妨设它依次访问了$x_1, x_2 ..., x_p$
那么,类似上文$splay$的复杂度分析,我们可以得到总的一次势能变化量为$-w(x_1) +w(x_2) - w(x_2) + w(x_3) ... +w(x_p) + 1\leq w(x_p) + 1 = O(\log n)$
这也就是$splay$的$finger-search$的性质
初始势能为$n \log n$,因此这一部分的复杂度为$O(n\log n + m \log n)$
访问虚边的复杂度
我们定义势能函数$\phi$,为所有重虚边(儿子的子树大小大于等于自己的二分之一的虚边)的数量
那么,每次访问至多走$\log$条轻虚边,也就至多带来$\log$条重虚边,也就是以$O(\log)$的代价增加$\log$的势能
而每次访问一条重虚边就需要付出$O(1)$的代价来减小$1$的势能,并且访问完重虚边之后,不会有新的重虚边产生
因此,最终的复杂度是初始势能和势能变化量(实际操作的代价和势能变化量相同)的和,也就是$O(n + m \log n)$
因此,$LCT$的复杂度为$O(n \log n + m \log n)$