一、二叉堆含义及属性:
堆(heap)亦被称为:优先队列(priority queue),是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。在队列中,调度程序反复提取队列中第一个作业并运行,因而实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。同垃圾收集存储的堆含义不同。
表示堆的数组A有两个属性:
A.length : 代表A数组的元素个数;
A.heapsize : 代表A数组中 属于堆元素个数。有时候(排序时),数组A的部分元素不属于堆。刚开始建堆的是偶,A.heapsize = A.length,排序时,每次从堆顶取出最大值,A.heapsize递减,直至排序完成.
下图是一个建好后的二叉堆:

从图中可知,已知某节点的索引值i,可以轻松获取其对应父节点,左,右子节点的索引值。有:
Parent(i)
return i/2; 或者 return i >> 1;
Left(i)
return i*2; 或者 return i << 1;
Right(i)
return i*2+1; 或者 return (i << 1) + 1;
二叉堆分两种: 最大堆,最小堆,均遵循堆属性。最大堆,每个节点i满足:
A[Parent(i)] ≥ A[i]
最小堆与之相反,每个节点i满足:
A[Parent(i)] ≤ A[i]
堆排序算法,我们用的是最大堆,因为最小堆用于实现优先队列(priority queues).二叉堆的其他属性同二叉树属性类似,如节点高度,树高度等。如n个元素的完全二叉树,树高为lgn, 故n个元素的二叉堆高度为lgn.
二、保持堆属性:
保持堆属性,或者称"大堆化", 关键函数是Max-Heapify, 构造二叉堆,以及二叉堆排序均需要调用该函数,如从无序数组构造二叉堆,就需要使所有节点"大堆化".

Max-Heapify 运行时间为O(h),h为对应节点高度.
伪代码分析:
到line 8,已经确定A[i], A[i].left, A[i].right 三者中最大值。如果最大值是根节点A[i],满足大堆属性,不需修改;反之, 则需把根节点同子节点中最大节点交换,同时因为最大子节点替换成比其值小的父节点,需要确保以该子节点为父节点的子树是否满足大堆属性,所以需要用largest 作为新i递归调用Max-Heapify.下图是一个 Max-Heapify 处理实例:

三、建堆
我们自底向上的用Max-Heapify 将无序数组A[1...n]转换成一个最大堆。因为二叉堆是完美二叉树,可知子序列A[(n/2+1)...n]中的元素均是叶子节点,每个都可以看成是一个元素的堆, 默认就满足堆属性。
BUILD-MAX-HEAP 对树中剩余所有非叶子节点调用 Max-Heapify,以维持堆属性。
BUILD-MAX-HEAP运行时间为O(n)。
下图是无序数组建堆示例图:
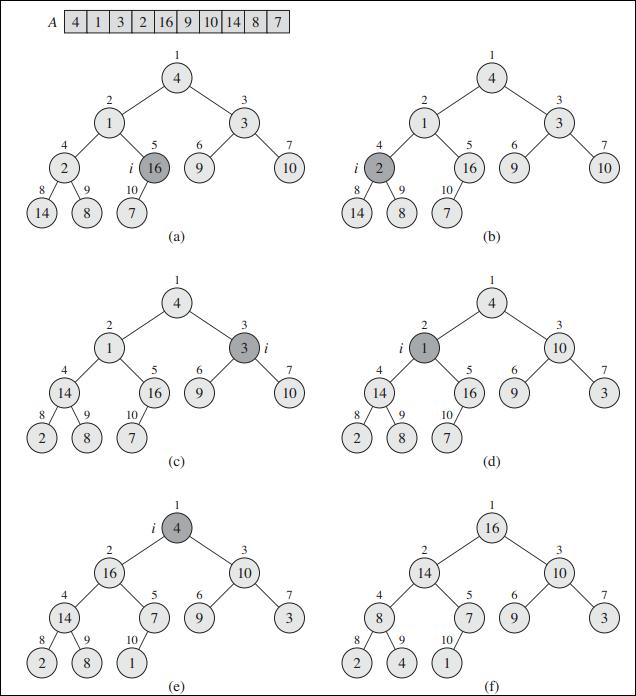
四、堆排序
接下来就是堆排序的实现了,通过BUILD-MAX-HEAP 建立大堆后,最大的元素在root,即A[0].可以先提取出该最大值,HeapSort首先把A[0]同A[n-1]交换,然后通过减小A.heap_size 来将最后一个元素a[n-1]移出堆。这样我们就获取了一个最大值。同时可以知道除了新的根节点,其他节点原来均保持堆属性,为恢复堆属性,我们调用Max-Heapify(A,0),以让以A[0]为根节点的堆保持堆属性.接下来重复该过程,每次移除最大节点(root节点),可以完成排序操作。

下图是构建大堆后,堆排序的示例图:

HeapSort 运行时间为O(nlgn).有堆排序的平均时间复杂度为O(nlgn),空间复杂度为O(1)。
五、优先级队列(priority queue)
作为排序算法,实际中快排比堆排序更加有效。但二叉堆有别的用处,如高效的优先级队列。同二叉堆一样,优先级队列也分两种: 最大优先级队列,最小优先级队列。
优先级队列作为管理一组数据集合S的数据结构,支持以下操作:
Insert(S,x) 将新元素插入集合S中。
Maximum(S) 返回集合S中最大元素。
Extract-Max(S) 从集合S中移除最大元素,并返回。
Increase-Key(S,x,key) 将集合S中x位置元素值替换成key,这里假定新key值不能小于x原来位置值,主要用来Insert时调用,新增空节点,并赋予新key值。
最大优先级队列用于在分时系统中进行作业调度。队列对将要执行的作业和作业优先级做记录。当一个作业完成或者中断了,用Extract-Max 从所有待运行作业中,取出最高优先级作业。任何时候加入新作业,可以使用Insert 加入队列中。
相应的,最小优先级队列支持Insert,Minimum,Extract-Min,Decrease-Key等操作。主要用于事件驱动模拟器中。
1、Heap-Extract-Max 伪代码如下,类似于Heapsort for循环部分:

Heap-Extract-Max 运行时间为O(lgn).
2、Heap-increase-key 伪代码如下,因为把key值赋予(如新创建的空)i节点,可能会破坏堆属性,所有line 4的while循环用于恢复堆属性。

Heap-increase-key 运行时间为O(lgn).
3、Max-Heap-insert伪代码如下:

Max-Heap-insert 运行时间为O(lgn). 可知,n个节点的二叉堆,优先级队列所有操作时间均为O(lng).
六、二叉堆其他应用:
1、C++中的STL 已经实现了优先队列 priority_queue, 网上也很多文章介绍如何使用。
2、哈夫曼编码。
3、一些任务调度算法。
4、一个修改版的堆排:每次不是将堆底的元素拿到上面去,而是直接比较堆顶(最大)元素的两个儿子,即选出次大的元素。由于这两个儿子之间的大小关系是很不确定的,两者都很大,说不好哪个更大哪个更小,所以这次比较的两个结果就是概率均等的了。具体参考这里。
code:因为使用了C++类,破坏了堆排序的原地性,但是原理不变,同时代码中也有提示~
/*************************************************************************
* heap sort algorithm and priority queue .
* Date : 28/07/2014
* author : alex xiao
* tips :
* 1. Two different way to build a binary heap(priority queue), max_heap_insert and
* build_max_heap. no need call together.
* 2. heap_extract_max can't call with heap_sort at the same time, as m_heap_size decrease.
* 3. heap sort no need use C++ class, destory in place property. you can replace m_array with
* array, replace m_length with array_length.
*************************************************************************/
#include <iostream>
#include <time.h>
#include <stdlib.h>
using namespace std;
template<typename T>
class binary_heap
{
public:
binary_heap() : m_array(NULL), m_length(0), m_max_size(0) m_heap_size(0)
{}
binary_heap(int length);
~binary_heap(void)
{
delete [] m_array;
}
void build_max_heap(T * array, int array_length);
void heap_sort(T * array, int array_length);
void maxHeapify(T * array, int n);
void heap_dump(void);
int heap_maximum(void);
int heap_extract_max(void);
int heap_increase_key(int i, T key);
int max_heap_insert(T key);
private:
T* m_array;
int m_length;
int m_max_size;
int m_heap_size;
};
int main(void)
{
int i = 0;
int array[10] = {4, 1, 3, 2, 16, 9, 10, 14, 8, 7};
int array_length = sizeof(array)/sizeof(array[0]);
binary_heap<int> bh(array_length);
for(i = 0; i < array_length; i++)
{
bh.max_heap_insert(array[i]);
}
cout << "Before sort : " << endl;
bh.heap_dump();
bh.heap_sort(array, array_length);
return 0;
}
template<typename T>
binary_heap<T>::binary_heap(int length)
{
m_array = new T[length];
m_length = 0;
m_heap_size = 0;
m_max_size = length;
}
/******************************************************************************
* runs in O(lgn) time, sorts an array in place.
* tips: heap sort no need use C++ class, destory in place property. you can replace m_array with
* array, replace m_length with array_length.
******************************************************************************/
template<typename T>
void binary_heap<T>::heap_sort(T * array, int array_length)
{
int i = 0;
int heap_size = m_length;
build_max_heap(m_array, m_length);
cout << "After build_max_heap : " << endl;
heap_dump();
for(i = m_length-1; i>=0; i--)//数组中下标从0 - n-1
{
int temp = m_array[0];
m_array[0] = m_array[i];
m_array[i] = temp;
m_heap_size--;
maxHeapify(m_array, 1);//在堆中,堆顶元素下标从1开始
}
cout << "After Sort : " << endl;
heap_dump();
}
/******************************************************************************
* runs in linear time, produces a max-heap from an unordered input array
******************************************************************************/
template<typename T>
void binary_heap<T>::build_max_heap(T * array, int array_length)
{
int i = 0;
m_heap_size = array_length;
for(i = array_length/2 ; i>=1 ; i--)//注意i的取值,堆的高度从1 - n/2
{
maxHeapify(array, i);
}
}
/******************************************************************************
* runs in O(lgn) time, the key to maintaining the max-heap property.
******************************************************************************/
template<typename T>
void binary_heap<T>::maxHeapify(T * array, int temp)
{
int largest = 0;//以temp为顶点的子树的堆顶
int l = temp << 1;//求以temp为顶点的子树左儿子
int r = (temp << 1) + 1;//求以temp为顶点的子树右儿子
if(l <= m_heap_size && array[l-1] > array[temp-1])//首先判断左儿子是否存在,即l<=heap_size
{
largest = l;
}
else
{
largest = temp;
}
if(r <= m_heap_size && array[r-1] > array[largest-1])//首先判断右儿子是否存在,即r<=heap_size
{
largest = r;
}
if(largest != temp)
{
int t = array[temp-1];
array[temp-1] = array[largest-1];
array[largest-1] = t;
maxHeapify(array, largest);//调整为大顶堆
}
}
/******************************************************************************
* returns the element of A with the largest key.
******************************************************************************/
template<typename T>
int binary_heap<T>::heap_maximum(void)
{
if(m_length < 1)
{
cout << "array underflow !" << endl;
return -1;
}
return m_array[0];
}
/******************************************************************************
* removes and returns the element of A with the largest key.
* Roughly same with heap_sort if extract all nodes.
* Can't call with heap_sort at the same time, as m_heap_size will decrease.
******************************************************************************/
template<typename T>
int binary_heap<T>::heap_extract_max(void)
{
int max = 0;
if(m_heap_size < 1)
{
cout << "array underflow !" << endl;
return -1;
}
max = m_array[0];
m_array[0] = m_array[m_heap_size -1];
m_heap_size--;
maxHeapify(m_array, 0);
return max;
}
/******************************************************************************
* increases the value of element i's key to the new value key, which is assumed to be at least
* as large as i's current key value.
* repeatedly compares an element to its parent, exchanging their keys and continuing if the
* element's key is larger, and terminating if the element's key is smaller, since the max-heap
* property now holds.
* roughly same with maxHeapify.
******************************************************************************/
template<typename T>
int binary_heap<T>::heap_increase_key(int i, T key)
{
int tmp = 0;
int parent = i >> 1;
if(key < m_array[i-1])
{
cout << "new key is smaller than current key." << endl;
return 0;
}
m_array[i-1] = key;
while( (i >= 1) && (parent >= 1) && (m_array[parent-1] < m_array[i-1]) )
{
tmp = m_array[i-1];
m_array[i-1] = m_array[parent-1];
m_array[parent-1] = tmp;
i = parent;
parent = i >> 1;
}
return 0;
}
/******************************************************************************
* INSERT operation.The procedure first expands the max-heap by adding to the tree a new leaf
* whose key is -1. Then it calls HEAP-INCREASE-KEY to set the key of this new node to its
* correct value and maintain the max-heap property.
* roughly same with build_max_heap.
******************************************************************************/
template<typename T>
int binary_heap<T>::max_heap_insert(T key)
{
m_length++;
m_heap_size++;
if(m_max_size < m_length)
{
cout << "max heap is overflow ~" << endl;
return -1;
}
m_array[m_heap_size-1] = -1;
heap_increase_key(m_heap_size, key);
return 0;
}
/******************************************************************************
* just for test, dump array infor
******************************************************************************/
template<typename T>
void binary_heap<T>::heap_dump(void)
{
int i = 0;
for(i = 0; i < m_length; i++)
{
cout << m_array[i] << " ";
}
cout << endl;
}
待优化的地方有:
1、在进行堆排序时,每次取出堆顶元素,用最后一个元素替换成新堆顶,这时新堆顶明显会小于之前堆顶的两个子节点,所以是必然需要调整堆,会浪费不少时间,可以优化成从原来堆顶两个子节点中选取最大值作为新堆顶。
有任何问题,还请不吝指出谢谢~
reference:
Introduction to algorithms(算法导论第三版)
http://zh.wikipedia.org/wiki/%E5%A0%86%E6%8E%92%E5%BA%8F
http://zh.wikipedia.org/wiki/%E5%A0%86\_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84)













