给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1输出：tail connects to node index 1解释：链表中有一个环，其尾部连接到第二个节点。

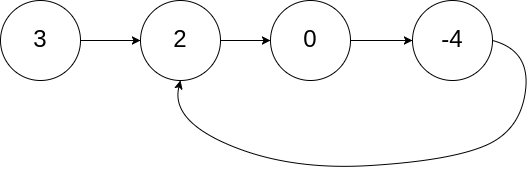
示例 2：

输入：head = [1,2], pos = 0输出：tail connects to node index 0解释：链表中有一个环，其尾部连接到第一个节点。

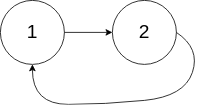
示例 3：

输入：head = [1], pos = -1输出：no cycle解释：链表中没有环。

链表结构

1class ListNode {2    int val;3    ListNode next;45    ListNode(int x) {6        val = x;7        next = null;8    }9}

答案：

 1public ListNode detectCycle(ListNode head) { 2    if (head == null || head.next == null || head.next.next == null) 3        return null; 4    ListNode slow = head.next; 5    ListNode fast = head.next.next; 6    while (slow != fast) { 7        if (fast.next == null || fast.next.next == null) 8            return null; 9        slow = slow.next;10        fast = fast.next.next;11    }12    slow = head;13    while (slow != fast) {14        slow = slow.next;15        fast = fast.next;16    }17    return slow;18}

解析：

首先通过快慢指针判断链表是否有环，如果没环则返回null，如果有环肯定会在环中的某一点相遇，在相遇的时候快指针从相遇的那一刻开始，慢指针从头开始，每次都只走一步，再次相遇的时候就是环的入口。画个图来分析一下更有助于理解。

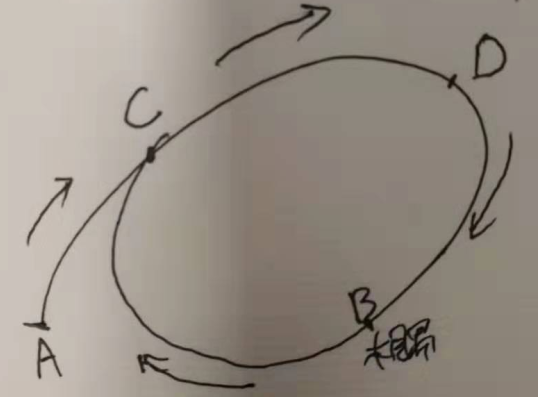
我们假设链表有环。快慢指针都从A开始沿着箭头方向出发，假如快慢指针在B点相遇，那么慢指针走过的路径是A->C->D->B,如果把链表完整走完一次就差B->C这段路径了。快指针走过的路径是A->C->D->B->C->D-B,如果把链表完整走完两次就差B->C这段和A->C这段路径了，所以我们可以得出A->C等于B->C，即C点就是环的入口。关于链表是否有环我们还可以参照以前的一道题141， 环形链表

本文分享自微信公众号 - 数据结构和算法（sjjghsf）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。